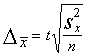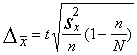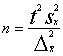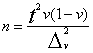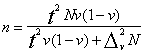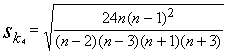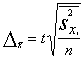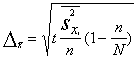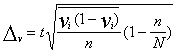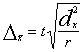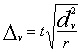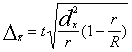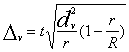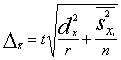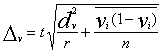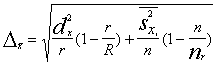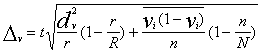5. Izlases metode

 

5.1. Uzdevuma nostādne, pamatjēdzieni un apzīmējumi.

 

            Statistiski novērojamie objekti parasti ir ļoti lieli. Piemēram, iedzīvotāju skaits Latvijā pārsniedz 2 miljonus. Statistiski novērot šādus lielus objektus ir grūti un tas maksā dārgi. Piemēram, līdzšinējo tautas skaitīšanu sagatavošanas darbi ilga vairākus gadus, un skaitīšanās piedalījās ap 5 tūkstoši cilvēku. Neskatoties uz to, tautas skaitīšanas programma ir jānoteic ļoti šaura - daži desmiti jautājumu. Ja gribētu par visiem iedzīvotājiem ievākt datus arī par viņu mājsaimniecības budžetu, tas būtu vienkārši nereāli.

            Dažu statistikas objektu pilnīga novērošana vispār nav iespējama. Piemēram, kontrolējot produkcijas kvalitāti, nevar noskaidrot visu elektrisko spuldžu lietošanas ilgumu, jo tas prasītu spuldzes iznīcināt pārbaudes procesā.

            Tādēļ statistika cenšas izstrādāt zinātniski pamatotus paņēmienus, ar kuru palīdzību, novērojot tikai zināmu daļu interesējošā objekta vienību, var pietiekoši pamatoti spriest par visa objekta raksturīgām īpašībām.

            Par ģenerālkopu sauc visu statistiskās izziņas objektu, to vienību kopumu, par kuru vēlas iegūt statistisku informāciju. Ģenerālkopa var būt galīga un eksistēt reāli. Tad principā, to var novērot pilnīgi, bet bieži tas nav lietdderīgi praktisku apsvērumu dēļ. Pilnīga novērošana pēc samērā plašas programmas ir nepieņemami darbietilpīga un dārga. Galīgas, reāli eksistējošas ģenerālkopas piemērs - visi Latvijas iedzīvotāji. Par neierobežotu ģenerālkopu jeb hipotētisko kopu sauc tādu statistikas objektu, kurš, atšķirībā no galīgas ģenerālkopas, nav ierobežots. Hipotētisko kopu pēc vēlēšanās var neirobežoti paplašināt. Piemērs - elektriskās spuldzes, ko ražo rūpniecība. Hipotētiskās kopas veido visi speciāli organizēti eksperimenti, jo teorētiski tos var atkārtot neierobežoti daudz reižu.

            Ar hipotētiskās kopas jēdzienu jāsaskaras vienmēr, ja grib izmantot statistikas datus prognozēšanā. Tagadnē principā nevar novērot tos notikumus un parādības, kuras notiks tikai nākotnē. Tādēļ šādas hipotētiskas kopas pilnīga novērošana ir neiespējama ne vien praktiski, bet arī teorētiski.

            Par nepilno statistisko novērošanu sauc novērošanu, kuras rezultātā ievāc datus nevis par visām, bet tikai par daļu no interesējošās ģenerālās vai hipotētiskās kopas vienībām. Nepilnas novērošanas paveidi ir daļēja novērošana un izlases novērošana.

            Par daļēju novērošanu sauc datu savākšanu par kādu ģenerālkopas daļu ar nolūku iegūt tikai vispārēju priekšstatu par statistikas objektu. Novērojamo vienību izvēle (atlase) notiek ekspertīzes ceļā, līdz ar to arī tikai ekspertīzes ceļā var spriest, kā novērotās parādības pārstāv (reprezentē) ģenerālkopu. Daļējā novērošana zinātniski maz pamatota, un statistikas praksē to lieto reti.

            Izlases novērošanas mērķis ir iegūt objektīvu, zinātniski pamatotu informāciju par visu ģenerālkopu (statistikas pētījuma objektu), no kura ir ņemta izlase.

            Tātad par izlasi jeb izlases kopu sauc to ģenerālās vai hipotētiskās kopas daļu, kuru praktiski novēro, lai spriestu par visas ģenerālās vai hipotētiskās kopas īpašībām.

            Turpmāk, runājot par ģenerālo un hipotētisko kopu, vienkāršības dēļ teiksim tikai "ģenerālkopa", ja vien nebūs vajadzības uzsvērt šo jēdzienu atšķirību.

            Par izlases metodi sauc zinātniski pamatotas statistikas metodes, ar kuru palīdzību:

            1) izveido izlasi, resp., atlasa novērojamās vienības no visām ģenerālkopas vienībām;

            2) organizē izlases novērošanas procesu un veic specifisku, tikai ar izlasi saistītu datu apstrādi, iegūtos secinājumus vispārina uz ģenerālkopu;

            3) aprēķina izlases reprezentācijas kļūdas, vērtējuma intervālus un novērtē iegūtos rezultātus kopumā.

            Ar izlases metodi, ja to veic atbilstoši statistikas zinātnes prasībām, var iegūt objektīvus, pareizus un reprezentatīvus ģenerālkopas īpašību vērtējumus. Tomēr šie vērtējumi nevar būt pilnīgi precīzi, jo izlase ar ģenerālkopu nav identiska. Tādēļ identiski nevar būt to raksturotāji. Strādājot ar izlasi, ir jārēķinās ar visiem kļūdu veidiem, kādus aplūko statistikas teorijā (novērošanas, reģistrācijas, sakopošanas). Pret šīm kļūdām ir jācīnās un tās jānovērš, veicot savākto datu pilnības, aritmētisko, loģisko un citas pārbaudes. Bez tam, strādājot ar izlasi, klāt nāk reprezentācijas kļūdas.

            Par reprezentācijas kļūdu jeb vienkārši izlases kļūdu sauc zināmu izlases un ģenerālkopas raksturotāju neatbilstību, jo šīs kopas nav identiskas. Izlases kļūda ir saistīta ar izlases metodes būtību, un principā to novērst nevar.

            Reprezentācijas kļūda piemīt arī daļējai novērošanai. Daļējās novērošanas gadījumā nevar novērtēt reprezentācijas kļūdas lielumu. Izlases metodes īpatnība un priekšrocība ir tā, ka ir iespējams objektīvi pareizi novērtēt reprezentācijas (izlases) kļūdas lielumu. Pat vairāk: izlases metodes pareiza izmantošana ļauj regulēt izlases kļūdas lielumu, to var samazināt līdz noteiktam, katrā gadījumā pieļaujamam lielumam, kā arī ar iepriekš izraudzītu drošību (varbūtību) garantēt pieļaujamās kļūdas robežu, par kuru lielāka tā nevar būt.

            Izlases metode ir cieši saistīta ar varbūtību teoriju un tieši uz to balstās. Varbūtību teorijas zināšanas ir nepieciešamas, novērtējot izlases kļūdas.

            Tātad, izlases novērošanas trūkums, salīdzinot ar pilno novērošanu, ir izlases kļūda. Toties izlases novērošanai ir virkne priekšrocību:

            1) ir iespējams iegūt informāciju par hipotētiskām kopām, kuras pilnībā novērot nav iespējams;

            2) sakarā ar mazāku novērojamās kopas lielumu var ātrāk veikt novērošanu, apstrādāt savāktos datus, ja pētījuma rezultāti ir vajadzīgi operatīvu lēmumu pieņemšanai;

            3) būtiski samazinās ar statistikas darbu saistītie izdevumi, ir iegūstams liels ekonomisks efekts;

            4) sakarā ar mazāku darba apjomu iespējams to rūpīgāk vadīt un kontrolēt, izmantot kvalificētākus darbiniekus, samazināt dažādas reģistrācijas un sakopošanas kļūdas, ir iespējams datus rūpīgāk pārbaudīt;

            5) ir iespējams paplašināt novērošanas programmu. Lai ievērotu reālās laika un finansiālas iespējas, jo plašāka un sarežģītāka ir novērošanas programma, jo mazākai jābūt novērojamai kopai. To pašu var formulēt pretēji: jo lielāku kopu vēlas novērot, jo šaurākai jābūt novērošanas programmai.

            Ir pat norādījumi, ka izlases rādītāju kopējā kļūda dažos gadījumos var būt mazāka nekā visas ģenerālkopas novērojumu rezultātā iegūto rādītāju kļūda. Tāds stāvoklis var rasties tad, ja, reģistrācijas, datu apstrādes u.c. kļūdas izdodas samazināt tiktāl, ka šis ieguvums ir lielāks par reprezentācijas kļūdu, kura vienmēr ir izlases metodes neizbēgams zaudējums.

            Ņemot vērā izlases metodes priekšrocības, rietumvalstu statistikas praksē tā lielā mērā aizstāj pilno novērošanu visās statistikas nozarēs. Dažādi pētījumi bioloģijā, tehnikā, lauksaimniecībā utt., visi pētījumi, kas saistīti ar iedzīvotāju dzīves līmeņa problēmām, preču pieprasījuma studēšanu izmanto izlases metodi.

            Kā ģenerālkopu, tā no šīs kopas ņemtu izlasi var raksturot ar dažādiem statistiskiem rādītājiem. Piemēram, vienai un otrai var aprēķināt interesējošās pazīmes aritmētisko vidējo, citas pazīmes relatīvo biežumu, modu, mediānu, dispersiju, variācijas koeficientu utt.

            Rādītājus, kuri aprēķināti pēc ģenerālkopas datiem, statistikā sauc par parametriem un apzīmē, kur tas iespējams, ar grieķu burtiem. Ja ģenerālkopu nenovēro, tās parametri nav zināmi. Tādā gadījumā viņus tāpat apzīmē ar grieķu burtiem, uzlūkojot par nezināmiem lielumiem. To tuvinātas nozīmes, precīzāk - intervālus, kuros parametri varētu atrasties, novērtē pēc izlases datiem.

            Atbilstošos rādītājus, kuri aprēķināti pēc izlases datiem (aritmētisko vidējo, relatīvo biežumu, standartnovirzi u.c.) sauc par izlases raksturotājiem, vērtējumiem, statistikiem¹.

____________________

¹  Diezgan burtisks aizguvums no angļu "statistic" arī krievu "статистик".

   Latviešu valodā šis svešvārds - statistiki - pagaidām maz ieviesies, jo tas fonētiski ir gandrīz homonīms vārdam ar citu nozīmi - statistikas darbinieks.

            Vērtējumus, kas aprēķināti pēc izlases datiem, apzīmē ar latīņu (latviešu) burtiem, cenšoties, ja vien iespējams, izvēlēties atbilstošus burtus tiem grieķu burtiem, ar kuriem apzīmē analogus parametrus.

            Dažu svarīgāo parametru un to vērtējumu simboli ir šādi:

 

Nosaukums	Parametrs	Vērtējums jeb statistiks
Aritmētiskais vidējais	m (mī), mx, my, F(x), m(y)	_   _   _ x; y; z; ...
Dispersija	s² (sigma)	s²
Vidējā kvadrātiskā novirze   (standartnovirze)	s	s
Korelācijas koeficients	r (ro)	r; R
Vienību skaits	N	n
Varbūtība un relatīvais biežums	R	v, w
Vispārīgs rādītājs (jebkurš)	q (teta)	T

 

            Vispārēju ģenerālkopas parametru apzīmē ar grieķu burtu teta q, atbilstošo vērtējumu, kas aprēķināts no izlases datiem, ar T. Šo lielumu starpības absolūtā vērtība ir reprezentācijas absolūtā kļūda. To apzīmē ar grieķu e (mazais epsilon):

Tātad

e = êq - T÷ .

 

            Pilnīga konsekvence un standartizācija apzīmējumos vēl nav panākta.

            Izlases kļūdas var būt sistemātiskas un nejaušas.

            Par sistemātiskām sauc tādas izlases kļūdas, kas rodas nepareizas vai pārlieku vienkāršotas izlases organizēšanas rezultātā. Lai nepieļautu sistemātiskas izlases kļūdas, galvenokārt ir jānodrošina visām ģenerālkopas vienībām vienāda iespēja iekļūt izlasē. Tas ir jāpanāk, rūpīgi organizējot izlasi.

            Nejaušo gadījuma izlases kļūdu rašanās ir saistīta ar pašu izlases metodes būtību, jo neviendabīgas kopas daļa nevar precīzi atbilst visai kopai. Tāpēc šīs kļūdas nevar pilnīgi novērst, lai cik rūpīgi organizē izlasi. Toties tās, atbilstoši vispārējam nejaušu kļūdu likumam, lielā mērā savstarpēji dzēšas. Ir iespējams aprēķināt nejaušo izlases kļūdu varbūtējos lielumus. Bez tam, attiecīgi organizējot izlasi, var samazināt kļūdu līdz tādam lielumam, kas ir konkrētā gadījumā pieļaujams.

            Tātad var secināt, ka sistemātiskās izlases kļūdas rodas no izlases metodes prasību neievērošanas. Tās principā var novērst. Lai to izdarītu, nedrīkst pieļaut nekādas atkāpes darba vienkāršošanai, paviršības un nolaides atlases procesā. Nejaušās izlases kļūdas galvenokārt ir atkarīgas no izlases lieluma, veida un pētāmās pazīmes variācijas.

            Sistemātisko izlases kļūdu var novērst, ja nodrošina visām ģenerālkopas vienībām pilnīgi vienādu iespēju nokļūt izlasē. To panākt ir diezgan grūti. Vislabākos rezultātus dod vienkārša gadījumizlase jeb īsti nejaušā izlase, kad izlasē iekļaujamās ģenerālkopas vienības izraugas ar kādas izlozēm raksturīgas procedūras palīdzību. Izloze jāorganizē ļoti rūpīgi, novēršot jebkādu apzinātu vai neapzinātu darbību tās rezultātu ietekmēšanai.

            Nejaušās izlases kļūdas ir atkarīgas no diviem faktoriem:

            1) no izlases lieluma (vienību skaita izlasē);

            2) no pētījamās pazīmes variācijas ģenerālkopā.

            Pirmā faktora ietekme uz izlases kļūdu ir apgriezta: jo lielāka izlase, jo mazāka izlases kļūda un otrādi.

            Otra faktora ietekme ir tieša: jo lielāka ir pazīmes variācija, jo lielāka ir izlases kļūda un otrādi: jo līdzīgākas pēc pētāmās pazīmes ir ģenerālkopas vienības, jo mazāka izlases kļūda.

            Nejaušo reprezentācijas kļūdu var samazināt divejādi

            - palielinot novērojamo vienību skaitu izlasē:

            - izvēloties racionālu (optimālu) izlases izveidošanas paņēmienu (atlasi) un ievērojot citas ar šo metodi saistītas prasības.

            Pirmās iespējas izmantošana ir ierobežota, jo, ejot šo ceļu, pakāpeniski zūd izlases metodes priekšrocības. Tādēļ, cik vien iespējams, ir jāizmanto iespējas, ko dod izlases pareiza un zinātniska organizācija, jo tas nav saistīts ar lielu papildus darba un līdzekļu patēriņu. Galvenais šeit ir statistiķa teorētiskās zināšanas, praktiskā pieredze un apzinīgs darbs.

 

5.2. Izlašu veidi

 

            Katram izlases veidam ir specifiska novērojamo vienību atlases metodika un tehnika. Izlases veidus klasificē pēc tā, ar kādiem paņēmieniem izlasi izdala no ģenerālkopas.

             Vadoties pēc novērojamo vienību atlases tehnikas, izšķir gadījumizlasi jeb izlasi ar izlozi un mehānisko izlasi.

            Izlase ar izlozi ir darbietilpīga, jo katrai ģenerālkopas vienībai ir jāsagatavo sava loze. Tādēļ tiešu lozēšanu aizstāj ar nejaušo skaitļu tabulām vai datora nejaušo skaitļu ģeneratoru. Ja ģenerālkopas vienības ir sanumurētas, tad vienības ar nejauši ģenerētiem numuriem iekļauj izlasē.

            Mehānisko izlasi izdara, sastādot ģenerālkopas vienību sarakstu, piemēram, alfabēta secībā un ņemot izlasē vienības, kas seko pēc noteiktiem intervāliem, piem., katru desmito, divdesmito u.tml. Saraksta vietā var izmantot reģistru datorā. Rindu, no kuras izdara atlasi, var saprast kā eksistējošu laika plūsmā, piem., aptaujājot katru 50. pircēju, kas ienāk veikalā u. tml.

            Atlase var būt individuāla, ja izlases (novērošanas) vienības atlasa katru atsevišķi vai grupveida, ja atlasa uzreiz veselas grupas (sērijas, ligzdas). Grupveida atlasē jāatšķir atlases vienība un novērošanas vienība, kas parasti ir arī kopas vienība. Atlases vienība šajā gadījumā ir vesela novērošanas vienību grupa. Līdz ar to atlases vienību skaits grupveida atlasē ir daudz mazāks par novērošanas vienību skaitu.

            Izlase var būt atkārtota vai neatkārtota. Atkārtotas izlases gadījumā vienreiz atlasīta vienība no tālākas atlases neizstājas un principā to var atlasīt arī otro, trešo utt. reizes. Neatkārtotas izlases gadījumā vienreiz atlasīta vienība turpmākās atlases procesā, piem., izlozē vairāk nepiedalās.

            Izlasi var izdarīt vai nu tieši no visas ģenerālkopas, to iepriekš nesadalot daļās, vai arī iepriekš sagrupējot raksturīgās grupās. Pirmajā gadījumā ir runa par vienpakāpes izlasi. Otrajā gadījumā var būt divi varianti. Ja atlasi izdara no visām ģenerālkopas grupām, tad arī iegūst vienpakāpes izlasi, bet no grupēta (stratificēta) vai citādi sakārtota statistiskā objekta. Ja vispirms atlasa daļu no grupām, bet pēc tam atlasīto grupu ietvaros atsevišķas vienības, iegūst divu, bet vispārējā gadījumā daudzpakāpju izlasi.

            Praktiski organizējot izlasi, minētos pamatpaņēmienus bieži savstarpēji kombinē. Atlases paņēmiena izvēle parasti ir atkarīga no statistikas objekta īpatnībām, ģenerālkopas lieluma (ļoti lielām ģenerālkopām un it sevišķi hipotētiskai kopai pilnu vienību saraksu nevar sastādīt), kā arī no darbam atvēlētā laika un līdzekļiem. Dažos gadījumos statistiķiem ir zināma izvēles brīvība, kādu paņēmienu lietot.

            Praksē, ņemot vērā dažādas īpatnības, visbiežāk lieto šādus izlases veidus, kuri atšķiras galvenokārt ar atlases paņēmienu:

            1) vienkārša gadījumizlase jeb īsti nejaušā izlase;

            2) mehāniskā izlase;

            3) stratificētā jeb tipoloģiskā izlase;

            4) sērijveida jeb ligzdveida izlase;

            5) daudzpakāpju izlase;

            6) daudzfāzu izlase.

            Īpašs izlases veids ir t.s. mazās izlases, par kurām plašāk runā matemātiskās statistikas kursā.

5.2.1. Vienkārša gadījumizlase

 

            Vienkārša gadījumizlase jeb īsti nejaušā izlase vislabāk nodrošina visu kopas vienību vienādu iespēju nokļūt izlasē. Vienkāršā gadījumizlasē novērojamās vienības atlasa individuāli, izlozveidīgi un vienpakāpeniski no visas ģenerālkopas bez iepriekšējas grupēšanas. Lozēšanu parasti aizstāj ar nejaušo skaitļu tabulām vai nejaušo skaitļu ģeneratoru.

            Atlase var būt gan atkārtota, gan neatkārtota.

            Vienkārša gadījumizlase ir visu citu izlases veidu priekštece un teorētiski vispamatotākais izlases veids. Tomēr praksē to lieto reti, jo viņa ir darbietilpīga. Turklāt citi izlašu veidi, piemēram, stratificētā gadījumizlase, gandrīz ar to pašu darba patēriņu nodrošina mazāku izlases kļūdu.

            Vienkāršai gadījumizlasei visvieglāk aprēķināt izlases kļūdas. Tādēļ runājot par šīm kļūdām, vērtējuma intervāliem un citiem metodiskiem jautājumiem, īsti nejaušo izlasi aplūko kā pirmo.

            Ja statistisko objektu (ģenerālkopu) attēlo grafiski ar kādu figūru, tad ar vienkāršo gadījumizlasi atlasītās vienības (punkti) tajā izvietojas pilnīgi haotiski, skat. 5.1. attēla a zīmējumu.

 

 

c

b

a

	d		e

 

 

 

 

5.1 attēls. Dažādu izlašu veidu shematiska ilustrācija:

                                                a - vienkārša gadījumizlase,

                                                b - mehāniska izlase,

                                                c - stratificēta tipoloģiska gadījumizlase,

                                                d - sērijveida izlase,

                                                e - divpakāpju izlase.

 

 

 

 

 

 

 

5.2.2. Mehāniskā izlase

 

            Lai veidotu mehānisku izlasi, visas ģenerālkopas vienības sakārto pēc kādas formālas pazīmes. Tā var atspoguļot kopas vienību izvietojumu teritorijā, to rašanās secību laikā vai kādu citu formālu pazīmi, piem., izmantojot sakārtojumu pēc alfabēta. Izlasē ņem tās vienības, kuras secīgi atrodas noteiktā attālumā no iepriekšējās vienības. Izlases attālumu jeb soli nosaka izlases vienību skaita attiecība pret ģenerālkopas vienību skaitu. Ja grib iegūt 10% izlasi, ņem katru desmito vienību, ja grib iegūt 5% izlasi - katru divdesmito utt. Pirmo vienību vēlams ņemt pimā soļa centrā.

            Shematiskā attēlā mehāniski atlasītās vienības izkārtojas, veidojot kādu ornamentu, skat. 5.1. att. b zīmējumu.

            Ja ģenerālkopā vienības sakārtotas pēc kādas formālas pazīmes, piem., alfabēta, mehāniskās izlases reprezentativitāte atbilst vienkāršas gadījumizlases reprezentativitātei. Tādēļ mehāniskās izlases rezultātus novērtē, izmantojot vienkāršās gadījumizlases kļūdu formulas.

            Mehānisko izlasi no ranžētas rindas iegūst, ja kopas vienības ir sakārtotas kādas būtiskas pazīmes augošā vai dilstošā secībā; pēc pazīmes, kuru pašu pētī vai tā ir cieši saistīta ar pētījamo pazīmi. Šādas izlases reprezentivitāte ir augstāka. Tā ir tuva stratificētas izlases reprezentativitātei, tikai izlases kļūdas grūti aprēķināt.

            Tā kā parasti vienlaikus novēro nevis vienu, bet daudz pazīmes, no ranžētas rindas ņemtas mehāniskās izlases priekšrocības grūti novērtēt. Tādēļ arī šajā gadījumā parasti izlases kļūdas novērtē ar vienkāršai gadījumizlasei domātajām metodēm, ņemot vērā, ka īstajiem rezultātiem vajadzētu būt labākiem.

            Mehānisko izlasi plaši lieto, ja atlase jāizdara no neierobežotas (hipotētiskās) ģenerālkopas. Šajā gadījumā visu vienību sarakstu sastādīt nevar un līdz ar to vienību izloze nav iespējama. Piemēram, pētījot neapmierināto pieprasījumu, var aptaujāt katru desmito (divdesmito vai piecdesmito) pircēju, kurš iznāk no veikala. Tādā pat veidā var veikt produkcijas kvalitātes pētījumus, ņemot pārbaudei izstrādājumus no konveijera lentas utt.

 

5.2.3. Stratificēta jeb tipoloģiskā gadījumizlase

 

            Veicot šādu izlasi, visu ģenerālkopu sadala tipiskās, iekšēji pēc iespējas vienveidīgās, bet savstarpēji atšķirīgās grupās jeb stratās. Pēc tam vienību atlasi veic katras grupas ietvaros atsevišķi, parasti izmantojot vienkāršas gadījumizlases vai mehāniskās izlases paņēmienu.

            Shematiskā attēlā atlasītās vienības izvietojas vai nu haotiski vai veidojot ornamentu katra laukuma (grupas) ietvaros, skat. 5.1. attēla c zīmējumu.

            Stratificēta izlase un tās modifikācijas ir ļoti izplatītas statistikas praksē.

            Strādājot ar šo izlases veidu, vienkāršākā ir proporcionālā izlase, kad no katras grupas ņem vienību skaitu, kurš ir proporionāls šīs grupas lielumam.

            Proporcionālas, stratificētas izlases reprezentācijas kļūda ir atkarīga no tā, kā pētījamās pazīmes dispersija sadalās intragrupu (iekšgrupu) un intergrupu (starpgrupu) dispersijā.

            Ja grupēšanu izdara pēc pētījamās vai ar to cieši saistītas pazīmes, tad stratificēta izlase maksimāli pilnīgi reprezentē visas ģenerālkopas grupas. Tādēļ ka variācijas daļa, kas atspoguļojas starpgrupu dispersijā, reprezentācijas kļūdu nerada.

            Turpretī intragrupu dispersiju izraisa statistiķim nezināmi, var teikt nejauši cēloņi. Tādēļ intragrupu variācija nosaka stratificētās izlases kļūdu, resp., tās reprezentativitāti.

            Tā kā intragrupu (iekšgrupu) dispersija vienmēr ir mazāka par kopējo (parasto) dispersiju, ja arī atsevišķos gadījumos dažādā mērā, tad stratificētā izlase pie citiem līdzīgiem nosacījumiem vienmēr ir reprezentatīvāka par vienkāršu gadījumizlasi. Tādēļ arī viņa ir plaši izplatīta praksē.

            Bez proporcionālās tipoloģiskās izlases ir zināmi citi tipoloģiskās izlases veidi.

 

 

5.2.4. Sērijveida izlase

 

            Sērijveida (sēriju jeb ligzdveida) izlasi bieži lieto tad, ja ģenerālkopa dabiski dalās novērojamo vienību apakškopās. Piemēram, izstrādājumi, kuri iepakoti kastēs, iedzīvotāji, kas dzīvo vienā namā vai saimniecībā utt. Šādos, kā arī dažos citos gadījumos praktiski nav izdevīgi atlasīt katru novērojamo vienību atsevišķi. Vieglāk ir atlasīt veselas grupas jeb sērijas (saimniecības, kastes utt.) un novērot visas vienības, kas ietilpst atlasītajā sērijā. Sēriju atlasi var veikt ar vienkāršas gadījumizlases atkārtoto vai neatkārtoto paveidu vai citādi. Katru atlasīto sēriju novēro pilnīgi, resp., savāc datus par visām tās vienībām.

            Shematiskajā attēlā atlasītās vienības blīvi aizņem savas sērijas. Ārpus šīm sērijām izlasē nokļuvušu vienību nav, skat. 5.1. attēla d zīmējumu.

            Tā kā visas atlasītās sērijas novēro pilnīgi, pazīmes variācija atlasīto sēriju ietvaros reprezentācijas kļūdu nerada. Reprezentācijas kļūdu rada vienīgi starpsēriju variācija, ko mērī ar starpsēriju dispersiju. Ir lietderīgi ievērot, ka stratificētās izlases gadījumā bija tieši otrādi.

            No dispersiju saskaitīšanas teorēmas viedokļa sēriju izlase būtu reprezentatīvāka par vienkāršo gadījumizlasi. Bet tajā pašā laikā praktiski nevar novērot tik daudz sēriju r kā atsevišķi ņemtu kopas vienību n. Tādēļ r << n, līdz ar to sēriju izlase vienmēr ir mazāk reprezentatīva nekā īsti nejaušā izlase.

 

5.2.5. Daudzpakāpju izlase

 

            Vienpakāpes izlasēs izlases vienību atlasi veic, izmantojot vienu izlases pamatu. Par atlasi neskaita tipoloģisko grupu jeb stratu izdalīšanu, tāpat visu vienību novērošanu atlasītajās sērijās, jo nekāda atlase šeit nenotiek.

            Organizējot daudzpakāpju izlasi, izlases kopu veido pakāpeniski. Vispirms pirmajā pakāpē no ģenerālkopas atlasa lielāka apjoma sērijas, no kurām otrajā pakāpē atlasa zināmu skaitu mazāka apjoma sēriju utt. Pēdējā atlases pakāpē atlasa tieši novērošanai paredzētās kopuma vienības.

            Daudzpakāpju izlase atvieglo un palētina izlases organizāciju. Tomēr tā rada lielāku reprezentācijas kļūdu nekā tāda pati apjoma vienpakāpes izlase.

            Izlases kļūda daudzpakāpju izlasē veidojas no visu izlases pakāpju kļūdām. Jo vairāk pakāpju izlasei, jo lielāka kopējā kļūda un jo grūtāk to aprēķināt.

            Samērā bieži lieto divpakāpju izlasi, kad pirmajā pakāpē atlasa sērijas, bet otrajā pakāpē - novērojamās kopas vienības.

            Shematiski izlases vienību izvietojumu ģenerālkopā divpakāpju izlasei var parādīt ar e zīmējumu 5.1. attēlā.

 

5.2.6. Daudzfāzu izlase

 

            Izlases metodes vispārējs princips nosaka, ka, jo plašāka un sarežģītāka ir novērošanas programma, jo mazākam ir jābūt novērošanas vienību skaitam izlasē un otrādi.

            Daudzfāzu izlase izmanto šo principu. Tajā novērojamo vienību skaits ir diferencēti saistīts ar novērošanas programmas plašumu un sarežģītību.

            Piemēram, organizējot tautas skaitīšanu, var rīkoties šādi:

            1) pašas svarīgākās ziņas (dzimums, vecums, tautība u.c.) savākt par visiem iedzīvotājiem, te izlases pagaidām nav;

            2) par 20% iedzīvotāju savākt ziņas arī par viņu darba vietu, nodarbošanos, dzīvokli u.c. (20% izlase), tā būs izlases viena fāze;

            3) par 1% iedzīvotāju savākt dažas ziņas par ģimenes budžetu (1% izlase), tā būs izlases otra fāze.

            Daudzfāzu izlasē katra fāze būtībā ir patstāvīga izlase. Vienīgi organizatoriski tās izveido un novēro vienlaikus. Atlases paņēmieni var būt dažādi. Visbiežāk izmanto mehānisko atlasi, katru nākošo fāzi izdalot no iepriekšējās.

            Daudzfāzu izlases kļūda katrai fāzei ir atšķirīga. Tādēļ tās aprēķina katrai fāzei atsevišķi. Aprēķiniem nav īpašu formulu. Jāizmanto tās formulas, kuras atbilst tam izlases veidam, ar kuru atlasīta interesējošā fāze.

Pēdējā laikā teorētiski vienkāršākos izlases pamatveidus dažādi kombinē.

 

5.3. Ģenerālkopas vērtējumu aprēķināšana

 

            Katras izlases īstais mērķis ir iegūt statistisku informāciju nevien par reāli novēroto izlasi, bet arī un galvenokārt par ģenerālkopu, no kuras izlase ņemta un kuru izlase pārstāv.

            Tādēļ nākošais solis pēc izlases datu apstrādāšanas ir to attiecināšana uz ģenerālkopu. Šo procesu sauc arī par datu izplatīšanu uz ģenerālkopu, izlases paplašināšanu u.c.

            Ģenerālkopas rādītāju vērtējumu aprēķināšanas tehnika ir atkarīga no izdarītās izlases veida un no tā, kādi rādītāji tiek "izplatīti": absolūtie, relatīvie, vidējie u.c. Dažos gadījumos šis darbs ir ļoti vienkāršs, citos - pietiekami sarežģīts.

 

5.3.1. Vienkārša gadījumizlase

 

            Par vienkāršo gadījumizlasi jeb īsti nejaušo izlasi, kā to parādījām iepriekš, sauc izlasi, ja izlasē iekļaujamās ģenerālkopas vienības atlasa vienā pakāpē ar kādu izlozei raksturīgu procedūru. Līdzvērtīga ir arī vienpakāpes mehāniskā izlase.

            Ģenerālkopas vērtējumu aprēķināšana pēc vienkāršas gadījumizlases rezultātiem ir tehniski visvienkāršākā.

 

            5.1. uzdevums. No ģenerālkopas, kas sastāv no 100 vienībām, vienkāršas gadījumizlases ceļā ir izraudzītas un novērotas 10 vienības, iegūstot 5.1.tabulas 1.,2. ailēs parādītos datus. Aprēķināt parādības apjoma (absolūtā lieluma, datu summas) vērtējumu ģenerālkopā, šīs pazīmes aritmētisko vidējo un variācijas rādītājus.

            Tiklab ģenerālkopas kā arī izlases vienību skaits ir ņemts statistikas praksei neraksturīgi mazs, lai aprēķinus varētu sakārtot nelielā, pārskatāmā tabulā.

 

5.1. tabula

1.uzdevuma dati un aprēķiniem izmantotie starprezultāti

 

Nr.  i
1	5	0,1	50	10	0	0	250
2	2	0,1	20	10	-3	9	40
3	7	0,1	70	10	2	4	490
4	3	0,1	30	10	-2	4	90
5	4	0,1	40	10	-1	1	160
6	5	0,1	50	10	0	0	250
7	8	0,1	80	10	3	9	640
8	1	0,1	10	10	-4	16	10
9	9	0,1	90	10	4	16	810
10	6	0,1	60	10	1	1	360
S	50	1,0	500	100	0	60	3100

            Uzdevuma analīze un atrisinājums. Tā kā izlase izveidota kā vienkārša gadījumizlase, ģenerālkopas vērtējumus var iegūt ļoti vienkārši. Šādu atrisinājuma gaitu nosauksim par speciālpaņēmienu. To pašu rezultātu var iegūt, lietojot universālpaņēmienu, kas konkrētajā gadījumā šķiet sarežģītāks, bet ir izdevīgs tad, ja ir izmantots cits izlases veids. Tādēļ arī ar šo paņēmienu jāiepazīstas vienkāršākā izlases veida ietvaros.

            Speciālpaņēmiens vienkāršai gadījumizlasei.

            a. Datu summa jeb parādības apjoms izlasē (absolūtais lielums), kā tas redzams 5.1. tabulas 2.ailes pēdējā rindā ir Sx=50. Lai atrastu datu summas vērtējumu ģenerālkopā, šī summa jāpareizina ar skaitli, kas rāda, cik reizes ģenerālkopas vienību skaits N ir lielāks par izlases vienību skaitu n:

 

                                                                                        (5.1.)

resp.

            b. Izlases vidējo pieņem par labāko zināmo ģenerālkopas vērtējumu tiešā veidā. Par izlases kļūdu un vērtējumu intervālu noteikšanu runāsim nākošā nodaļā. Tātad ģenerālkopas vidējais m ir:

                                                                                                 (5.2)

resp.

 

            Ja vidējo aprēķina no absolūtajiem lielumiem, statistisko svaru lietošana nav vajadzīga.

            c. Arī izlases dispersiju s² var uzlūkot par ģenerālkopas dispersijas s² labāko pieejamo vērtējumu. Lai panāktu vienkāršāku salīdzinājumu ar turpmāk parādīto universālo paņēmienu, korekciju ar brīvības pakāpju skaita zudumu neizdarīsim.

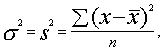                                                                               (5.3.)

(izdarot korekciju ar brīvības pakāpju skaita zudumu, saucējā jāņem n-1),

Uzdevumā (skat. 5.1. tabulu):

            Plašākiem praktiskiem aprēķiniem ērtāka ir momentu metodes formula:

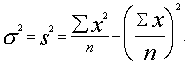                                                                         (5.4)

            Standartnovirze:

                                                                                                 (5.5)

Uzdevumā:

bet variāciju koeficients

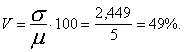
            Universālpaņēmiens paredz katrai izlases kopas vienībai piekārtot varbūtību, ar kādu tā nonākusi izlasē P_i, kur i - vienības numurs. Vienkāršas gadījumizlases gadījumā visu vienību varbūtības ir vienādas, t.i. P₁= P₂=...=P_n, un šīs metodes lietošana šķiet nepamatoti sarežģīta. Viņa kļūst lietderīga un efektīva, lietojot kādas sarežģītākas atlases shēmas, kur varbūtība nonākt izlasē katrai izlases vienībai (vai to grupām) ir atšķirīga.

            a. Datu summu (absolūto lielumu) ģenerālkopā aprēķina,  katru izlases novērojumu dalot ar tā varbūtību un dalījumus summējot.

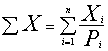.                                                                                            (5.6)

            Vienkāršā gadījumizlasē svaru sitēma P_i ir veidota tā, lai svaru summa visā izlasē būtu viens:

   (i = 1, 2, ..., n) ; SP_i=1.

            Uzdevuma atrisinājums ir izskaitļots 5.1.tabulas 4.ailē: Sx=500, kas sakrīt ar iepriekšējo.

            Reālās izlasēs varbūtības P_i bieži ir ļoti mazi skaitļi. Lai aprēķini būtu saprotamāki, dažkārt dalīšanu ar varbūtībām aizstāj ar reizināšanu ar varbūtībām apgrieztiem skaitļiem. Tos sauc par izlases vienību statistiskajiem svariem. Šāds “svars” parāda, cik ģenerālkopas vienību pārstāv katra izlases vienība.

            b. Iestrādājot varbūtības aritmētiskā vidējā formulā, iegūstam:

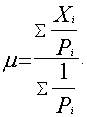                                                                                                  (5.7)

            Ja visas varbūtības P_i ir vienādas, ģenerālkopas vidējais m ir vienāds ar izlases vidējo . Uzdevumā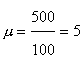 (izmantotas 5.1. tabulas 4. un 5. ailes summas). Ja varbūtības ir dažādas, ģenerālkopas vidējais un izlases vidējais atšķiras.

            c. Iestrādājot varbūtības dispersijas momentu metodes formulā, iegūstam

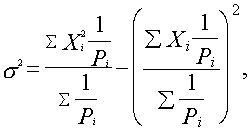                                                          (5.8)

            Uzdevumā

(dati ievietoti no 5.1. tabulas kopsummu rindas).

            Arī šī formula vienkāršas gadījumizlases gadījumā dod identiskus rezultātus parastai formulai, jo visi P_i ir vienādi. Ja P_i ir dažādi, ģenerālkopas dipersija un izlases dispersija atšķiras.

 

5.3.2. Stratificēta gadījumizlase

 

            Stratificētu gadījumizlasi jeb tipoloģisku izlasi iegūst tad, ja visu ģenerālkopu sadala grupās, strātās jeb tipos un no katras šādas strātas ņem vienkāršu gadījumizlasi.

            Šāda izlase ir pieskaitāma vienpakāpes izlasēm, jo izlase notiek tikai strātu ietvaros. Izlasē iekļaujamās strātas neizvēlas, bet izlasē ņem visas strātas. Tādēļ šeit nekāda izlase nenotiek.

            Strātas var veidot tiklab pēc teritoriālas pazīmes (rajoni, pilsētas, pagasti), kā arī pēc kādas sociālekonomiskam pētījumam būtiskas kvantitatīvas vai atributīvas pazīmes.

            Latvijas Centrālā statistikas pārvalde, izdarot iedzīvotāju lauksaimniecības uzņēmumu izlaseveida aptauju 1995.g. patstāvīgu atlasi veica no šādām saimniecību grupām, grupējot tās pēc rīcībā esošās platības:

                        virs 20 ha,

                        no 1,0 līdz 20,0 ha,

                        no 0,1 līdz 1,0 ha,

                        mazākas par 0,1 ha²

            Izlases izvietojums starp pirmajām trim iedzīvotāju saimniecību grupām tika noteikts proporcionāli attiecīgās grupas iedzīvotāju saimniecību rīcībā esošai kopējai zemes platībai.

            Sekojošais uzdevums stipri vienkāršotā veidā imitē minēto izlasi.

 

            5.2.uzdevums. Kādā teritorijā, piemēram, pagastā ir 50 individālās lauku saimniecības, kuru rīcībā ir šādas zemes platības (5.2. tabula).

Aprēķināt visas ģenerālkopas statistiskos parametrus, pēc tam ģenerālkopu sadalīt trīs strātās (0,1 - 1,0; 1,0 - 20; virs 20), no katras strātas ņemt kopējai zemes platībai proporcionālu izlasi, tā, lai kopējais vienību skaits izlasē būtu 10.

            Aprēķināt izlases raksturotājus un salīdzināt tos ar ģenerālkopas parametriem.

 

5.2. tabula

Ģenerālkopas saimniecību zemes platība.

 

1. strāta		2. strāta		3. strāta
Kārtas Nr. i	Platība xi	Kārtas Nr. i	Platība xi	Kārtas Nr. i	Platība xi
1	0,1	21	1	41	30
2	0,1	22	2	42	40
3	0,2	23	3	43	50
4	0,2	24	4	44	60
5	0,3	25	5	45	70
6	0,3	26	6	46	80
7	0,4	27	7	47	90
8	0,4	28	8	48	100
9	0,5	29	9	49	120
10	0,5	30	10	50	140
11	0,6	31	11
12	0,6	32	12
13	0,7	33	13
14	0,7	34	14
15	0,8	35	15
16	0,8	36	16
17	0,9	37	17
18	0,9	38	18
19	1,0	39	19
20	1,0	40	20
S	11,0	S	210	S	780
				SS	1001

 

 

 

 

___________

² Pielikums statistikas biļetenam “Lauku saimniecības Latvijā 1995.g.” - 1.-6. lpp.

            Analīze un atrisinājums. Uzdevums šķiet samākslots tādēļ, ka nav nozīmes vākt tādus datus par izlasi, kādi jau ir zināmi par visu ģenerālkopu. Parasti par izlasi ievāc datus pēc daudz plašākas programmas (vairāki desmiti vai simti jautājumu), kamēr par visām ģenerālkopas vienībām ir zināmi dati tikai par dažām pazīmēm, nereti tikai vienību numuri kādā reģistrā.

            Tomēr nereti, izdarot izlasi, tās programmā ietver 1-3 jautājumus par pazīmēm, par kurām ir zināmi ģenerālkopas dati (uzdevumā - zemes platības). Tā rīkojas, lai varētu novērtēt izlases reprezentativitāti tiešu salīdzinājumu ceļā. To pazīmju izlases kļūdas resp., viņu reprezentativitāti, par kurām datus iegūst vienīgi izlasē, var novērtēt, izmantojot matemātiskās statistikas metodes (nākošā apakšnodaļa).

            Apstrādāt visas ģenerālkopas datus var, izmantojot parastās variācijas rindas apstrādes formulas un kādu tipa programmu. Iegūstam:

           

                                      

 

                              

 

                                                           

 

(starpsummas 5.2. tabulas beidzamā rindā)

 

            Lai izveidotu 20% izlasi (n=10), kur atlasāmo vienību skaits ir proporcionāls pazīmei x, aprēķinam, cik vienību jāņem no katras grupas (strātas):

                       

                        1.grupa:  (vienības);

                        2.grupa:  (vienības);

                        3.grupa:  (vienības).

 

            Iznāk, ka no pirmās grupas izlasē nav jāņem neviena vienība, no otrās - divas vienības, no trešās - astoņas vienības (saimniecības).

            Taču, kā parādīsim paragrāfa beigās, ja kādu strātu atstāj bez pārstāvniecības izlasē, aplūkojamā metode dod neapmierinošus rezultātus. To ir pamanījuši arī Centrālās statistikas pārvaldes darbinieki un atzīmējuši iepriekš piezīmē minētā izdevumā.

            Tādēļ no 1.grupas ņemsim izlasē vienu vienību, no otrās - divas, no trešās - septiņas. Praktiskā darbā, kad veido daudz lielākas izlases, arī 1 - 2 vienības kādās no strātām jāuzlūko par nepietiekamu pārstāvniecību.

            Ņemot vērā no 5.2. tabulas saimniecībām iepriekšējām prasībām atbilstošu mehānisku izlasi no ranžētās rindas, kura ir reprezentatīvāka nekā vienkārša gadījumizlase, izlasē iekļaujam 10., 27., 34., 41., 42., 43., 45., 47., 49., 50. vienības.

            Varam aizpildīt darba tabulu (5.3. tabula)

 

 

 

 

 

 

 

5.3. tabula

Izlase, kur 1.grupā viens pārstāvis

 

i
10	0,5	0,05	20	10
27	7	0,1	10	70
34	14	0,1	10	140
41	30	0,7	1,4286	42,86
42	40	0,7	1,4286	57,14
43	50	0,7	1,4286	71,43
45	70	0,7	1,4286	100
47	90	0,7	1,4286	128,57
49	120	0,7	1,4286	171,43
50	140	0,7	1,4286	200
S	X	X	50	991,43

 

            x_i 5.3. tabulā ir zemes platība, atbilstoši 5.2. tabulas datiem. P_i - varbūtība i-tai saimniecībai nonākt izlasē. Piemēram, pirmajā strātā izlozējām vienu saimniecību, ar Nr. 10 no 20 saimniecībām, tādēļ P₁₀ = 1 / 20 = 0.05. Trešajā strātā ielozējam 7 saimniecības no 10. Tādēļ viņu varbūtības nonākt izlasē Pi = 7 / 10 = 0,7.

                  Varbūtību apgrieztie lielumi rāda, cik saimniecības ģenerālkopā pārstāv katra konkrēta izlasē nonākusī saimniecība. Piemēram, saimniecība Nr. 10 pārstāv 20 saimniecības, Nr 27. un 34. katra 10 saimniecības, bet pārējās izlasē nonākušās saimniecības - katra tikai 1,4286 ģenerālkopas vienības (saimniecības, 5.3.tabulas 4.aile).

            Lai ģenerālkopas vērtējumu aprēķināšanas formulas dotu pareizus rezultātus, jāpārliecinās, lai statistisko svaru apgriezto lielumu summa būtu vienāda ar ģenerālkopas vienību skaitu, uzdevumā N=50.

            Tā kā vienības izlasē iekļāvām ar ļoti atšķirīgām varbūtībām, tiešai izlases datu apstrādei nav jēgas un tās rezultāti var rupji izkropļot īstenību. Piemēram, formāli pēc 5.3. tabulas datiem Sx=561,5 un =56,2 (?) (ģenerālkopā m=20,0).

            Pētāmā absolūtā lieluma vērtējumu ģenerālkopā (visu 50 saimniecību kopējās zemes platības vērtējumu) pēc izlases datiem iegūstam ar formulu

 

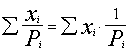                                                                                                                (5.9)

 

 (matemātiski identiskie pieraksti atšķiras ar interpretācijas iespējām).

            5.3. tabulā ir izskaitļots, k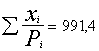a (ha).

Tas ir šajā gadījumā zināmā ģenerālkopas absolūtā lieluma 1001 ha vērtējums. Ņemot vērā mazo izlases vienību skaitu, atbilstība jāvērtē kā laba.

 

 

 

            Ar statistiskiskajiem svariem svērto izlases vidējo, kas būtībā ir ģenerālkopas vidējā vērtējums, atrod ar formulu

 

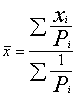                        .                                                                                                    (5.10)

 

Uzdevumā (ha).

 

            Dalījumu var interpretēt arī vienkārši kā kopējās platības vērtējuma dalījumu ar ģenerālkopas saimniecību skaitu.

            Vidējās saimniecības zemes platības vērtējums 19,8 ha ko ieguvām pēc izlases datiem, samērā precīzi sakrīt ar šajā gadījumā zināmo ģenerālkopas vidējo m=20,0 ha.

            Svērā izlases vidējā mazu izlases kļūdu konkrētajā uzdevumā nodrošina tas, ka vienkāršas gadījumizlases vietā ņēmām mehānisko izlasi no ranžētas rindas.

            Svērtā standartnovirze izlasē 33,79 arī maz atšķiras no standartnovirzes ģenerālkopā 33,12.

 

            Brīdinājums!

 

            Nākošajā 5.4. tabulā parādīsim, kādus rezultātus iegūstam, ja pirmo strātu (grupu) atstājam bez pārstāvja, bet trešajā strātā, atbilstoši aprēķiniem paragrāfa sākumā, ņemam 8 vienības (saimniecības).

            Citādi 5.4. tabula aizpildīta analogi 5.3. tabulai.

 

5.4. tabula

Izlase, kur 1.grupā nav pārstāvja

 

i
27	7	0,1	10	70
34	14	0,1	10	140
41	30	0,8	1,25	37,95
42	40	0,8	1,25	50
43	50	0,8	1,25	62,5
45	70	0,8	1,25	87,5
46	80	0.8	1,25	100
47	90	0,8	1,25	112,5
49	120	0,8	1,25	150
50	140	0,8	1,25	175
S	-	-	30	985

 

Pirmais brīdinājums, ka izlase nebūs reprezentatīva ir , kas neatbilst ģenerālkopas vienību skaitam 50.

 

Izrēķinot svērto izlases vidējo, iegūstam

 

  ha,

 

kas ir apmēram par 64 % lielāks nekā ģenerālkopas vidējais.

            Ja, strādājot ar apspriežamo metodi, kādu strātu atstājam bez pārstāvja, tad šādi izveidota izlase pārstāv citu ģenerālkopu - kura veidota tikai no tām strātām, kurām ir pārstāvji izlasē.

            Izrēķinot otrās un trešās grupas vidējo pēc ģenerālkopas 5.2. tabulas datiem, iegūstam

 

                       

 

kas labi atbilst jaunās izlases vidējam.

            No formālā viedokļa tādu rezultātu nodrošina varbūtībām apgriezto lielumu summa 30, kas sakrīt ar vienību skaitu ģenerālkopas otrajā un trešajā strātā.

 

5.3.3. Divpakāpju gadījumizlase

 

            Lai izdarītu divpakāpju gadījumizlasi, ģenerālkopu sadala grupās pēc kādas formālas pazīmes. Šīs grupas neveido kādus raksturīgus sociālekonomiskus v.c. tipus. Tādēļ atšķirības dēļ no iepriekšējā, tās nesauksim par strātām.

            Izlases pirmajā pakāpē, izmantojot gadījumizlasi, atlasa noteiktu skaitu grupu no lielāka grupu skaita ģenerālkopā.

            Izlases otrajā pakāpē izdara vienkāršu gadījumizlasi atlasītās grupas ietvaros.

 

            5.3. uzdevums. Izveidosim divpakāpju gadījumizlasi pēc 5.2. tabulas datiem tā, ka ģenerālkopas 50 saimniecības sadalām 10 grupās, lai visās būtu vienāds saimniecību skaits -5, bet saimniecību sadalījums pa grupām - nejaušs, neveidojot kādus kvalitatīvus vai kvantitatīvus tipus. Šim nolūkam saimniecības ierakstām 5.5. tabulas blokos, “izlozējot” viņu numuru, piemēram pēc gadījumskaitļu tabulām³ vai izmantojot gadījumskaitļu ģeneratoru.

            Praktiskā darbā grupas izveido pēc kādas formālas pazīmes, piemēram, pēc alfabēta, valsts reģistra numuriem v.c. Ja izmanto teritoriālu pazīmi, tā parasti veido tipiskas strātas. Tad jāizmanto stratificētas izlases metodes.

 

 

 

 

 

 

 

 

 

 

____________

³ Piemēram, Nf,kbws vfntvfnbxtcrjq cnfnbcnbrb. V.:DW FY CCCH> 1968. - c.428.-429.

5.5 tabula

 

Ģenerālkopas saimniecību zemes platība

 

1.grupa			2.grupa			3.grupa			4.grupa
i	xi		i	xi		i	xi		i	xi
10	0,5		11	0,6		23	3		19	1
37	17 °		9	0,5		4	0,2		33	13 °
8	0,4		44	60		35	15		18	0,9
12	0,6 °		15	0,8		45	70		48	100 °
31	11		25	5		32	12		22	2
5.grupa			6.grupa			7.grupa			8.grupa
i	xi		i	xi		i	xi		i	xi
42	40		27	7		47	90		5	0,3
1	0,1		50	140 °		29	9		20	1 °
6	0,3		21	1		24	4		49	120
26	6		40	20 °		16	0,8		14	0,7 °
41	30		39	19		28	8		30	10
9.grupa			10.grupa
i	xi		i	xi
17	0,9		2	0,1
7	0,4 °		36	16
46	80		43	50
3	0,2 °		13	0,7
34	14		38	18

           

            Lai šī uzdevuma rezultāti būtu salīdzināmi ar 5.2. uzdevumu, vienojamies izlasē iekļaut 10 vienības. To var izdarīt, piemēram, tā, ka izlases pirmajā pakāpē atlasām 5 grupas, bet otrajā pakāpē - 2 vienības katrā atlasītajā grupā. Atlase abās pakāpēs jāizdara ar kādu gadījumprocedūru, piemēram, izmantojot gadījumskaitļu tabulas vai ģeneratoru.

            Izrakstot no gadījumskaitļu tabulām pirmos piecus skaitļus, kas mazāki vai vienādi ar 10, iegūstam: 9; 8; 4; 6; 1. Grupas ar šiem numuriem jāņem izlasē (ja gadījumskaitļu tabulā kāds skaitlis atkārtojas, jāņem nākošais).

            Izlases otrai pakāpei būtu “jāizlozē” vienības katras grupas ietvaros. Bet, tā kā vienību sakārtojums grupu ietvaros ir nejaušs, nebūs liela kļūda, ja izlasē iekļausim no visām grupām vienus un tos pašus numurus. Nolasām gadījumskaitļu tabulā pirmos divus, kas mazāki vai vienādi ar 5. Tie ir 4 un 2.

 

 

 

 

 

            Katrai ģenerālkopas vienībai varbūtība nonākt grupā, no kuras izlozes otrajā pakāpē atlasīs izlases vienības, ir:

 

                        ,

 

            kur  k - atlasāmo grupu skaits (5),

                   K - visu grupu skaits (10).

 

            Ja kopas vienība jau ir nonākusi grupā, no kuras otrajā pakāpē ņem izlasi, tad varbūtība, ka viņa tiks izlozēta, otrajā pakāpē, ir:

 

                        ,

           

            kur  m - atlasāmo vienību skaits no grupas (2),

                   M - vienību skaits grupā (5).

 

            Varbūtību, ar kādu izlozētā saimniecība nonāk izlasē, nosaka abu iepriekšējo varbūtību reizinājums

 

                        .

 

            Līdz ar to varam aizpildīt 5.6. tabulu. Pirms tālākiem aprēķiniem jāpārbauda, lai , uzdevumā 50.

 

5.6. tabula

Divpakāpju gadījumizlase no 5.5 tabulas

 

i
37	17	0,2	5	85
12	0,6	0,2	5	3
33	13	0,2	5	65
48	100	0,2	5	500
50	140	0,2	5	700
40	20	0,2	5	100
20	1	0,2	5	5
14	0,7	0,2	5	3,5
7	0,4	0,2	5	2
3	0,2	0,2	5	1
S	-	-	50	1464,5

 

 

 

            Iegūtais ģenerālkopas saimniecību zemes kopplatības vērtējums 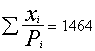 ha ir ievērojami lielāks nekā jau zināmais īstais lielums 1001 ha. Līdz ar to lielāks ir arī vidējais aritmētiskais (vidējā platība saimniecībā): vērtējums 1464,5 : 50 = 29,3 ha, īstenībā ģenerālkopā 20,0 ha.

            No šiem rezultātiem var izdarīt dažus metodiskus secinājumus.

1.     Stratificēta izlase, tāpat vienību atlase no sakārtotas (ranžētas) rindas dod daudz reprezentatīvāku izlasi nekā īsta vienpakāpes vai divpakāpju gadījumizlase.

2.     Vienkāršu gadījumizlasi tādēļ lieto samērā reti un tikai tad, ja par ģenerālkopas vienībām praktiski nav nekādu datu, lai tās stratificētu, ranžētu vai kā citādi uzlabotu izlasi.

3.     Pēdējā uzdevumā ļoti mazā 10 vienību divpakāpju gadījumizlase nedod iespēju sagaidīt daudz labāku rezultātu nekā ieguvām. Svērtais izlases aritmētiskais vidējais 29,3 atšķiras no ģenerālkopas vidējā 20,0 par 9,3 ha, kas, salīdzinot ar standartnovirzi svērtajā izlasē 46,8 un ģenerālkopā 33,1 ir mazs lielums. Iegūtie rezultāti pilnīgi atbilst varbūtību teorijas prasībām. Ja tie neapmierina praktiskās vajadzības, nedrīkst izmantot tik mazas izlases un praksē to arī nedara.

 

5.4. Vienkāršas gadījumizlases kļūdas un vērtējumu intervāli

 

            Ja ģenerālkopa nav novērota, interesējošo pazīmju parametri (aritmētiskie vidējie, relatīvie biežumi, variācijas rādītāji u.c.) nav zināmi. Parasti ir novērota tikai viena izlase no šīs ģenerālkopas, pēc kuras datiem ir aprēķināti to pašu interesējošo pazīmju rādītāji jeb statistiki (aritmētiskie vidējie, relatīvie biežumi, variācijas rādītāji u.c.). Jānovērtē, cik precīzi šie rādītāji raksturo atbilstošos ģenerālkopas parametrus; citiem vārdiem, kāda ir viņu izlases kļūda.

            Vispārējo nostādni parādīsim, vērtējot aritmētisko vidējo. Aritmētiskais vidējais ir pats svarīgākais katras kvantitatīvas pazīmes rādītājs. Bez tam citu rādītāju vērtēšana notiek diezgan līdzīgi.

            Izšķir aritmētiskā vidējā vērtēšanu ar skaitli (dažreiz saka : ar punktu) un ar intervālu.

 

5.4.1. Aritmētiskā vidējā vērtēšana ar skaitli

 

            Lietojot šo metodi, par nezināmā ģenerālkopas aritmētiskā vidējā vērtējumu pieņem vienu konkrētu skaitli. Tas ir izlases aritmētiskais vidējais, kurš aprēķināts pēc vienīgās reāli novērotās izlases datiem. Kā pierāda matemātiskā statistika, šis vērtējums atbilst četrām pamatprasībām. Vērtējums ir nenobīdīts. Tas nozīmē, ka izlases vidējais nav sistemātiski lielāks vai mazāks par nezināmo ģenerālkopas vidējo, bet vienkārši ar to neakrīt gadījuma apstākļu dēļ. Ja ņemtu vairākas tādas pašas izlases no tās pašas ģenerālkopas, izlašu vidējie svārstītos ap nezināmo ģenerālo vidējo. Vērtējums ir konverģējošs. Tas nozīmē, ka, palielinot izlases vienību skaitu, izlases un ģenerālkopas vidējo lielumu starpība samazinās. Tādā gadījumā izlases vidējais tiecas uz ģenerālo vidējo kā uz savu robežu. Vērtējums ir pietiekams, jo tas izmanto visu informāciju par sadalījuma centrālo tendenci pēc šīs pazīmes, kādu satur izlases dati. Vērtējums ir efektīvs, jo tam ir minimāla izlases kļūda, salīdzinot ar citiem centrālās tendences rādītājiem, piemēram, ar modu un mediānu.

            Tomēr izlases aritmētiskais vidējais ir un paliek gadījumlielums, kas ar ģenerālkopas vidējo nesakrīt. Jo nesakrīt pašas izlase un ģenerālkopa. Tādēļ, interpretējot un izmantojot izlases aritmētisko vidējo, jāņem vērā (jāuzrāda) tā izlases (reprezentācijas) kļūda.

            Izlases kļūdu, tāpat kā skaitļošanas kļūdu var izteikt gan absolūtās, gan relatīvās vienībās.

            Absolūto aritmētiskā vidējā izlases kļūdu izsaka tajās pašās vienībās kā pašu vidējo. Tajās pašās vienībās ir izteikti arī sākotnējie dati. Relatīvo kļūdu izsaka viena daļās vai procentos, rēķinot no aritmētiskā vidējā.

            Par aritmētiskā vidējā absolūtās kļūdas rādītājiem izmanto standartkļūdu (vidējo kvadrātisko kļūdu)  un robežkļūdu . Aritmētiskā vidējā standartkļūdu  aprēķina pēc īpašām formulām, kuras katram izlases veidam ir atšķirīgas. Robežkļūdu  aprēķina, pareizinot standartkļūdu  ar varbūtības koeficientu t (apzīmē arī ar ), kuru, atbilstoši brīvi izvēlētai varbūtībai p, nolasa normālā sadalījuma tabulās. Ja izlase ir maza (n < 50), jāizmanto t-sadalījuma (Stjudenta) tabulas. Līdz ar to:

 

                        .                                                                                                   (5.11)

 

            Relatīvās kļūdas rādītājs ir absolūtās kļūdas attiecība pret pašu aritmētisko vidējo, un to parasti izsaka procentos. Līdz ar to var aprēķināt divu veidu relatīvās kļūdas: pirmo, izejot no standartkļūdas, otro - no robežkļūdas.

 

                        ;             .                                                           (5.12)

           

            5.4. uzdevums. Rūpnīcā vienkāršas atkārtotas gadījumizlases ceļā ir izraudzīti novērošanai 100 strādnieki, un viņu aptaujas rezultātā noskaidrots, ka to vidējā izpeļņa ir 100 lati ar dipersiju 400. Aprēķināt vidējās izpeļņas absolūtās un relatīvās izlases kļūdas⁴.

 

            Analīze un atrisinājums.

            Tā kā ir ņemta vienkārša atkārtota gadījumizlase, jāizmanto šai izlasei specifiska aritmētiskā vidējā standartkļūdas formula (skat. 5.7. tabulu):

 

                        ,                                                                                                        (5.13)

 

            kur

                         - aritmētiskā vidējā standartkļūda,

                         - vidējā kvadrātiskā novirze (standartnovirze),

                         n   - vienību skaits izlasē.

 

            Lai izdarītu ievietošanu izlases standartkļūdas formulā, mums vispirms jāaprēķina izpeļņas standartnovirze. Tā ir kvadrātsakne no dispersijas:

 

                        (lati).

 

            Tālāk

 

                        (lati).

 

 

 

____________

⁴ Uzdevuma maksimālai vienkāršošanai ir ņemts pats vienkāršākais izlases veids un ērti, parocīgi skaitļi.

            Aprēķinātās vidējās izpeļņas 100 lati vidējā jeb standartkļūda ir 2 lati. Saskaņā ar varbūtību teoriju, ņemot citas tikpat lielas izlases no tās pašas ģenerālkopas 68% gadījumu nākošie izlases vidējie ir sagaidāmi 100 ± 2 lati robežās. Pēdējā teikumā jau iezīmējas vērtēšana ar intervālu, par ko runāsim turpmāk.

            Lai aprēķinātu aritmētiskā vidējā robežkļūdu, standartkļūda ir jāpareizina ar varbūtības koeficientu. Dažām biežāk lietotām varbūtībām lielas izlases gadījumā atbilst šādi varbūtības koeficienti (tos var atrast normālā sadalījuma tabulās):

 

Varbūtība	P	0,683	0,90	0,95	0,99
Varbūtības
koeficients	tP	1	1,64	1,962	2,583

 

            Ja izvēlamies varbūtību p=0,95, tad t=1,96 un  =1,96×2=3.92 (lati).

            Relatīvās kļūdas ir šādas:

 

                        %;       %,

 

tās ir izteiktas procentos no aritmētiskā vidējā.

            Izmantotā un citas biežāk lietotās formulas vienkāršas gadījumizlases kļūdu vērtēšanai ir sakopotas 5.7. tabulā.

 

5.7. tabula

Robežkļūdas vienkāršai gadījumizlasei

 

Izlases veids	Aritmētiskam vidējam	Relatīvam biežumam v
Atkārtota
Neatkārtota

 

 

5.4.2. Aritmētiskā vidējā vērtēšana ar intervālu

 

            Vērtējot ģenerālkopas aritmētisko vidējo ar vienu skaitli, šo vērtējumu īstenībā nevar saistīt ar kādu varbūtību. Varbūtība, ka izlases vidējais tieši sakritīs ar ģenerālo vidējo, būs galīgs skaitlis tikai tad, ja abus vidējos noapaļosim līdz kādai diskrētai vērtībai. Bet, paturot pietiekami daudz nenoapaļotu ciparu, tādas sakrišanas varbūtība ir niecīgi maza. Robežgadījumā tā ir nulle. Tādēļ, ja vērtējumu grib saistīt ar noteiktu varbūtību, interesējošais ģenerālkopas parametrs (piemēram, aritmētiskais vidējais) ir jāvērtē nevis ar vienu skaitli (punktu), bet ar intervālu. Netieši mēs to darījām jau iepriekšējā paragrāfā, pierakstot 100±2.

            Vērtējot aritmētisko vidējo ar intervālu, darbu izpilda un matemātiski pieraksta korektāk. Vērtējuma intervālu izveido, aprēķinot tā zemāko (apakšējo) un augstāko (augšējo) robežu, starp kurām ir sagaidāms ģenerālkopas aritmētiskais vidējais  ar vajadzīgo varbūtību. Intervāla robežas aprēķina, no izlases aritmētiskā vidējā atskaitot un tam pieskaitot aritmētiskā vidējā robežkļūdu:

 

                        .                                                                                (5.14)

 

Par šī intervāla pareizību varam būt droši ar to varbūtību, kāda tika izmantota, aprēķinot robežkļūdu. Pierakstot šo pašu intervālu ar standartkļūdu, iegūstam:

 

                        .                                                                            (5.15)

 

Ja pieņem t=1, tad par intervālu varam būt droši ar varbūtību 0,68, ja t=1,96 - ar varbūtību 0,95, ja t=2,58 - ar varbūtību 0,99 utt. (ja izlases nav maza).

 

            5.5. uzdevums. Aprēķināt pēc 1.uzdevuma rezultātiem strādnieku vidējās izpeļņas vērtējuma intervālu, par kuru varam būt droši ar varbūtību 0,95.

 

            Atrisinājums un tā novērtējums.

 . No tā seko, ka

 

                        ;

                        .

 

            Ar varbūtību 0,95 var apgalvot, ka šīs rūpnīcas strādnieku vidējā mēneša izpeļņa nav mazāka par 96,08 un nav lielāka par 103,92 latiem.

 

5.4.3. Nepieciešamā izlases lieluma aprēķināšana

 

            Šādu aprēķinu dažreiz lietderīgi izdarīt pirms izlases un statistiskās novērošanas. Aprēķiniem vajadzīgās formulas ir inversas formulām, kuras lieto jau izdarītās izlases raksturotāju (statistiku) robežkļūdu aprēķināšanai. Piemēram, ja grib izdarīt vienkāršu neatkārtotu gadījumizlasi, un galvenais rādītājs, kurš mūs interesē, ir aritmētiskais vidējais, tad formula ir šāda (skat. 5.8. tabulu).

 

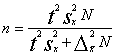                        ,                                                                                          (5.16)

 

kur simbolu nozīmes iepriekšējās. Praksē pirms izlases izdarīšanas un datu apstrādes parasti nav zināma interesējošās pazīmes dispersija . Te jāizlīdzas ar kāda analoga pētījuma rezultātiem vai, sliktākā gadījumā, ar ekspertīzes vērtējumu.

 

            5.6. uzdevums (turpina divus iepriekšējos).

            Cik strādnieki jāaptaujā par izpeļņu, ja vērtējam, ka izpeļņas standartnovirze varētu būt ap 20 latiem, un vēlamies, lai pēc izlases aprēķinātā vidējā izpeļņa neatšķirtos no vidējās izpeļņas ģenerālkopā vairāk nekā par 4 latiem, turklāt par to gribam būt droši ar varbūtību 0,95.

 

 

 

 

 

            Atrisinājums un komentārs.

            No uzdevuma izriet, ka , tātad = 400 ; = 4 , p = 0,95 , no kā seko, ka t = 1,96.

Tā kā ģenerālkopas strādnieku skaits N uzdevumā nav dots, jāizlīdzas ar vienkāršas atkārtotas gadījumizlases formulu. Jāņem vērā, ka šāds paņēmiens vienmēr ir tuvināts.

 

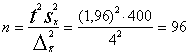                        (strādnieki).

 

            Lai izpildītu uzdevuma prasības, ir jāizvēlas ar īsti nejaušu izlasi un jāaptaujā 96 strādnieki. Vajadzīgais strādnieku skaits ir nedaudz mazāks nekā 1. un 2.uzdevumā, jo pieļāvām nedaudz lielāku aritmētiskā vidējā robežkļūdu: 4 lati pret aprēķinātajiem 3,92 latiem 1.uzdevumā.

 

5.8. tabula

 

Vienkāršas gadījumizlases nepieciešamais lielums

 

Izlases veids		Relatīvam biežumam v
Atkārtota
Neatkārtota

 

 

5.4.4. Relatīvā biežuma vērtēšana

 

            Relatīvā biežuma izlases kļūdas un vērtējuma robežas nosaka līdzīgi kā aritmētiskam vidējam, tikai alternatīvas pazīmes dispersiju rēķina ar specifisku formulu , kur v - relatīvais biežums izlasē.

            5.7. uzdevums. Mehāniskās izlases ceļā pie autoostas kases dažādās darba laika dienās un stundās aptaujāti 2000 pasažieri, aptaujājot katru desmito. No tiem 800 bija rīdzenieki. Aprēķināt, kādās robežās ir sagaidāms pasažieru - rīdzenieku īpatsvars visu pasažieru vidū. Vērtējuma robežām ir jābūt drošām ar varbūtību 0,99.

 

            Atrisinājums un komentāri.

            Pasažieru - rīdzenieku relatīvais biežums izlasē ir

 

                        jeb 40%.

 

            Varbūtības koeficients, kurš atbilst varbūtībai 0,99, lielas izlases gadījumā ir 2,58.

            Mehāniska izlase vienmēr ir neatkārtota.

Līdz ar to 5.7. tabulā var atrast vajadzīgo robežkļūdu formulu. Tā ir līdzīga vidējā aritmētiskā robežkļūdas formulai, ja ņem vērā, ka . Bez tam neatkārtota izlase ir reprezentatīvāka nekā atkārtota, ko atspoguļo reizinātājs ; robežgadījumā, ja n = N, tātad novēro visu ģenerālkopu, izlases kļūda kļūst nulle. Tātad:

 

            .

 

Vērtējuma robežas ir šādas:

           

            ,                                                                                      (5.17)

 

kur p - relatīvais biežums ģenerālkopā, varbūtība.

 

            0,4 - 0,026 < p < 0,4 + 0,026,

                     0,374 < p < 0,426.

 

Pasažieru rīdzenieku relatīvais biežums šajā autoostā nav mazāks par 0,374 jeb 37,4% un nav lielāks par 0,426 jeb 42,6%.

Izlases relatīvā robežkļūda ir

 

            .

 

Aprēķinātās izlases kļūdas, neskatoties uz lielu izlasi, iznāca samērā lielas tādēļ, ka izmantojām augstu varbūtību, kura atspoguļo nepieciešamo garantiju par atrastā intervāla pareizību. Ekonomikā parasti tik augsta varbūtība nav vajadzīga.

Ja relatīvais lielums ir ļoti mazs skaitlis (tuvs nullei) vai ļoti liels skaitlis (tuvs vienam), jālieto speciālas vērtēšanas metodes (skat. 5.6.3. paragrāfu).

 

5.4.5. Dažādu variācijas rindas rādītāju vērtēšana

 

Vairākus variācijas rindas rādītājus vērtē ar iepriekš aplūkoto metodi. Atšķiras vienīgi standartkļūdu aprēķināšanas formulas. Turklāt sarežģītākiem rādītājiem formulas dod tuvinātākus rezultātus, un to precizitāte vairāk atkarīga no zināmu priekšnoteikumu izpildes, piemēram, cik tuvs ir ģenerālkopas (arī izlases) sadalījums normālam sadalījumam.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5.9 tabula

 

Dažādu variācijas rindas rādītāju standartkļūdas vienkāršai gadījumizlasei

 

Vērtējamais rādītājs	Viņa standartkļūda
v
s²
s
k3
k3
k4
Me

 

5.9. tabulā k₃ - asimetrijas koeficients (trešās kārtas standartizētais moments), k₄ - ekscesa rādītājs (ceturtās kārtas standartizētais moments), Me - mediāna. Citi apzīmējumi iepriekšējie.

 

5.5. Izlases kļūdas dažiem citiem izlases veidiem

 

5.5.1. Stratificēta (tipoloģiska) izlase

 

            Ja ģenerālkopa ir sadalīta tipiskās grupās (strātās) un no katras grupas ir ņemta grupas lielumam proporcionāla īsti nejauša vai mehāniska izlase, tad izlases vidējā aritmētiskā standartkļūdu aprēķina līdzīgi kā vienkāršas gadījumizlases gadījumā. Tikai kopējās dispersijas vietā ņem grupu vidējo jeb intragrupu dispersiju . Līdz ar to aritmētiskā vidējā standartkļūda ir:

 

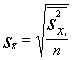                        .                                                                                                     (5.18)

 

Grupu vidējo jeb intragrupu dispersiju  aprēķina kā atsevišķu grupu dispersiju vidējo, par svariem izmantojot grupu lielumu (vienību skaitu tajās).

Lai iegūtu izlases robežkļūdu, standartkļūda, kā vienmēr jāreizina ar varbūtības koeficientu t.

Citas nepieciešamās formulas ir parādītas 5.10. tabulā.

Formulu lietošanas priekšnoteikums prasa, lai katras grupas ietvaros būtu ņemta īsti nejauša vai mehāniska izlase.

 

5.10. tabula

 

Stratificētas izlases robežkļūdas

 

Izlases veids	Aritmētiskam vidējam	Relatīvam biežumam v
Atkārtota
Neatkārtota

 

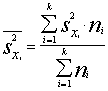                        ;                                                                                            (5.19)

 

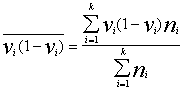                        ;                                                                         (5.20)

 

                        .                                                                                                      (5.21)                                      

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5.5.2. Sērijveida izlase

 

            Sērijveida izlases aritmētiskā vidējā un relatīvā biežuma robežkļūdu formulas ir parādītas 5.11. tabulā.

 

5.11. tabula

 

Sērijveida izlases robežkļūdas

 

Izlases veids		v
Atkārtota
Neatkārtota

 

Apzīmējumi

 

                        r - sēriju skaits izlasē,

                        R - sēriju skaits ģenerālkopā,

- starpsēriju dispersija.

 

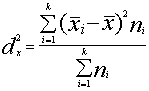                                                                                                           (5.22)

 

            Jāievēro, ka sērijveida izlases kļūdas nosaka starpsēriju jeb intersēriju dispersija, bet tipoloģiskās izlases - grupu vidējā jeb intragrupu (intrasēriju) dispersija. To summa ir pilnā jeb parastā dispersija

 

                        .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5.5.3. Divpakāpju izlase

 

            Divpakāpju izlases aritmētiskā vidējā un relatīvā biežuma robežkļūdu formulas ir parādītas 5.12. tabulā.

 

5.12. tabula

 

Divpakāpju izlases robežkļūdas

 

Izlases veids	Aritmētiskam vidējam	Relatīvam biežumam v
Atkārtota
Neatkārtota

 

            Bez iepriekš paskaidrotiem apzīmējumiem, - vienību skaits atlasītajās sērijās. Ja visās sērijās ir vienāds vienību skaits, tad .

            Zemsaknes pirmais saskaitāmais raksturo kļūdas kvadrātu, ko rada izlases pirmā pakāpe (sēriju atlase). Izteiksmes otrā daļa raksturo kļūdas kvadrātu, ko rada izlases otrā pakāpe (vienību atlase no jau atlasītajām sērijām).

 

5.6. Izlases kļūdas un normālais sadalījums

 

5.6.1. Normāli sadalīta gadījumlieluma un tā aritmētiskā vidējā vērtēšana

 

            Izlases kļūdu vērtēšana un vērtējuma apgabalu aprēķināšana balstās uz normālā sadalījuma likumu, bet mazas izlases gadījumā - uz tā modifikāciju t-sadalījumu (Stjudenta sadalījumu). Tā kā varbūtību teorijā un matemātiskajā statistikā normālā sadalījuma uzdevumus parasti risina, izmantojot citu risinājuma plānu nekā izlases metodē statistikas teorijā, ir nepieciešamas parādīt abu šo pieeju analoģijas, tādejādi padziļinot izpratni.

 

            5.8. uzdevums. Izmantojot 5.4. uzdevuma datus, aprēķināt ar varbūtību 0,95:

            1) kādā izpeļņas intervālā iekļaujas 95% strādnieku, ja intervālu ņem simetrisku pret vidējo. Citiem vārdiem, kādā intervālā ar varbūtību 0,95 var sagaidīt kārtējā strādnieka atbildi par viņa izpeļņu.;

            2) kāda ir aritmētiskā vidējā (100 lati) absolūtā izlases kļūda ar to pašu varbūtību un ģenerālkopas aritmētiskā vidējā vērtējuma apgabals?

 

Analīze un atrisinājums.

            Uzdevuma 1.jautājums ir parastais normālā sadalījuma netiešais uzdevums.

            Dots: =100; , no kā seko, ka s=20. No prasītās varbūtības izriet, ka F(t)=0,95. Izmanojot normālā sadalījuma tabulas, var atrast, ka t=1,96, ja vien izlase nav maza. Izmantojot grafisko analīzi (skat. 5.2. attēlu), pārējam no t skalas uz x skalu:

                        ;          x₁=100-39,8=60,2 lati,

 

;          x₂=100+39,2=139,2 lati.

 

 

 

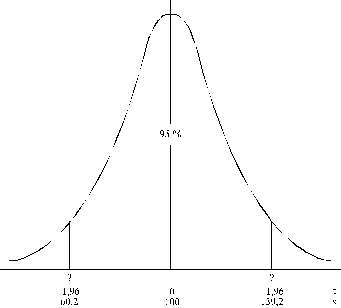
5.2 attēls. 8.uzdevuma 1.jautājuma grafiskā analīze

 

            Tātad apmēram 95% no strādniekiem saņem izpeļņu no 60 līdz 123 latiem. Šis intervāls atspoguļo strādnieku izpeļņas dažādību kā objektīvu parādību. Izlases lielums šo intervālu neietekmē. Tādēļ izlases vienību skaitu n=100 aprēķinos neņem vērā. Līdz ar to šādus uzdevumus parasti nesaista ar kursa nodaļu "Izlases metode".

            Uzdevuma otrajam jautājumam ir cits raksturs. Vairs nav runa par atsevišķu strādnieku izpeļņu, bet par kopas vidējo - vidējo izpeļņu. Jautājumu var traktēt tā: kādā intervālā ir sagaidāmi 95% vienāda lieluma izlašu vidējie, ja šādas izlases ņemtu atkārtoti no tās pašas ģenerālkopas? Iegūtu, piemēram, 98,31; 101,72; 102,03; 96,20 utt.

            Šeit jau darbojas lielā skaita likums. Kādas kopas novērojumu vidējais ir daudz stabilāks nekā atsevišķu novērojumu dati. Par cik lielāka ir šī stabilitāte, rāda vidējā aritmētiskā standartkļūdas formula. Ja izlase ir vienkārša gadījumizlase, atkārtota un pietiekami liela, tad formula, kā parādījām iepriekš, ir šāda:

 

                        ,

 

kur - izlases aritmētiskā vidējā standartkļūda,

       - pētāmās pazīmes standartnovirze.

Runājot par , to saucam par standartnovirzi jeb vidējo kvadrātisko novirzi (nevis standartkļūdu), jo tā atspoguļo variāciju kā objektīvu parādību. Pieņemam, ka "daba nekļūdās".  turpretī sauc par izlases aritmētiskā vidējā standartkļūdu, jo tā atspoguļo statistiķa kļūdu savas darbības - izlases metodes lietošanas rezultātā.

                        Uzdevumā (lati).

 

Šī kļūda ir atkarīga no izlases lieluma un tiecas uz nulli, ja izlases lielums tiecas uz bezgalību, resp. ģenerālkopas vienību skaitu.

            Atsevišķu strādnieku izpeļņas sadalījumu un vidējo izpeļņas sadalījumu var attēlot kopējā attēlā.

 

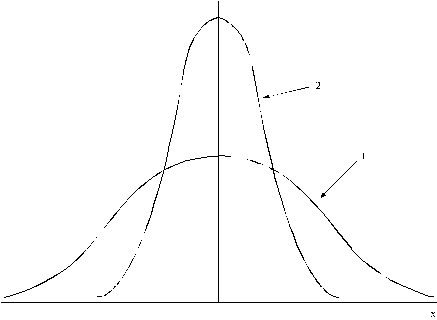
5.3. attēls. Sākotnējo datu un daudzu izlašu vidējo sadalījumi

 

                        1. x sadalījums, =20,

                        2.sadalījums, =2.

 

            Tādēļ vidējā lieluma vērtēšanu var izpildīt kā normālā sadalījuma uzdevuma netiešo tipu, tikai jāaizstāaj ar .

 

                        =100; =2; F(t)=0,95; no kā seko t=1,96;

 

                        ;           =100-3,92=96,08,

 

;          =100-3,92=103,92;

 

96,08 < m < 103,92 (lati).

 

Atbilde sakrīt aar 5.4.3. paragrāfā iegūto.

 

 

5.4. attēls Normālā sadalījuma netiešā uzdevuma grafiska ilustrācija

 

            Tātad vidējā izpeļņa ģenerālkopā ar varbūtību 0,95 atrodas intervālā no 96,8 līdz 103,8 latiem. Šis intervāls ir daudz šaurāks nekā paša gadījumlieluma intervāls, jo vidējais lielums ir stabilāks (noteiktāks), pateicoties lielā skaita likuma darbībai.

 

5.6.2. Gadījumlieluma intervāla varbūtības vērtēšana

 

            Izlases metodes uzdevumus var formulēt arī kā normālā sadalījuma tiešos uzdevumus.

 

            5.9. uzdevums. Saglabājot iepriekšējā uzdevuma datus, aprēķināt:

            1) varbūtību, ka kārtējā aptaujātā strādnieka izpeļņa atradīsies robežās no 80 līdz 120 latiem;

            2) varbūtību, ka, atkārtojot vienāda lieluma vienkāršu gadījumizlasi, aritmētiskais vidējais atradīsies robežās no 197 līdz 203 latiem. Citiem vārdiem, varbūtību, ka šajās robežās atradīsies ģenerākopas aritmētiskais vidējais.

 

Atrisinājums

            Pirmais jautājums ir parastais normālā sadalījuma tiešais uzdevums. Izdarām intervāla robežu standartizāciju:

 

            Atrodam prasīto varbūtību P(80 < x < 120) = F(1) = 0,68269 0,69.

5.5.attēls. 9.uzdevuma 1.jautājuma grafiska ilustrācija

 

            Par šo intervālu varam būt droši ar varbūtību 0,68. Citiem vārdiem, apmēram 68% strādnieku izpeļņa nav mazāka par 80 latiem un nepārsniedz 120 latus.

            Uzdevuma otro jautājumu risina līdzīgi, tikai uz ordinātu ass attēlā nav jāņem paša gadījumlieluma x skala, bet vidējo lielumu  skala⁵. Līdz ar to standartizācijas formulās  jāaizstāj ar :

 

                        ;

 

                        ;

 

                        ½t₁½=½t₂½=1,5;

 

                        P(197 <m < 203) = P(-1,5 < T < 1,5) = F(1,5) = 0,866390,97.

 

                       

 

 

 

 

 

 

 

 

 

 

 

__________________

⁵ Būtībā arī šīs skalas ir vienādas, jo vienādas ir x un  mērvienības. Atšķiras tikai pašas līknes, jo atšķiras x un  variācijas rādītāji.

m

 

5.6.attēls. 9.uzdevuma 2.jautājuma grafiska ilustrācija

 

 

Par šo apgabalu varam būt  droši ar varbūtību 0,87. Citā interpretācija: vadoties pēc izdarītās izlases datiem, var secināt, ka strādnieku vidējā izpeļņa ģenerālkopā nav mazāka par 197 un nav lielāka par 203 latiem ar varbūtību 0,87.

 

5.6.3. Relatīvā biežuma vērtēšana ja tas izlasē ir ļoti mazs vai ļoti liels skaitlis

 

            Izlases relatīvā biežuma vērtēšana, izmantojot tā standartkļūdu un robežkļūdu, un normālo vai Stjūdenta sadalījumu, ir pamatota tad, ja izlases relatīvais biežums ir tuvs apriori iespējamā definīcijas apgabala (0-1) vidum resp. 0,5. Ja relatīvais biežums izlasē ir tuvs vienai no šīm robežām, minētā metode apmierinošus rezultātus nedod, tāpat kā, vērtējot korelācijas koeficientu, ja tas izlasē ir tuvs 0 vai 1.

 

            5.10. uzdevums. Izdarot 100 pasažieru izlases veida kontroli autobusā, izrādījās, ka 2 no tiem brauc bez biļetes. Aprēķināt, kāds ir bezbiļetnieku īpatsvara vērtējuma intervāls ģenerālkopā ar varbūtību 0,95.

 

            Tradicionālais atrisinājums

 

                        .

 

                                    0,02 - 0,0273 < p < 0,02 + 0,0273

 

                                             -0,0073 < p < 0,0473.

 

            Zemākā robeža ir negatīvs skaitlis, kas nevar būt, jo iziet ārpus relatīvā biežuma (varbūtības) definīcijas apgabala. Lai šo pretrunu pārvarētu, atrod relatīvā biežuma v funkcijas j, kura sadalījums ir aptuveni simetrisks un tuvs normālajam, ar sekojoši inverso pāreju. R.Fišers šim nolūkam ir ieteicis funkciju

 

                        , kur v jāuztver kā lielums, kas izteikts grādos.

 

            Piemērā j no 0,02 ir

 

                       

 

Šīs funkcijas standartkļūda

 

                        ,

 

bet robežkļūda .

Funkcijas j vērtējuma robežas

 

                        0,2838 - 0,196 < F < 0,2838 + 0,196

 

                                     0,0878 < F < 0,4798.

 

 

Atliek izdarīt inverso pāreju uz v resp. p ar formulu

 

                        ,

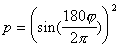kur sin arguments jāuztver kā izteikts grādos.

 

Ievietojot formulā secīgi j₁=0,0878 un j₂=0,4718, iegūstam p₁=0,00193; p₂=0,05646. Tātad

 

                        0,00193 < p < 0,05646,

 

kurš nav simetrisks pret izlases relatīvo biežumu 0,02. Metode nedarbojas pareizi, ja n ir ļoti mazs.