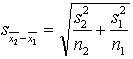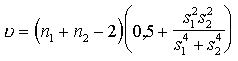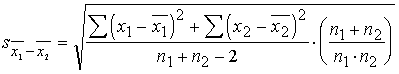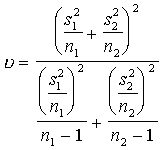6. Statistiskās hipotēzes

 

6.1. Uzdevuma nostādne

 

Analizējot statistikas datus, bieži ir jāsalīdzina divas statistiskās kopas vai vienas kopas divas daļas. Ja šo kopu vidējie lielumi vai citi analīzei nozīmīgi rādītāji atšķiras, tad parasti secina, ka atšķiras arī pašas kopas, kuras šie rādītāji raksturo.

Piemēram, kādā cehā izdarīja strādnieku darba ražīguma novērošanu. Izrādījās, ka rīta maiņā strādnieki izgatavoja vidēji 3,7 izstrādājumus maiņā, bet vakara maiņā - 3,5.

Varētu secināt, ka ir apstiprinājusies vispār pieņemtā  atziņa, ka rīta maiņā darbs ir ražīgāks. Tomēr tika reģistrēti daudzi gadījumi, kas ir pretrunā ar šo atziņu. Piemēram, pats ražīgākais strādnieks vakara maiņā deva 5,1 izstrādājumus stundā, bet pats neveiksmīgākais rīta maiņā - tikai 1,7.

Rodas jautājums, vai nelielu vidējo lielumu starpību šādos apstākļos var atzīt par statistiski nozīmīgu, vai var sagaidīt, ka tāda viņa būs arī turpmākos novērojumos, vai arī šādu atšķirību varēja izraisīt vienkārši nejaušības.

Tādēļ statistikas (arī ekonometrijas, biometrijas) uzdevums ir ne tikai konstatēt kādu rādītāju atšķirību, bet arī dot atbildi, vai šī atšķirība ir statististiski nozīmīga.

Jautājumu var formulēt arī citādi. Var jautāt, vai salīdzināmās grupas var uzlūkot par divām nejaušām izlasēm, kas ņemtas no vienas un tās pašās ģenerālkopas? Tad tās ir jāvērtē kā viens un tas pats statistisks (ekonomisks, sociāls, bioloģisks) tips, un grupu atšķirība jāvērtē kā nejauša. Ja tas nav iespējams, katra grupa pārstāv citu statistisku tipu, atšķirības ir būtiskas.

Šāda veida jautājumus izvirza un atbild, pārbaudot statistiskās hipotēzes.

Tā kā daļa novēroto faktu praktiski vienmēr hipotēzi apstiprina, bet daļā ir tai pretrunīgi, secinājumus nevar izdarīt absolūti, bet tikai ar noteiktu varbūtību.

Hipotēzes pārbaudes rezultātā ir jāpieņem kaut kāds lēmums, tādēļ šo statistikas nodaļu uzskata par statistisko lēmumu pieņemšanu.

 

Vēl daži statistisko hipotēžu piemēri.

 

1. Firma  pasūtīja  savas  produkcijas  reklāmu   televizijā. Pēc pārraides tika novērots neliels apgrozījuma pieaugums firmas veikalos. Vai tas ir statistiski nozīmīgs un reklāma ir attaisnojusies, vai atšķirības apgrozījumā varēja izraisīt vienkārši gadījuma apstākļi?

 

2. Veikals pasūta preci no divām vairumtirdzniecības bāzēm. Veikalvedim šķiet, ka viena no bāzēm pasūtījumus izpilda ātrāk. Vai tādi novērojumi ir statistiski nozīmīgi un turpmāk priekšroka būtu jādod šim vairumtirdzniecības uzņēmumam?

 

3. Mājsaimniecību budžetu statistikas dati rāda, ka mājsaimniecībās ar augstāku ienākumu līmeni ir caurmērā lielāks gaļas produktu un mazāks kartupeļu patēriņš, rēķinot uz vienu mājsaimniecības locekli, nekā mājsaimniecībās ar zemāku ienākumu līmeni (vidējie lielumi atšķirās). Tomēr ir arī daudz mājsaimniecību ar pretēju pārtikas produktu patēriņa tendenci. Rodas jautājums, vai pārtikas produktu patēriņa struktūra būtiski atšķirās grupās ar dažādu ienākuma līmeni, vai nē.

 

4. Izmēģinājumu saimniecību apstākļos šķirnes govīm ir augstāks piena izslaukums nekā bezšķirnes  govīm. Ir saprātīgi spriest, ka tāpat vajadzētu būt arī ražošanas apstākļos. Vai lauksaimniecības statististikas dati  apstiprina šo hipotēzi?

 

5. Strādājot pie konveijera, strādniekiem ir nepieciešamas šauri specializētas zināšanas un praktiskās iemaņas. Tomēr ir sapratīgi domāt, ka arī vispārējās izglītības līmenis ietekmē darba ražīgumu. Vai statistikas dati apstiprina vai noraida šo hipotēzi?

 

6. Bieži dzird apgalvojam, ka studentiem vīriešiem labāk padodas matemātikas priekšmetu mācīšanās, bet studentēm  sievietēm svešvalodas. Vai šajos priekšmetos iegūtās atzīmes  apsiprina tādus apgalvojumus?

 

6.2. Statistisko hipotēžu pamatjēdzieni

 

Par hipotēzi jēdziena plašākā nozīmē sauc zinātnisku pieņēmumu, kurš ir loģiski saprātīgs un ticams, tomēr prasa  tālāku pārbaudi, pierādījumus. Kad  tādi ir savākti, hipotēze kļūst par zinātnisku teoriju.

Statistiska hipotēze tāpat kā jebkura hipotēze ir zinātnisks pieņēmums. Tā izsaka spriedumus vai slēdzienus par statistiskiem faktiem, vai likumsakarībām. Hipotēze tuprmāk jāpārbauda un jāpamato.

Statistiskām hipotēzēm ir virkne īpatnību gan pēc satura gan formas.

Par statistisku hipotēzi sauc pieņēmumu par  statistiskās kopas vai divu kopu īpašībām. Statistiskās hipotēzes izvirza vai nu par atsevišķiem kopas parametriem, vai par  sadalījumu visumā. Statistisko hipotēzi pārbauda, salīdzinot hipotēzi ar datiem, kuri savākti tās pārbaudei. Parasti vienmēr daļa faktu hipotēzi apstiprina, bet daļa ir tai pretrunīgi. Tādēļ secinājumus var izdarīt tikai par kopu visumā. Bet tie nav attiecināmi uz visām tās vienībām.

            Turklāt secinājumiem ir varbūtības raksturs. Hipotēzes pārbaudes rezultātā atzīst par pieņemamu vienu no šādiem slēdzieniem:

 

            1. hipotēzi var pieņemt. Precizāk to pašu izsaka šādi: vairums novēroto faktu runā par labu

    hipotēzei, nav ar to pretrunīgi; hipotēzi nevar noraidīt.

 

            2. hipotēze ir jānoraida. Precizāk: vairums novēroto faktu nav savienojami ar hipotēzi.

 

Vienu vai otru no šiem slēdzieniem pieņem nevis absolūti, bet tikai ar zināmu iepriekš izvēlētu varbūtību, piem., 0,95. Ja fakti sadalās tā, ka nav pietiekama pārsvara hipotēzes pieņemšanai vai noraidīšanai, dažreiz pieņem trešo iespējamo slēdzienu:

 

            3. novērojumi ir jāturpina. Precizāk: ievērojama daļa faktu runā par labu, bet ievērojama daļa par sliktu hipotēzei, to nevar ne pieņemt, ne noraidīt ar pietiekami augstu varbūtību.

 

Lēmums par vienkāršu hipotēzi ir atkarīgs no viena rādītāja (parametra). Visbiežāk - no  aritmētiskā vidējā.

Piemēram, par hipotēzi, ka darbs rīta un vakara maiņā ir vienādi ražīgs, nepieciešamos datus dod strādnieku darba ražīguma novērojumi.

Ja šādu novērojumu būtu neierobežoti daudz, tad pat neliela darba ražīguma atsķirība pamatotu, kura maiņa ir ekonomiski izdevīgāka. Citiem vārdiem, mēs salīdzinātu divu ģenerālkopu vidējos, un konstatētu, ka  .

 

Šī starpība vienmēr būtu statistiski nozīmīga.

 

Reāli novērojumu skaits ir ierobežots un  bieži pat neliels. Tādēļ  mēs salīdzinām divas izlases un, konstatējot, ka , vēl nevar secināt, ka šī starpība ir nozīmīga, ka  tā saglabāsies arī turpmāk.

 

Tādēļ izvirzām hipotēzi, ka ģenerālkopā  jeb citādi

Šādu hipotēzi sauc par nulles hipotēzi un pieraksta šādi:

 

                                           

 

Datu par  un  lielumu nav. Ir tikai izlašu dati  un .

Aprēķinām šo lielumu starpību, parasti absolūtā izteikmē , iegūstot konkrētu skaitli, piem. 0,2.  Šī starpība būs nozīmīgāka tad, ja:

 

            1. abi vidējie aprēķināti pēc lielāku izlašu datiem, izmantojot lielu novērojumu  skaitu;

 

            2. variācija katras izlases ietvaros ir maza, novērojumi blīvi koncentrējas ap atbilstošo

    vidējo, un otrādi.

 

Grafiski vienkāršas nulles hipotēzes loģiku var ilustrēt šādi. Uz skaitļu ass atliekam abus vidējos  un . Ņemot vērā individuālo datu variāciju (retāk - arī asimetriju) konstruējam atbilstošos teorētiskos sadalījumos (parasti - normālos sadalījumus, 6.1. attēls).

 

 

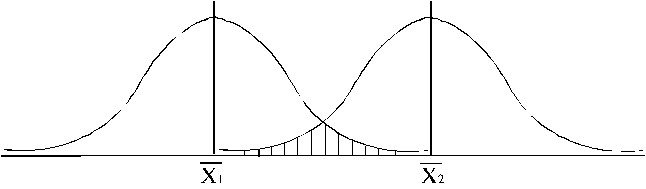
6.1 attēls. Divu normālo sadalījumu transgresija

 

Ja abi sadalījumi ievērojami pārsedzas jeb transgresē, tas runā par labu nulles hipotēzei, kura apgalvoja, ka ģenerālajās kopās abi vidējie ir vienādi: . Ja sadalījumi pārsedzas ļoti nedaudz, izvirzītā nulles hipotēze ir jānoraida :

 

.

 

Tātad lēmumu par nulles hipotēzi nosaka laukumu daļa, kas vienlaikus atrodas zem abām līknēm.

Lai izrēķinātu šī laukuma lielumu, būtu jāaprēķina abu līkņu krustošanas punkta abscisa. Praktiski šo hipotēzi pārbauda nedaudz citādi un tehniski vienkāršāk.

Lēmumi un slēdzieni, kas pieņemti, pārbaudot statistiskās hipotēzes, dažos gadījumos var izrādīties nepareizi, jo tie pamatojas uz varbūtību likumiem.

Tomēr, ja tie balstās uz pareizu parādību izpratni un to skaitlisku novērtējumu, pareizi lēmumi tiks pieņemti biežāk nekā kļūdaini.

Turklāt ir iespējams nodrošināt racionālu pareizu un kļūdainu lēmumu skaita attiecību.

 

6.3. Nulles hipotēze par divu aritmētisko vidējo starpību

 

Metodi ilustrēsim, izmantojot nodaļas sākumā doto piemēru par darba ražīgumu rīta un vakara maiņā.

Lai pārbaudītu izvirzīto statistisko hipotēzi, ir jāveic virkne loģisku un aritmētisku darbību,  kuras var sakārtot šādā secībā.

 

6.3.1. Hipotēzes formulēšana un tās pārbaudes priekšnoteikumu konstatēšana.

 

1.1. Lai pieņemtu lēmumu par divu aritmētisko vidējo starpības nozīmību, parasti hipotēzi formulē tā, ka apgalvo, ka abi salīdzināmie vidējie ģenerālkopā ir vienādi. Šādu hipotēzi var reducēt uz nulles hipotēzi  un viegli pārbaudīt.

Alternatīva hipotēze būtu apgalvojums, ka abi vidējie ģenerālkopā atšķiras: 

. Šādu hipotēzi uz nulles hipotēzi nevar reducēt un tās pārbaude ir sarežģīta.

Pirmajā skatījumā šķiet, ka abos gadījumos izvirzītās hipotēzes noraidīšana nozīmē alternatīvas hipotēzes pieņemšanu, tādēļ ir vienalga, kuru hipotēzi pārbauda.

Atšķirība veidojas tādēl, ka lēmumu par hipotēzi nepieņemam absolūti, bet ar noteiktu varbūtību, tātad rēķināmies, ka pieņemot lēmumu varam kļūdīties. Nulles un alternatīvās hipotēzes pārbaude paredz kontrolēt loģiski atšķirīgas kļūdas. Jautājuma dziļāka izpēte prasa noskaidrot, kādas kļūdas var pieļaut hipotēžu pārbaudē.

 

1.2. Jānovērtē, vai novērojumi abās salīdzināmajās kopās ir savstrapēji saistīti vai nē. Piemēra ietvaros - vai abās maiņās strādāja vieni un tie paši, vai citi strādnieki. Parasti strādnieki divas maiņas pēc kārtas nestrādā, tādēļ mūsu novērojumi ir nesaistīti.

Ja novērojumi būtu savā starpā saistīti, hipotēzes pārbaudei būtu iespējams piesaistīt papildus informāciju un lietderīgi izmantot modificētu shēmu.

 

1.3. Jānovērtē, vai:

 

            - abi salīdzināmie vidējie ir aprēķināti pēc vienādi lielu vai dažāda lieluma izlašu datiem,

   resp. vai  ;

            - vai pazīmes variācija abās kopās ir būtiski atšķirīga, vai nē (lai atbildītu uz šo

  jautājumu ir jāzina dispersija abās salīdzināmajās kopās, bet ja tā nav zināma, jāaprēķina).

 

Šajā apakšpunktā minētie priekšnoteikumi pamato formulu izvēli turpmākam darbam.

 

6.3.2. Hipotēzes pārbaudei vajadzīgo datu apstrāde

 

Lai pārbaudītu nulles hipotēzi par divu vidējo starpību, ir jāzina šie vidējie un ar tiem saistītās dispersijas (vai noviržu kvadrātu summas, vai standartnovirzes).

Uzsākot hipotēzes pārbaudi, šie lielumi var būt jau zināmi. Ja viņi nav zināmi, visprecīzākos rezultātus dod sākotnējo, negrupētu datu apstrāde (6.1.tabula). Mazāk precīzus, bet pieņemamus rezultātus iegūstam, apstrādājot grupētus datus (variācijas rindu, 6.2. tabula).

 

 

 

 

 

 

 

                                                                                                                                    6.1. tabula

 

Ceha strādnieku darba ražīgums rīta un vakara maiņā

(izstrādājumi vidēji stundā) novērojuma izdarīšanas dienā

 

Novērojumu (strādnieka) Nr.	1	2	3	4	5	6	7	8	9
Rīta maiņā	3,1	4,4	3,6	1,7	4,3	4,1	5,1	2,9	5,4
Vakara maiņā	3,6	2,6	5,1	4,0	3,1	3,8	3,4	4,4	3,9

 

10	11	12	13	14	15	16	17	18	19	20
4,0	2,7	3,7	2,3	4,0	2,8	4,6	3,9	3,7	3,4	4,1
2,9	3,3	1,7	3,7	4,2	2,8	-	-	-	-	-

 

                      

 

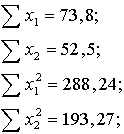
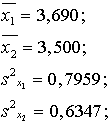
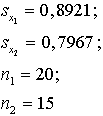
6.2.tabula

 

Ceha strādnieku darba ražīgums rīta un vakara maiņā (izstrādājumi vidēji stundā) novērojuma izdarīšanas dienā (grupēti dati)

 

Darba ražīgums,	Intervālu centri	Strādnieku skaits
izstrādājumi stundā	x	rīta maiņā	vakara maiņā
1,5 - 2,5	2	2	1
2,5 - 3,5	3	5	6
3,5 - 4,5	4	10	7
4,5 - 5,5	5	3	1
	-	20	15
	-	74	53
	-	288	195
	-	3,700	3,533
	-	0,7100	0,5156
	-	0,8426	0,7180

 

 

 

 

 

 

Piemērā iegūstam:

 

                                               

 

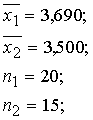
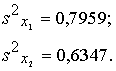
6.3.3. Empiriskā t koeficienta aprēķināšana

 

3.1. Empirisko t koeficientu aprēķina ar  formulu

 

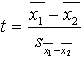                                ,                                                                                          (6.1)

 

kur   - vidējo lielumu starpības standartkļūda.

 

Parasti pieļauj, ka saskaņā ar nulles hipotēzei alternatīvo hipotēzi ģenerālkopā tiklab , kā    var būt lielāks. Tad var rēķināt un starpības absolūto vērtību, resp. un mainīt vietām. Speciālā gadījumā saskaņā ar alternatīvo hipotēzi ģenerālkopā viens vidējais noteikti ir lielāks par otru. Tas aprēķinus sarežģī.

 

Piemērā .

 

3.2. Darbietilpīgāka ir vidējo lielumu starpības standartkļūdas aprēķināšana. Šim nolūkam ir jāizvēlas viena no formulām, atbilstoši 1.3. punktā minētajiem priekšnoteikumiem. Formulas, no kurām izvēlēties, parasti sakārto tabulā (skat. 6.3. tabulu).

 

Piemērā vienību skaits kopās nav vienāds, jo  20   15 (strādnieku skaits maiņās).

 

Dispersijas  un  starpību uzskatīsim par statistiski nenozīmīgu.

 

Vēlāk aplūkosim, kā to noteikt precīzi. Līdz ar to lietojamā formula ir šāda:

 

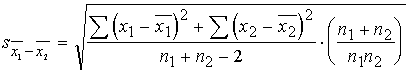                  (6.2)

 

Formulā ir paredzēts ievietot noviržu kvadrātu summas, bet mēs kā starprezultātus pierakstijām dispersijas. Tādēļ jāatceras, ka

 

,

 

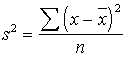no kā seko, ka

 

.

 

             6.3. tabula

 

Pamatformulas hipotēžu pārbaudei par divu aritmetisko vidējo atšķirības statistisko nozīmību

 

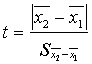
                             un var mainīt vietām

 

 

 

 

Izdarot ievietojumus, iegūstam, ka

 

 

 

 

 

 

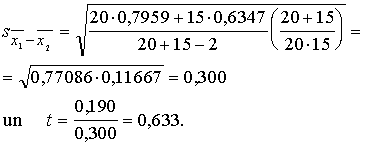
6.3.4. t koeficienta kritiskās robežvērtības atrašana un lēmuma pieņemšana

 

4.1. Lai noteiktu t koeficienta kritisko robežu, vispirms ekspertīzes ceļā jāizšķiras par varbūtību, kuru uzskatām par pietiekamu hipotēzes noraidīšanai.

Biometrijā kā standartus lieto varbūtības 0,95 un 0,99. Tās parasti izmanto arī matemātiskās statistikas demonstrējumos. Ekonomikas pētījumos šādas varbūtības šķiet augstas. Varbūt pietiktu 0,7 - 0,8, bet to grūti profesionāli pamatot.

Ja pieņemam varbūtību 0,95, tad atlikusī varbūtība 1 - 0,95 = 0,05 jeb 5% ir risks, izdarot slēdzienu, pieļaut pirmā veida kļūdu. Pirmā veida kļūdu pieļaujam, ja īstenībā pareizu hipotēzi (nulles hipotēzi) nepamatoti, kļūdas dēļ noraidām. Kļūda rodas tad, ja izlases dati nav reprezentatīvi.

Otrā veida kļūdu pieļaujam, ja pārbaudāmā hipotēze īstenībā ir nepareiza, bet kļūdas dēļ to atstājam nenoraidītu. Šo varbūtību nevar brīvi izvēlēties, bet var aprēķināt, ja ir izraudzīta pirmā veida kļūdas varbūtība. Tehniski tas ir sarežģīti, tādēļ parasti to nerēķina.

 

4.2. Jānosaka brīvības pakāpju skaits. Par brīvības pakāpju skaitu sauc kopas vienību skaitu n, pēc kura datiem aprēķināts empiriskais t koeficients, no tā atskaitot aprēķinos izmantoto saistošo nosacījumu skaitu.

Salīdzinot divus aritmētiskos vidējos, ir divi saistošie nosacījumi. Resp., lai divas reizes lietotu dispersijas aprēķināšanas formulu, tajā ir jaievieto divi vidējie. Ja ir fiksēti šie vidējie, tad visi novērojumi var būt jeb kuri skaitļi (brīvi), bet pēdējiem diviem (katrā kopā pa vienam) ir jābūt tādiem, lai nodrošinātu atbilstošu vidējo. Tātad

 

                              .                                                                                     (6.3)

 

Piemērā

 

                              .

 

4.3. Speciālās matemātiskās tabulās nolasa izvēlētās pirmā veida kļūdas varbūtību un esošam brīvības pakāpju skaitam atbilstošo t koeficienta kritisko robežu

 

                              .

 

Kritiskās robežas skaitlis ir lielāks, ja ņemam lielāku hipotēzēs pārbaudes varbūtību, resp., mazāku pieļaujam pirmā veida kļūdas risku.

Kritiskās robežas skaitlis ir mazāks, ja ir lielāks brīvības pakāpju skaits, citiem vārdiem, hipotēzes pārbaudē ir izmantoti vairāk novērojumu.

 

3.5. Salīdzina empirisko t koeficientu ar tā kritisko robežu un pieņem lēmumu.

 

Ja  ,

 

nulles hipotēzi noraida ar prasīto varbūtību.

 

Ja ,

 

nulles hipotēzi ar prasīto varbūtību nevar noraidīt. Tā paliek spēkā, vidējā atšķirība nav statistiski nozīmīga.

 

Piemērā  t = 0,633;   tātad  un darba ražīguma atšķirības statistiskā nozīmība rīta un vakara maiņā paliek nepierādīta. Faktiski novēroto atšķirību var izkaidrot arī ar izlases kļūdu.

Konkrētajā gadījumā samērā atšķirīgi vidējie nedeva iespēju noraidiīt nulles hipotēzi tādēļ, ka:

 

                        -novērojumu (strādnieku) skaits ir mazs;

                        -ir liela iekšgrupu variācija (atsevišķu strādnieku darba ražīgums abu grupu ietvaros

  ir ļoti atšķirīgs).

 

Studenti diezgan bieži kļūdās darba pēdējā punktā, pieņemot lēmumu, jo neatceras, kura no nevienādībām pie kāda lēmuma ved. To arī  no galvas mācīties nav vajadzīgs. Šaubu gadījumā ir jāatceras empiriskā t koeficienta formula (vienkāršotā pierakstā)

 

 

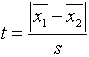
Ja starpības standartkļūdu (saucējā) pieņem par konstantu, tad t ir lielāks, ja lielāka ir vidējo starpība. Ja starpība ir liela, ir skaidrs, ka nulles hipotēze jānoraida, ja maza - nav pamata to noraidīt. Tātad liels empiriskais t koeficients ved pie hipotēzes noraidīšanas un otrādi.  Kritiskā robeža kalpo vienīgi tam, lai novērtētu kādu t uzskatīt par ‘’lielu’’ un kādu par ‘’mazu’’.

Ja empiriskais t iznāk mazāks par vienu, nav pat nepieciešams tabulās meklēt kritisko robežvērtību, jo ne ar vienu parasti izmantojamo varbūtību nulles hipotēzi noraidīt nevar.

Ja empiriskais t koeficients nedaudz pārsniedz vienu, nulles hipotēzi nevar noraidīt ar biometrijā lietotām varbūtībām 0,95 vai 0,99, bet to, atkarībā no brīvības pakāpju skaita, var noraidīt ar mazāku drošību - varbūtību 0,6 - 0,8, kas ekonometrijas pētījumos dažreiz ir pietiekami. Ja empīriskais t pārsniedz 3-4, nulles hipotēzi var noraidīt ar augstu varbūtību.

 

6.4. Nulles hipotēzes pārbaude par divu dispersiju starpību

 

Nulles hipotēzi  pārbauda vairāku uzdevumu risināšanai:

 

            1. lai izvēlētos piemērotas formulas divu aritmētisko vidējo starpības nozīmības pārbaudei.

    Iepriekš to izdarījām ekspertīzes ceļā bez aprēķiniem;

            2. lai dotu atbildi par  pašu dispersiju atšķirību nozīmību, ja pazīmes variācijai ir būtiska

                nozīme pētījumā;

            3. lai salīdzinātu iekšgrupu un starpgrupu dispersijas, tādējādi noskaidrojot, vai

                grupējums ir izdalījis raksturīgus ekonomiskus (sociālus, bioloģiskus) tipus. Šādu

                uzdevumu risina dispersijas analīze.

 

Nulles hipotēzes pārbaude par divu dispersiju starpību ir daudz vienkaršāka nekā par divu aritmētisko vidējo starpību, kaut gan visumā saglabājas tie paši izpildāmā darba soļi.

 

            1. Ir jāaprēķina abas salīdzināmās empiriskās dispersijas  un , ja tās nav dotas tieši.

    Aprēķini kļūst precīzāki, ja turpmāk lieto šo dispersiju nenobīdītos vērtējumus.

 

 

 

Tos aprēķina ar formulu

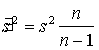                                                        .                                                                          (6.4)

 

 

            2. Atrod empirisko F attiecību (Fišera attiecību), dalot lielāko no

              salīdzināmajām dispersijām ar mazāko :

 

                                                        lielākā izlases dispersija

                        F   =                       -------------------------------  .                                                    (6.5)  

                                                        mazākā izlases dispersija

 

            3. Nosaka katras dispersijas brīvības pakāpju skaitu. Ja salīdzina divu grupu parastās, jeb

    pilnās dispersijas, tad   un .

 

Ja salīdzina iekšgrupu un starpgrupu  dispersijas, tad iekšgrupu (jeb grupu vidējai, jeb intragrupu) dispersijai ir  brīvības pakāpes, kur k - grupu skaits, bet starpgrupu (intergrupu) dispersijai  brīvības pakāpes.

 

4. Vadoties no hipotēzes pārbaudei izvēlētās varbūtības un brīvības pakāpju skaita, matemātiskās tabulās atrod F attiecības kritisko robežu .

Parastajos tabulu krājumos F kritiskās robežas ir tabulētas diviem nozīmības līmeņiem 0,05 un 0,01, kas dod iespēju noraidīt nulles hipotēzi ar varbūtību 0,95 un 0,99.

Tabulas ir šahveida. Kritiskais skaitlis ir jānolasa ailes un rindas krustojumā esošā rūtiņā. Jāņem aile, kuras galvā ir uzrādīts lielākās dispersijas brīvības pakāpju skaits , un rinda, kuras galvā uzrādots mazākās dispersijas brīvības pakāpju skaits .

 

5. Izdara salīdzināšanu un pieņem lēmumu. Ja empiriskā F attiecība ir lielāka

    par kritisko robežu , t.i.

                                                    

 

                                                  ,

nulles hipotēzi, kas apgalvo, ka salīdzināmās dispersijas neatšķiras būtiski, noraida ar izvēlēto varbūtību. Ja

 

,

 

šādu nulles hipotēzi ar prasīto varbūtību noraidīt nevar. Abu dispersiju atšķirība var būt radusies izlases kļūdu rezultātā.

Iepriekšējā piemērā par darba ražīgumu rīta un vakara maiņā aprēķinātās dispersijas bija   , kuras iegūtas novērojot pirmajā grupā , otrajā   strādniekos.

 

Pārbaudīsim, vai šīs dispersijas atšķiras statistiski nozīmīgi ar varbūtību 0,95.

 

 

 

            1. Dispersiju nenobīdīti vērtējumi

 

                                               

 

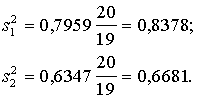
            2. 

 

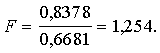
            3.  .

 

 

            4. Tabulas fragments

                       

	2,388

 

            5. 1,254 < 2,388  resp.  un nulles hipotēzi ar prasīto varbūtību noraidīt nevar. Novērotā dispersiju starpība varēja rasties izlases kļūdu rezultātā.

Iepriekš pieņemtais ekspertīzes lēmums ir bijis pareizs.

 

6.5. Hipotēzes pārbaude par ik pa pāriem saistītu novērojumu aritmetisko vidējo starpību

 

6.5.1. Uzdevuma nostādne un piemērs

 

Izvērtējot speciāli organizētu izmēģinājumu un eksperimentu rezultātus, ir raksturīgi, ka katram novērojumam izmēģinājuma apstākļos ir iekārtots atbilstošs novērojums t.s. kontroles apstākļos. Piemēram, lai pārbaudītu, vai kāds jauns minērālmēslojuma veids būtiski ietekmē ražību, iekārto vairākus paralēlus izmēģinājumu lauciņus. Katrā pārī vienā lauciņā lieto parbaudāmo vielu (tas ir izmēģinājuma lauciņš šaurā nozīmē), bet otrā - nē (kontroles  lauciņš). Visus pārējos apstākļus paralēlajos lauciņos cenšas saglabāt vienādus. Pēc tam aprēķina vidējo ražību atsevišķi izmēģinājuma un kontroles lauciņos, un ir jānovērtē, vai vidējo lielumu atšķirība ir statistiski nozīmīga.

Tādā pat veidā ir iespējāms organizēt arī pasīvos novērojumus, piemēram, aptaujājot vienus un tos pašus respondentus pirms un pēc cenu paaugstināšanas.

No statistikas metožu viedokļa mums ir divas izlases, kuras savstarpēji saistītas tā, ka katram novērojumam vienā izlasē atbilst viens noteikts novērojums otrā izlasē.

 

Iepriekš aplūkotās metodes nulles hipotēzes pārbaude par divu vidējo starpību šādu priekšnoteikumu neparedzēja. Abas salīdzināmās izlases domājām kā nejaušas, bez garantijas, ka katram novērojumam vienā izlasē atbilst noteikts novērojums otrā izlasē.

Ja mums ir ik pa novērojumu pāriem saistītas izlases, var izmantot parasto nulles hipotēzes pārbaudes shēmu, kas bija parādīta iepriekš. Tikai tā nav efektīva. Lietojot vispārējo shēmu, par neizskaidroto variāciju iznāk uzskatīt arī variāciju starp novērojumu pāriem, kura var būt liela. Ja novērojumi ir ik pa pāriem saistīti, šo variāciju var neņemt vērā, resp., izslēgt. To izdara, lietojot speciālu paņēmienu, kuru aplūkosim turpmāk.

Tādēļ, lietojot parasto paņēmienu, nulles hipotēze var palikt nenoraidīta un izmēģinājums atzīts par neveiksmīgu. Lietojot speciālo paņēmienu, kurš ievēro novērojumu savstarpējo saistību, var izradīties, ka nulles hipotēzi var noraidīt. Līdz ar to izmēģinājums kļūst nozīmīgs.

No tā var secināt arī, ka ik pa pāriem saistītie novērojumi ir informātīvāki nekā nesaistītie. Tādēļ tos plaši lieto dabas zinātnēs un zināmos gadījumos arī socioloģijā.

Kā pārbaudīt  nulles hipotēzi par ik pa pāriem saistītu novērojumu aritmētisko vidējo starpību, parādīsim, izmantojot ilustratīvu piemēru.

 

Piemērs. Agronomijas zinātne apgalvo, ka lupīnas sējumi bagātina augsni ar aktīvo fosforu. Lai vēlreiz pārbaudītu šo atziņu, veica augsnes  ķīmisko analīzi piecos laukos lupīnas dīgšanas un ziedēšanas periodā, skat. 6.4. tabulas pirmās trīs ailes.

 

6.4. tabula

 

Aktīvā fosfora saturs augsnē divās lupīnas attīstības fāzēs

 

	Aktīvā fosforskābe (mg) uz 100 g. augsnes		Novirzes	Noviržu kvadrāti
Lauka Nr.	dīgšanas stadījā	ziedēšanas stadīja
1	4,5	5,1	0,6	0,36
2	3,5	4,7	1,2	1,44
3	4,7	4,8	0,1	0,01
4	3,7	3,9	0,2	0,04
5	3,6	4,5	0,9	0,81
Summas	20,0	23,0	3,0	2,66
Vidēji	4,0	4,6	0,6	0,532

 

 

6.5.2. Rezultātu novērtēšana un nulles hipotēzes formulēšana

 

Izrēķinot aktīvās fosforskābes daudzuma aritmētiskos vidējos lupīnas dīgšanas stadījā    un ziedēšanas stadijā   redzam, ka pēdējais vidējais ir lielāks, kas sākotnēji apstriprina pārbaudāmo hipotēzi.

Lai apstiprinātu šīs starpības statistisko nozīmību, varētu izvirzīt un pārbaudīt parasto nulles hipotēzi , kur attiecīgos ģenerālos vidējos  un  reprezentē izlašu vidējie 4,0 un 4,6.

Taču jārēķinās, ka šādas hipotēzes pārbaudi traucēs ļoti nopietns blakus faktors: dabiskais jeb sākotnējais aktīvās fosforskābes saturs augsnē. Piemēram, pirmajā laukā tas ir relatīvi liels, bet otrajā un ceturtajā laukā - mazs. Šī dažādība, uz kuras fona notika izmēģinājums, var traucēt  pierādīt izmēģinājuma rezultātu nozīmību.

 

Īstenībā mūs interesē nevis fosforskābes absolūtais daudzums augsnē, bet tās pieaugums divās novērojumu reizēs: lupīnas ziedēšanas stadijā un dīgšanas stadījā. To atspoguļo novirzes

                                          ,                                                                               (6.6)

 

kas aprēķinātas 6.4. tabulas 4.ailē. Šīs starpības, atbilstoši teorijai, varam vērtēt, kā lupīnas pozītīvo iedarbību uz augsnes kvalitāti un tieši  par to nozīmību ir jāizvirza nulles hipotēze.

Tādēļ nulles hipotēze ir jāformulē šādi:

 

                                          ,                                                                            (6.7)

kur  - noviržu matemātiskā cerība, jeb vidējā novirze ģenerālkopā.

 

Izlasē to reprezentē  .

Izdarītie izmēģinājumi atbilst ik pa pāriem saistītu izmēģinājumu shēmai, jo katrā konkrētā laukā ar savām dabiskām īpašībām ir izdarīti divi novērojumi. Pirmais pirms izmēginājuma šaurā nozīmē (kontrole) un otrais - pēc izmēģinājuma saprotot to šaurā nozīmē.

 

6.5.3. Nulles hipotēzes pārbaude

 

Lai pārbaudītu izvirzīto nulles hipotēzi

 

                                         ,

 

ir jāizdara šādas darbības (darbību soļi apvienoti jeb agreģēti, salīdzinot ar pamatshēmu).

 

            1. Jāaprēķina empiriskais t koeficients

 

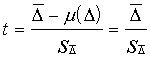                                          ,                                                                (6.8)

jo saskaņā ar hipotēzi ir nulle.

 

            1.1.    jau ir apēķināts tabulā, un tas ir 0,6.

 

            1.2. Lai aprēķinātu vidējās novirzes standartkļūdu, ir secīgi jāizmanto divas formulas:

 

            - jāprēķina noviržu dispersija, izmantojot vai nu definīcijas formulu

 

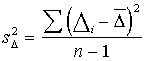                                                ,                                                           (6.9)

 

                        vai momentu formulu

 

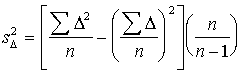                                         .                                         (6.10)

Abas šīs formulas ir vienīgi citiem simboliem pierakstītas parastās dispersijas formulas. Turklāt ir izdarīta korekcija ar brīvības pakāpju zudumu 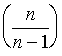, jo izlase uzdevumā ir ļoti maza, n = 5;

 

            -  jāaprēķina pati vidējās novirzes standartkļūda ar formulu

 

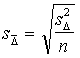                                               .                                                                            (6.11)

Izvēloties noviržu dispersijas aprēķināšanai momentu formulu, tabulas pēdējā ailē ir izskaitļoti noviržu kvadrāti un to summa, ko kopā ar noviržu summu varam ievietot formulā:

 

                                .

 

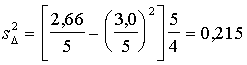Vidējās novirzes standartkļūda ir

 

                                         .

 

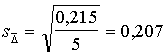Atgādinām, ka  ir vienkāršs variācijas rādītājs, bet  jau ir izlases kļūdas rādītājs.

 

            1.3. Aprēķinām empirisko t koeficientu:

 

                                              .

 

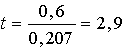2. Jāizvēlas hipotēzes pārbaudes varbūtība, resp., nozīmības līmenis, jāatrod tam un esošajam brīvības pakāpju skaitam atbilstošā t kritiskā robeža, empiriskais t jāsalīdzina ar šo robežu un jāpieņem lēmums.

 

            2.1. Izvēlamies biometrijā tradicionālo nozīmības līmeni , kas ir hipotēzes pārbaudē pieļaujamā pirmā kļūdas veida varbūtība.

 

            2.2. Brīvības pakāpju skaits ir

 

                                       

 

            2.3. t - tabulās (Stjudenta tabulās) atrodam, ka

 

                                  .

 

            2.4                        .

tātad izvirzīto nulles hipotēzi var noraidīt ar varbūtību, augstāku par 0,95. Lupīnas pozītīvā ietekme uz augsnes auglību ir izrādījusies statistiski nozīmīga.

 

6.6. Nulles hipotēzes pārbaude par divu relatīvo biežumu starpību

 

Pārbaudot nulles hipotēzi par divu aritmētisko vidējo starpību, t koeficienta kritisko vērtību atradām, izmantojot normālā sadalījuma likumu. Tā var rīkoties tādēļ, ka izlases aritmētiskie vidējie, daudzkārt atkārtojot izlasi, veido aptuveni normālu sadalījumu ap ģenerālkopas vidējo. Pirmais priekšnoteikums, kas to veicina, bet ne garantē, ir tas, ka aritmētiskais vidējais principā var būt jebkurš skaitlis. Izlases vidējais no ģenerālkopas vidējā vairumā gadījumu var novirzīties vienlīdz tālu kā samazināšanās tā palielināšanās virzienā.

Relatīvais biežums turpretī ir ierobežots skaitlis. Tas nevar būt mazāks par nulli un lielāks par vienu. Tādēļ relatīvajam biežumam ir ierobežots variācijas apgabals. Ja relatīvais biežums ģenerālkopā (varbūtība) turklāt ir tuvs vienai no šim robežvērtībām, tad izlases relatīvajiem biežumiem jāveido krasi asimetrisks sadalījums.

Piemēram, ja ņēmam daudz izlašu no ģenerālkopas, kur interesējošās pazīmes relatīvais biežums p = 0,01, tad pusē no izlasēm ir sagaidāms relatīvais biežums ļoti šaurā intervālā 0 - 0,01, bet otrā pusē - plašā intervālā 0,01 -1.

 

Tādēļ, lai pārbaudītu nulles hipotēzi par divu relatīvo biežumu starpību

 

                                    ,                                                                            (6.12)

 

tās vietā pārbauda hipotēzi                           

 

                                   ,                                                                             (6.13)

 

kur j ir funkcija no p, turklāt tāda, kuras sadalījums ir tuvs normālam.

R.Fišers ir pierādījis, ka šīm prasībām atbilst funkcija (p uztverts grādos):

 

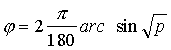                                                                                                     (6.14)

 

jeb                                 .                                                    (6.15)

 

Ar p apzīmējam relatīvo biežumu ģenerālkopā, resp., varbūtību. Turpmāk aprēķinos tā būs jāaizstāj ar relatīvo biežumu izlases: secīgi ar   un .

Nulles hipotēzi par to, ka divu izlašu relatīvo biežumu starpība neatšķiras statistiski nozīmīgi, pārbauda šādi.

 

1. Aprēķina empirisko t attiecību

 

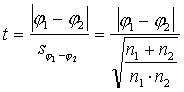                                   .                                                              (6.16)

Divu funkciju  un  starpības standratkļūda ir atkarīga vienīgi no novērojumu skaita salīdzināmajās izlasēs  un .

 

2. Ņemot vērā izraudzīto hipotēzes pārbaudes nozīmības līmeni  un brīvības pakāpju skaitu , t tabulās nolasa t kritisko vērtību. Salīdzina empirisko t ar tā robežvērtību un pieņem lēmumu.

 

Piemērs. Esam izrakstījuši tuvākajos pēcpensijas vecuma gados (55 - 64 g.) mirušo iedzīvtāju skaitu Latvijā un Zviedrijā¹.  Attiecinot to pret šī vecuma iedzīvotāju kopskaitu, izrādās ka mirstība Latvijā ir lielāka. Vai šī atšķirība ir statistiski nozīmīga?

 

6.5 tabula

Daži demogrāfijas rādītāji Latvijā un Zviedrijā

 

	Latvijā	Zviedrijā
Miruši 55 - 64.g. vecumā	6811	6920
Iedzīvotāju skaits 55  - 64.g. vecumā	306436	841386
Mirušo īpatsvars šajā vecuma grupā	0,02223	0,008224
	0,2993	0,1816

 

Aprēķinam  empirisko t attiecību

 

        

 

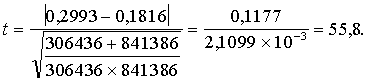
Praksē, ja rezuktāti iegūti pēc tik lielu statistisko kopu datiem, nulles hipotēzes parasti nemaz nepārbauda.

Iegūstot tik lielu t vērtību, nulles hipotēzi var tūliņ noraidīt ar vislielāko izvēlēto varbūtību. Ja ar hipotēzes pārbaudē iespējamo pirmā veida kļūdas varbūtību saprot laukuma daļu zem normālā sadalījuma līknes no perpendikula, vilktā punktā t = -55,8, un pa labi no perpendikula, vilktā punkta t = + 55,8, tad šī daļa ir atomāri maza. Publicētajās matemātiskajās tabulās to nolasīt  nemaz  nevar.

Tātad praktiski ar varbūtību 1 varam apgalvot, ka  pēcpensijas vecuma iedzīvotāju mirstība Latvijā ir lielāka nekā Zviedrijā.

Tik drošus secinājumus ieguvām tādēļ, ka  novērojumu (attiecīgā vecuma iedzīvotāju) abās  valstīs ir vairāki simti tūkstošu. Īstenībā šeit nav runa par divām izlasēm, bet divam ģenerālkopām.

Tagad pieņemsim, ka šie paši relatīvie  biežumi ir iegūti pēc mazpilsētu datiem, no kurām pirmajā ir 150, bet otrajā 200 attiecīgā vecuma iedzīvotāji. Jautājam, vai pēcpensijas vecuma iedzīvotāju mirstība pirmajā pilsētā ir būtiski lielāka nekā otrajā?

 

 

 

 

 

 

___________________

¹ Aprēķināts pēc ‘’Baltijas valstis un ziemeļvalstis. Statistisko datu krājums‘’. - R. : VSK 1996. -
  32., 35. - 36., 44. - 45. lpp. (1993.g. dati)

 

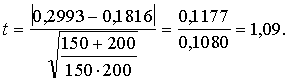
Izvēlamies hipotēzes pārbaudes varbūtību 0,95 , aprēķinam    .

 

Tabulās var atrast, ka .

 

Tātad    ,

un nulles hipotēzi nevar noraidīt pat ar samērā pieticīgo varbūtību 0,95. Mirstības starpību abās pilsētas var izskaidrot ar gadījuma faktoriem.

 

Varam secināt, ka statistisko hipotēžu pārbaude ir nepieciešama tad, ja salīdzināmo kopu raksturotāji ir iegūti pēc mazām izlasēm (daži desmiti - daži simti vienību).