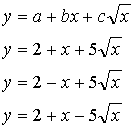Nelineārā regresija

10. Nelineārā regresija

10.1. Uzdevuma nostādne

Ekonomikā tāpat kā dabas un tehniskajās zinātnēs lielākā daļa korelatīvo sakarību ir nelineāras. Lineāras šīs sakarības parādās tikai tādēļ, ka interesējošā faktora reālās variācijas apgabals ir šaurs. Ir zināms, ka praktiski jebkura līkne, ja aplūko nelielu tās daļu, it tuva taisnei. Tādēļ lineāru regresijas vienādojumu ar labām sekmēm var lietot kā īstā, bieži nezināmā un nenosakamā modeļa tuvinājumu kādā nelielā viņa eksistences apgabalā.

10.1. attēls. Nelineāras sakarības šaurā intervālā ir tuvas lineārām

Piemēram, 10.1. attēlā sakarību eksistences apgabals ir no līdz . Ir redzams, ka šajā apgabalā līknes daļa ir tuva taisnei. Ja ņem vērā samērā lielo neizskaidroto variāciju, ar ko nākas samierināties praksē, tad līnijas liekuma raksturs parasti nav nosakāms. Tādēļ, vadoties no vienkāršības principa, pieņem, ka interesējošās sakarības pietiekami labi apraksta lineārs modelis.

Sakarību nelinearitāte ekonomiskā visbiežāk ir sekas tā saucamajam ''piesātinājuma efektam''. Ar to ir jāsaprot praktiski visu ražošanas faktoru atdevas samazināšanās, ja šo faktoru (resursu) daudzumi ir ļoti lieli un pārsniedz nepieciešamos. Piemēram, viegli iedomāties kādā laukā iestrādāt tādus minerālmēslojuma daudzumus, kas ne tikai neveicina augu attīstību, bet tos pilnīgi iznīcina.

''Piesātinājuma efekts'' nenozīmē, ka visos gadījumos ir kaut kādi ekonomikas attīstības ''griesti'', par kuriem augstāka attīstība nav iespējama. ''Piesātinājuma efekts'' nozīme tikai to, ka ražošanas tālāka attīstība, mehāniski palielinot un palielinot kādu līdz šim pozitīvi darbojošos faktoru, kļūst arvien neizdevīgāka un visbeidzot neiespējama. Šādā gadījumā ir nepieciešamas nevis kvantitatīvas, bet kvalitatīvas ražošanas tehnoloģijas izmaiņas. Turpinot piemēru par sakarību ''mēslojums - ražība'', ir nepieciešams radikāli uzlabot zemes kvalitāti un agrotehniku, pāriet uz augstražīgākām labības šķirnēm, varbūt arī izmantot efektīvākus mēslojuma veidus utt. Grafiski to var ilustrēt šādi (10.2. attēls).

10.2. attēls. 1. Kvantitatīvās sakarības pie patreizējās tehnoloģijas

2. Kvantitatīvās sakarības pie uzlabotas tehnoloģijas

Statistikas praksē nelineārus sakarību modeļus lieto tad, ja sakarību formu izdodas pietiekami labi pamatot, un tā nav lineāra.

Sakarības modelis, resp., vienādojuma tips, jāizvēlas un jāpamato pirms vismazāko kvadrātu metodes lietošanas. Tikai tad, kad vienādojuma tips ir izvēlēts, ar vismazāko kvadrātu vai citu metodi var atrast vienādojuma parametru vērtības.

Sakarību formu izraugās un pamato ar šādiem paņēmieniem.

1. Savā starpā saistīto ekonomikas kategoriju loģiski-profesionāla analīze. Lietojot šo paņēmienu, sakarību forma (modelis) ir jāpamato ar kvalitatīviem (loģiskiem) spriedumiem, bez skaitlisku datu izmantošanas.

2. Grafiskā analīze paredz izgatavot un novērtēt vizuāli korelācijas diagrammu. Ja punkti tajā negrupējas ap iedomātu taisni, tad ir jānovērtē, kādas nelineāras funkcijas grafiskajam attēlam tie ir vistuvāk, un par tālāko pētījumu modeli jāņem šī funkcija.

3. Mēģinājumu un salīdzinājumu paņēmiens paredz pēc vieniem un tiem pašiem datiem aprēķināt vairākus modeļus (regresijas vienādojumus) un tos salīdzinoši novērtēt. To var izdarīt tikai ar datortehniku. Par labāko un turpmāk lietojamo atzīst to modeli, kura parametrus vieglāk interpretēt un kuram ir augstāki sakarības ciešuma rādītāji.

Var būt gan vienkārši, gan daudzfaktoru nelineāri regresijas vienādojumi. Pēdējā gadījumā nav obligāti, lai visu faktoru sakarību forma ar rezultatīvo pazīmi būtu viena un tā pati; tā var būt dažāda. Tādā gadījumā veidojas samērā sarežģīti modeļi.

10.2. Vienkāršākie nelineārie modeļi

Ja, vadoties no profesionālām zināšanām, var pieņemt, ka pētāmās sakarības nav lineāras, tad jāizvēlas piemērota nelineāra funkcija. Parasti izvēli sāk, pārlūkojot vienkāršākās nelineārās funkcijas, kuras labi zināmas no algebras kursa. Arī viņu īpašības ir samērā vienkāršas. Tikai tad, ja arī tās konkrētam darbam izrādās nepiemērotas, aplūko speciālas funkcijas, kuras parasti ir sarežģītākas.

Kā vienkāršāko tūliņ aiz lineārās parasti aplūko kvadrātisko funkciju. Tā var būt vai nu nepilna

(10.1)

(10.2)

vai pilna

. (10.3)

Ekonometrijā kā modeli biežāk izvēlas pilno kvadrātisko funkciju.

Pilnā kvadrātiskā funkcija koordinātu sistēmas pirmajā kvadrantā labi modelē ekonomiskas sakarības, ja parametrs b ir pozitīvs, bet c - negatīvs skaitlis. Tādēļ grāmatās šīs zīmes nereti uzrāda jau modeļa vispārējā pierakstā. Tas nav īsti pareizi, jo parametru zīmes, tāpat kā skaitliskās vērtības aprēķina, apstrādājot konkrētus statistikas datus.

Kvadrātiskā funkcija atspoguļo ražošanas faktora mainīgu ietekmi uz rezultatīvo pazīmi. Modeļa definīcijas apgabala kreisajā pusē ietekme ir pozitīva un pakāpeniski, augot x vērtībām, samazinās. Modeļa ekstremālā vērtība raksturo faktora x daudzumu, kas nodrošina maksimālu rezultāta y daudzumu, kuru arī viegli aprēķināt. Vēl tālāk palielinot x vērtības, faktora ietekme uz rezultatīvo pazīmi ir negatīva. Faktors tādos daudzumos jau ir kaitīgs. (10.3. attēls).

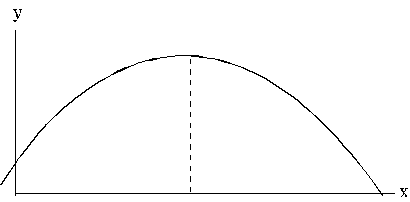
10.3. attēls. Kvadrātiskā funkcija (parabola)

Šāda modeļa īpašība labi saskan ar daudzu empīrisko sakarību īpašībām. Praksei mazāk piemērota ir cita modeļa īpašība - ka līknes kāpums un kritums abpus ekstremālās vērtības ir simetrisks.

Trešās un augstāku pakāpju polinomus ekonometrijā lieto reti. Šādos modeļos ir dadudz parametru, kas apgrūtina to aprēķināšanu. Tāpat, palielinot aprēķināmo parametru skaitu, ir nepieciešams vēl straujāk palielināt apstrādājamo sākotnējo datu masīvu, lai iegūtie parametri būtu statistiski nozīmīgi.

Biežāk ekonometrijas literatūrā ieteic apsvērt, vai interesējošo sakarību modelēšanai nav piemērota funkcija ar kvadrātsakni:

, (10.4)

, (10.5)

. (10.6)

Pilno funkciju ar kvadrātsakni attēlojošai līknei lielāks izliekums ir pie nelielām x vērtībām. Ja x vērtības ir lielas, šī funkcija asimptotiski tuvojas lineārai y = a +bx. Ja paramatru b un c zīmes ir pretējas, funkcija ir ekstremāla. Ja turklāt b un c vērtības skaitliski nav lielas, tad ekstrēms ir samērā tuvu koordinātu sākumam.

Vispār funkcijai ar kvadrātsakni nelinearitāte ir izteiktāka x mazo vērtību apgabalā, bet kvadrātiskai funkcijai - x lielo vērtību apgabalā.

10.1. tabula

Piemēri funkcijām ar kvadrātsakni

x

0	2	2	2
1	8	6	-2
2	11,07	7,07	- 3,07
4	16	8	- 4
6	20,25	8,25	- 4,25
9	26	8,0	- 4
25	52	2	2
100	152	- 48	52

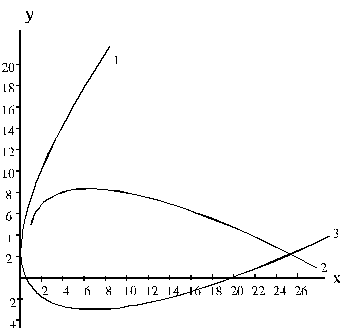
10.4. attēls. Funkcijas ar kvadrātsakni

(1. līkne)

(2. līkne)

(3. līkne)

Pie lielām x vērtībām šīs funkcijas tuvojas taisnēm:

1. y = 2 + x,

2. y = 2 - x,

3. y = 2 + x.

Tādēļ, apstrādājot datus, ir nozīme, kādās mērvienībās izsakām datus, piemēram, kilogramos vai tonnās. Otrajā gadījumā līkne atradīsies tuvāk koordinātu sākumam un tās izliekums būs lielāks, pirmajā - tālāk no tā un līkne būs tuvāka taisnei; aprēķinot taisni, šāda mērvienību maiņa rezultātus neietekmē.

No vienkāršo funkciju grupas ekonometrijā vēl plaši izmanto hiperbolisko funkciju

(10.7)

, (10.8)

. (10.9)

Biežāk izmanto otro nepilno formu ar parametriem a un c. Hiperbolas grafiskais attēls un īpašības arī ir zināmas no algebras kursa. Hiperbola ir samērā piemērota produkcijas pašizmaksas modelēšanai atkarībā no kāda faktora, kas izsaka ražošanas intensifikācijas līmeni.

Kaut gan iepriekš aplūkotās funkciju grupas ir vizuāli ļoti atšķirīgas un atšķirīgas ir arī to īpašības, tomēr tām ir arī kaut kas kopējs. Viņas pat var pierakstīt ar vienu izteiksmi. Lai to izdarītu, ir jāatceras, ka

Tātad visas minētās ir pakāpju funkcijas. Apzīmējot pakāpes rādītāju ar k, funkciju otro nepilno formu var izteikt šādi

. (10.10)

Izdarīt izvēli starp minētajām funkcijām īstenībā nozīmē dot skaitlim k kādu brīvi izvēlētu mazu, ērtu skaitlisku vērtību.

Tā kā izvēle jāizdara, vadoties no profesionāliem apsvērumiem, t.i. apriori, to nereti grūti pamatot. Tādēļ rodas vēlēšanās noteikt pakāpes rādītāju k aprēķinu ceļā, izmantojot vismazāko kvadrātu vai citu piemērotu metodi.

Tādā gadījumā kā faktiskās sakarības aprakstošo modeli izvēlamies pakāpes funkciju. Lai izvairītos no tehniskām grūtībām aprēķinu gaitā, parasti izvēlas šīs funkcijas nepilno formu:

(10.11)

jeb, parametrus apzīmējot ar alfabēta sākuma burtiem,

. (10.12)

Ja pakāpes rādītājs b ir robežās no 0 līdz 1, tad, pieaugot x vērtībām, pieaug arī y vērtības, bet atpaliekošos tempos. Šāda parādība ir samērā raksturīga dažādos ekonomikas procesos, un to sauc par piesātinājuma efektu. Tomēr pakāpes funkcijai nav ekstremālas vērtības, tātad faktora ietekme uz rezultatīvo pazīmi nevar būt negatīva jeb kaitīga pie kādām tās vērtībām.

Ja b ir lielāks par 1, tad rezultatīvās pazīmes pieaugumi apsteidz faktorālās pazīmes pieaugumus. Tādu parādību nereti novēro dzīves līmeņa pētījumos, kur izdevumi t.s. luksus preču iegādei tempu ziņā apsteidz iedzīvotāju ienākumus, jo šīs preces iegādājas tikai turīgāko iedzīvotāju slāņi.

Ja rezultatīvo pazīmi ietekmē ne tikai viens, bet vairāki faktori, tad ekonometriskajā modelī tos ietver vai nu ar vienādiem vai dažādiem pārveidojumiem¹.

Pilns kvadrātvienādojums diviem faktoriem būs

. (10.13)

Parametrus var apzīmēt arī ar vienu un to pašu burtu piešķirot tiem kārtas numurus.

Pilns modelis ar kvadrātsaknēm būs

. (10.14)

Pakāpju modelis diviem faktoriem vispārējā formā ir

. (10.15)

Ja faktoru skaits pāsniedz 2, tiklab kvadrātvienādojumā, kā arī vienādojumā ar kvadrātsaknēm, locekļu skaits ļoti strauji pieaug. Pieaug arī aprēķināmo parametru skaits. Tas padara šos modeļus praktiski neērtus.

Pakāpju modelim šī trūkuma nav. Palielinot faktoru skaitu, aprēķināmo parametru skaits pieaug atbilstoši faktoru skaitam tāpat kā lineārā daudzfaktoru modelī.

Pakāpju modeļa daudzfaktoru forma ir šāda :

. (10.16)

Tā ir būtiska šī modeļa priekšrocība. Pakāpju modelim ir arī vēl citas priekšrocības, kas nosaka viņa plašu izmantošanu ekonometrijā.

Šo modeli pirmie plašāk ir izpētījuši ārzemju autori Kobs un Duglass. Tādēļ ekonometrijas literatūrā to bieži sauc par Koba-Duglasa funkciju.

Modeļu konstrukcija pieļauj arī katram faktoram izvēlēties citu sakarību formu, piem.:

. (10.17)

Tādu izvēli izdara samērā reti, jo viņu parasti grūti pamatot.

______________

¹ Daudzfaktoru regresijai un korelācijai veltīta nākošā nodaļa, šeit aprobežojoties ar uzdevuma nostādni.

10.3. Sakarību formas izvēle

10.3.1. Sakarību formas profesionāla pamatošana

Drošākais sakarību formas pamatošanas paņēmiens ir pētāmo sakarību kvalitatīva analīze. Pieņemsim, ka ir jāaprēķina regresijas vienādojums, kas raksturo graudaugu ražības x ietekmi uz graudu pašizmaksu y. Var spriest tā. Visi izdevumi, kas saistīti ar graudu ražošanu, dalās mainīgos un pastāvīgajos izdevumos. Par mainīgiem sauc tos izdevumus, kuri mainās (pieaug) līdz ar produkcijas apjomu, piemēram, transporta izdevumi.

Apzīmējam ar

S₁ - graudu ražošanas izdevumu mainīgo daļu, ar

Q - graudu produkcijas apjomu (kopražu) un pierakstām, ka

_S1=a_{Q ,}(10.18)

kur a - pagaidām nezināms, vēlāk aprēķināms proporcionalitātes koeficients (normatīvs).

Tālāk ņemam vērā, ka ir nepieciešami tā sauktie pastāvīgie izdevumi ražošanas vispārīgo nosacījumu radīšanai. Lauksaimniecībā šie izdevumi ir propocionāli sējumu platībai un praktiski nav atkarīgi no ražības. Apzīmējot tos ar varam pierakstīt

, (10.19)

kur L - sējumu platība, bet b - pagaidām nezināms, vēlāk aprēķināms parametrs.

Tādējādi kopējos izdevumus var pierakstīt ar sakarību

(10.20)

Dalot abas puses ar Q (kopraža), iegūstam

, (10.21)

Tā kā = ,

tad, apzīmējot ar y pašizmaksu, bet ar x ražību, iegūstam

. (10.22)

Tātad sakarību "graudu pašizmaksa - ražība" var loģiski pamatoti modelēt ar hiperbolas vienādojumu.

Piemēram, pēc kāda saimniecību kopuma datiem (astoņdesmito gadu dati) esam ieguvuši, ka:

Vienādojuma brīvais loceklis (4,11) raksturo to graudu pašizmaksas daļu, kura nav atkarīga no ražības. Tas ir asimptotisks lielums, uz kuru tiektos graudu pašizmaksa,

ja izdotos neierobežoti palielināt ražību.

Hiperbolas vienādojuma koeficients (b = 117,5) raksturo izdevumus l ha graudaugu sējumu apstrādei - t.s. pastāvīgo izdevumu daļu. Rēķinot pašizmaksu, to dala ar ražību. Piemēram, ja ražība ir 10 cnt / ha, tad pie pašizmaksas jāpieskaita 11,75 rbļ., ja 20 cnt/ha, tad tikai 5,87 rbļ. utt. (grāmatas izdošanas laikā graudu pašizmaksu lauksaimniecības uzņēmumi rēķināja reti).

Jāatzīmē, ka sakarību formas loģiski - kvalitatīva izstrāde ir diezgan reti iespējama, it īpaši, ja runa ir par daudzfaktoru sakarībām.

10.3.2. Sakarības formas izvēle pēc korelācijas diagrammas

Šim nolūkam jāpārzina elementāro funkciju īpašības un grafiskie attēli. Ir lietderīgi ievērot sekojošo:

- ja faktorālās pazīmes absolūtajiem pieaugumiem atbilst rezultatīvās pazīmes vidējā lieluma aritmetiski proporcionāli pieaugumi, tad lieto lineāru vienādojumu;

- ja faktorālās pazīmes relatīviem pieaugumiem atbilst rezultatīvās pazīmes vidējā lieluma relatīvi pieaugumi, tad lieto pakāpes vienādojumu, to logaritmējot (lineāri logaritmisku vienādojumu);

;

- ja, pietiekami palielinot faktorālās pazīmes lielumu, rezultatīvā pazīme pret tā izmaiņām kļūst praktiski nejūtīga, paliekot vienā un tajā pašā līmenī, jālieto funkcija, kurai ir asimptota, piemēram, hiperbola;

- ja ir faktorālās pazīmes vērtības, pie kurām rezultatīvā pazīme ir maksimāla vai minimāla, jāizvēlas funkcija, kurai ir ekstrēms, piemēram, otrās kārtas parabola;

- ja sakarību eksistences apgabalā ir divi vai vairāki ekstrēmi (maksimums un minimums), jāizmanto trešās vai augstākas kārtas parabolas;

- ja līknes kāpums un kritums abpus ekstrēma nedrīkst būt simetrisks, jālieto lineāri logaritmiskas parabolas vai transcendentas funkcijas, piemēram, tā saucamā kinētiskā funkcija

. (10.23)

No apsvēruma, ka regresijas vienādojumu praktiski izmanto tikai noteiktā eksistences apgabalā, kurš bieži ir diezgan šaurs, izriet šādi praktiski noderīgi secinājumi:

- nelineāras sakarības vietā, kura pamatota loģiskas analīzes ceļā, var lietot lineāru sakarību, jo pētāmā apgabalā taisne atrodas pietiekami tuvu vajadzīgajai līknei;

- neekstremālu nelineāru sakarību modelēšanai dažkārt var izmantot kādu ekstremālas funkcijas, piemēram, parabolas, daļu.

Pēdējo paņēmienu plaši lieto tad, ja faktiskie dati par faktorālo pazīmi variē samērā šaurā apgabalā un apstrādājamā kopa ir neliela. Tādā gadījumā fiksēt kvantitatīvi līnijas liekuma raksturu vai nav iespējams vai ir nedroši. Tad lieto lineāru sakarības formu kā vienkāršāko. Bez tam šādā gadījumā vienkāršākā sakarības forma ļauj izvairīties no rupjām kļūdām.

Daudzfaktoru sakarību gadījumā nav tieši izmantojama grafiska analīze, jo viegli izveidot un novērtēt ir tikai pāru sakarību korelācijas diagrammu. Lietojot grafisko analīzi, parasti pieņem, ka daudzfaktoru sakarībām ir tā pati forma, kas pāru sakarībām. Kaut gan tāds pieņēmums var izrādīties arī nepareizs.

10.3.3. Izmēģinājuma modeļi

Ja aprēķinus izdara ar datortehniku, tad ir iespējams un dažreiz ir lietderīgi pēc vienas un tās pašas informācijas aprēķināt vairākus regresijas vienādojumus, piemēram, lineāru, pakāpes, parabolas u.c., un izvēlēties to, kurš praktiski labāk modelē interesējošās sakarības.

Izvēloties labāko vienādojumu, ievēro sekojošo:

- par labāku atzīst to modeli, kurš labāk atklāj pētāmo sakarību būtību, kuru vieglāk ekonomiski izskaidrot, resp., interpretēt;

- par labāku atzīst to modeli, kuram ir augstāki sakarību ciešuma radītāji;

- ja sakarību ciešuma rādītāji ir apmēram vienādi un arī ekonomiskās interpretācijas iespējas vienādas, izvēlas vienkāršāko modeli.

10.4. Linearizācija

Nelineāra regresijas vienādojuma parametrus pēc statistikas datiem parasti aprēķina, izmantojot t.s. linearizācijas metodi. Šī metode paredz izdarīt tādus sākotnēji izvēlētā modeļa pārveidojumus un argumentu maiņu (substitūciju), lai rezultātā iegūtu attiecībā pret aprēķināmajiem parametriem lineāru sakarību formu.

Piemēram, lai aprēķinātu hiperbolas

parametrus a un b, izmantojam jaunus mainīgos lielumus , tad varam rakstīt, ka

kurš formāli ne ar ko neatšķiras no lineāra pāru regresijas vienādojuma. Tikai aprēķinot krossummas, jāaceras, ka , līdz ar ko utt.

Ja vajadzīgās krossummas ir aprēķinātas pareizi, tālāk var izmantot parastās regresijas un korelācijas aprēķinu formulas un datorprogrammas. Pārejot pie rezultātu interpretācijas, ir jāizdara inversā (pretējā) substitūcija, atjaunojot sākotnējos mainīgos un nelineāro sakarību formu.

Otrs piemērs. Ir jāaprēķina pakāpes modeļa

(10.24)

parametri.

Lai modeli linearizētu, to logaritmējam

Apzīmējot

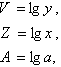
iegūstam

. (10.25)

kurš formāli ne ar ko neatšķiras no lineāra regresijas vienādojuma. Tikai krossummas jāaprēķina nevis pašiem datiem, bet to logaritmiem. Tādēļ var izmantot visas attiecīgās formulas un datorprogrammas. Pēc rezultātu iegūšanas ir jāizdara inversā substitūcija, ņemot vērā, ka , bet, ja ir izmantoti naturālie logaritmi, tad .

Trešais piemērs.

Loģiskās analīzes ceļā par nepieciešamo modeļa formu esam pamatojuši modificētu hiperbolu

. (10.26)

Ir nepieciešams aprēķināt parametru a un b skaitliskās vērtības.

Linearizāciju izdara šādi.

Ņem modeļa abu pušu apgrieztos lielumus

jeb

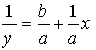, (10.27)

apzīmējot

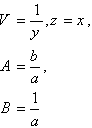
iegūstam modeļa linearizēto formu

Formējot krossummas normālvienādojumu sistēmai, jāievēro, ka rezultatīvās pazīmes tiešo datu vietā jāņem to apgrieztie lielumi.

Kad ar vismazāko kvadrātu metodi ir aprēķinātas parametru A un B vērtības, no tām iegūst sākotnējā modeļa parametru a un b vērtības, izmantojot inversus pārveidojumus :

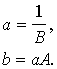
Plašāk lietotās nelineārās sakarību formas un viņu linearizācijas paņēmieni ir parādīti 10.2. tabulā.

10.2. tabula

Dažu biežāk lietoto modeļu linearizācija

Izvēlētais modelis	Pārveidojums	Substitūcijas
		V=	Z=	A=	B=
					b
			x
	----	y		a	b
		y		a	b
			x	a	b
			x	a	b
					b

Modelis pēc linearizācijas

Mainīgo lielumu pārveidojumi ir jāņem vērā, aprēķinot pēc sākotnējiem datiem normālvienādojumu sistēmai vajadzīgās krossummas. Parametru pāveidojumi jāņem vērā inversajā substitūcijā - pārējot no aprēķinātā linearizētā vienādojuma uz sākotnēji izvēlēto - nelineāro.

Ir jāatzīmē, ka visas nelineārās sakarības formas ( nelineārās funkcijas) šādā veidā linearizēt nav iespējams. Ja tā, tad šādu modeļu parametrus ar vismazāko kvadrātu metodi aprēķināt nevar. No nelinearizējamām sakarību formām ekonometrijā parasti izvairās. Ir pietiekami daudz viegli linearizējamu modeļu, starp kuriem var izvēlēties piemērotāko. Ja tomēr ir nepieciešams izmantot kādu nelinearizējamu sakarību formu, tad vajdazīgie parametri ir jāaprēķina ar kādu speciālu, parasti daudz sarežģītāku metodi.

10.5. Linearizācijas trūkumi

Ir jāņem vērā, ka, izdarot linearizāciju, mainās noviržu kvadrātu summas, kuras minimizē. Sevišķi spilgti tas izpaužas, ja kaut kādi pārveidojam rezultatīvo pazīmi.

Piemēram, linearizējot pakāpes funkciju, mēs tiklab faktorālo, kā arī rezultatīvo pazīmes logaritmējam. Tas nozīmē, ka tālākā darba gaitā tiek minimizēta nevis neizskaidrotā rezultatīvās pazīmes noviržu kvadrātu summa, bet šo datu logaritmu noviržu kvadrātu summa.

Tā kā izmaiņu raksturs pašiem datiem un to logaritmum ir atšķirīgs, vispārējā gadījumā pašu datu noviržu kvadrātu summas minimizācija un šo datu logaritmu noviržu kvadrātu summas minimizācija dod atšķirīgus rezultātus.

Prakse ir parādījusi, ka dažos gadījumos regresijas līnija, kas ir pārliecinoša logaritmiskajās skalās izveidotajā korelācijas diagrammā, nav pārliecinoša sākotnējās skalās izveidotajā korelācijas diagrammā. Tādēļ, izdarot aprēķinus ar linearizācijas paņēmienu, nedrīkst sagaidīt, ka rezultāti vienmēr būs profesionāli apmierinoši.

Ja izrādās, ka iegūtais modelis nav profesionāli apmierinošs, jāmeklē kāds cits šī modeļa parametru aprēķināšanas paņēmiens.

Kā izmainās modeļu parametri, mainot noviržu kvadrātu summas minimizācijas nosacījumus, viegli izsekot, ņemot ļoti vienkāršotus piemērus.

Pieņemsim, ka ir jāaprēķina viena parametra modelis, kuram šis parametrs turklāt nav saistīts ar faktorālās pazīmes vērtību, tātad

y=a

Izdarot vismazāko kvadrātu metodei raksturīgās operācijas,

, (10.28)

, (10.29)

(10.30)

Var pārliecināties, ka vislabākais a vērtējums ir aritmetiskais vidējais .

Pieņemsim tālāk, ka mums ir tikai divi novērojumi ar y vērtībām 1 un 10.

x vērtībām nav nozīmes, jo x izvēlētajā modelī neieiet.

Viegli redzēt, ka abu skaitļu vidējais ir

Tagad pamēģinām abus skaitļus logaritmēt, atrast logaritmu vidējo un to potencēt. Matemātikā tā rīkoties nav atļauts, bet analogas darbības paredz sakarību modeļu linearizācija.

Iegūtais rezultāts būtiski atšķiras no iepriekšējā.

Par linearizācijas radītiem izkropļojumiem varam pārliecināties arī izveidojot nedaudz sarežģītāku piemēru. Ņemam divus novērojumu pārus ar vienādām x, bet atšķirīgām y vērtībām, skat. 10.5. attēlu.

Loģiski sagaidāms, ka izlīdzinošā līkne ies caur abu novērojumu pāru y vidējiem (nepartrauktā līkne). Praksē, rēķinot, piemēram, pakāpes funkciju, līkne būs pietuvinātāka apakšējiem punktiem (pārtrauktā līnija).

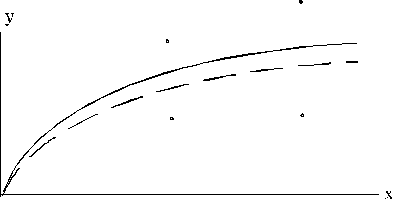
10.5. attēls. Linearizācijas radītā līknes nobīde.

Daudzi praktiski aprēķini ir parādijuši, ka minimizējot nevis pašu datu, bet to logaritmu noviržu kvadrātu summu, daudz lielāku nozīmi (svaru) iegūst novērojumi ar mazām y vērtībām. Izlīdzinošā līkne korelācijas diagrammā ir pietuvināta punktiem diagrammas lejasdaļā daudz vairāk, nekā tas būtu līkni novelkot vizuāli.

Izskaidrojums ir šāds. Visos gadījumos skaitļu logaritmi ir mazāki nekā paši skaitļi, Taču mazu skaitļu un to logaritmu atšķirības ir mazākas nekā lieliem skaitļiem un to logaritmiem. Tādēļ, izdarot noviržu kvadrātu minimizāciju logaritmiskā skalā, līkne tiek pietuvināta novērojumiem ar mazām rezultatīvās pazīmes vērtībām, bet attālināta no novērojumiem ar lielām rezultatīvās pazīmes vērtībām. Abu līkņu savstarpējās nobīdes ir lielākas, ja lielāka ir rezultatīvās pazīmes datu variācija.

Vai visos gadījumos ir raksturīgi, ka abi minimizācijas kritēriji dod atšķirīgus modeļa reizinātājus, bet vienādus vai maz atšķirīgus pakāpes rādītājus. Praktiskā pieredze ļauj secināt, ka var būt arī gadījumi, kad linearizācijas rezultāta iegūstam arī samazinātus pakāpes rādītājus.

Modeļa izkropļojumi ir mazāki, ja:

1. visi sākotnējie dati ir lieli skaitļi,

2. sakarību ciešums ir liels.

Izmantojot pirmo īpašību, var mēģināt ietvert modelī t.s. aprioro konstanti, resp., pirms logaritmēšanas visām y vērtībām pieskaitīt kādu lielu skaitli.

Turpinot iepriekšējo piemēru, abiem skaitļiem 1 un 10 pieskaitām 100; atrodam šo skaitļu vidējo un no tā atskaitām 100.

Šādu darbību rezultātā vidējais nav mainījies.

Tagad pamēģinam to pašu, izmantojot datu logaritmēšanu :

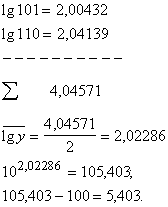
Pareizais vidējais joprojām nav iegūts, bet rezultāts ir tam daudz tuvāks, nekā iepriekš.

Tomēr apriorās konstantes ietveršana modelī problēmu neatrisina. Šada apriorā konstante pārceļ variācijas apgabalu tālu no koordinātu sākuma, kur aprēķināmā līkne jau ir ļoti tuva taisnei. Šāda rīcība gan novērš izkropļojumus, kas rodas linearizācijas rezultātā, bet iegūtais modelis vienīgi pēc formas ir nelineārs, bet pēc būtības lineārs.

Parastie linearizācijas paņēmieni ir matemātiski korekti tikai tad, ja sakarības ir funkcionālas. Tie ir pieņemami, ja sakarības ir ciešas, bet ir pilnīgi nederīgi, ja sakarības ir vājas.

Tādēļ var mēģināt uzlabot linearizācijas rezultātus, mākslīgi palielinot sakarību ciešumu. To izdara, rēķinot modeli nevis pēc sākotnējiem datiem, bet pēc rezultatīvās pazīmes grupu vidējiem lielumiem, piemēram, pēc deciļgrupējuma.

Šādi, rīkojoties pilnīgi pretēji klasiskās statistikas ieteikumiem, praksē esam ieguvuši no profesionalā viedokļa un no korelācijas diagrammas vizuālā vērtējuma ļoti labus modeļus.

Paņēmiena trūkums ir tas, ka nav iespējams aprēķināt sakarību ciešuma rādītājus ar momentu metodi. Formāli izrēķinātie sakarību ciešuma rādītāji šādā gadījumā ir ļoti augsti (korelācijas koeficients tuvs vienam), bet tas neatspoguļo reālo sakarību ciešumu. Izdarot grupēšanu pēc faktorālās pazīmes, mēs pilnīgi pazaudējam rezultatīvās pazīmes iekšgrupu variāciju, kura ir galvenā, kas nosaka sakarību ciešumu. Tadēļ formālie sakarību ciešuma rādītāji iznāk ļoti augsti.

Var pārliecināties, ka vēl lielāki modeļa izkropļojumi ir iespējami, ja linearizācijā izmanto apgrieztos lielumus.

Datorprogrammu paketes piedāvā aprēķināt dažādu modeļu parametrus ar t.s. iteratīvām metodēm. Viņu lietošanas praktiskā pieredze vēl ir maza. Var atzīmēt sekojošo:

- ir iespējama ne tikai viena, bet dažādas iteratīvās metodes;

- programmu aprakstos metodes algoritms parasti atklāts nepietiekami;

- metodes vājāk saistītas ar varbūtību teoriju nekā vismazāko kvadrātu metode.

Lietojot dažas iteratīvās metodes iedzīvotāju izdevumu funkciju aprēķinos, no profesionālā vērtējuma viedokļa ieguvām modeļus, kuri:

- parasti bija labāki, nekā deva vismazāko kvadrātu metode pēc sākotnējo datu logaritmēšanas;

- parasti bija sliktāki, nekā apstrādājot deciļgrupējuma datus ar vismazāko kvadrātu metodi un datu logaritmēšanu.

10.6. Mainīgo lielumu mērvienību maiņa

Dažos gadījumos vai nu datu savākšanas un apstrādes, vai modeļa interpretācijas stadijā rodas vēlēšanās izmainīt vai nu rezultatīvās vai faktorālās pazīmes mērvienību, piemēram svara mērvienību tonnās izteikt centneros vai otrādi.

Aplūkosim mērvienību maiņu pakāpju modelī.

Ja rezultatīvās pazīmes mērvienību grib izmainīt k reizes, tad pietiek ar šo konstanti pareizināt pakāpes modeļa labo pusi. Praktiski tas nozīmē pareizināt ar k modeļa reizinātāju (multiplikātoru).

Pieņemam, ka modelī

(10.31)

y bija izteikts tonnās, bet teorētiskos y lielumus gribam interpretēt centneros. Tad modeļa reizinātājs jāņem k reizes lielāks. Par to var pārliecināties, izdarot atkārtotus aprēķinus,

un . (10.32)

Ja faktorālās pazīmes mērvienību grib mainīt k reizes, bet rezultatīvo pazīmi saglabāt iepriekšējās vienībās, tad modeļa labā puse jāmaina reizes, kur b - modeļa pakāpes rādītājs:

. (10.33)

Piemēram, ja modelis aprēķināts, ņemot x tonnās, bet to grib interpretēt un tajā ievietot x vērtības centneros, tad modeļa labā puse jādala ar , jo visas tajā ievietojamās x vērības būs 10 reizes lielākas.

Arī par to var pārliecināties, izdarot praktiskus aprēķinus.