13.
Ievads ražošanas funkciju teorijā
13.1. Vispārčjas zišas par rażošanas funkcijām
13.1.1. Jēdziena izcelšanās
Ražošanas funkcijas kā ekonometrijas modeļu veids parādījās
praktiski vienlaikus ar ekonometrijas zinātni. Ražošanas funkciju rašanos bieži
saista ar K.Koba un R.Duglasa rakstu Ražošanas teorija (ASV, 1928).
PSRS un līdz ar to arī Latvijā ražošanas funkciju jēdziens
kļuva pazīstamāks pēc E.Hedī,
D.Dillona monogrāfijas Ražošanas funkcijas
lauksaimniecībā tulkojuma1. Latvijā pirmie pētījumi šajā novadā publicēti piecus
gadus vēlāk 2.
Enciklopēdiskajā vārdnīcā ražošanas funkcijas ir skaidrotas
šādi: Ražošanas funkcijas, metemātiskā formā izteiktas funkcionālas sakarības starp
saražotās produkcijas daudzumu un izlietotajiem resursiem (pirmā ražošanas
funkcija - Koba-Duglasa funkcija; izstrādāta ASV). Ražošanas funkcijas plaši izmanto
ekonomikas attīstības
matemātiskajos modeļos 3.
Ekonometriskajā literatūrā terminu ražošanas funkcijas
nesaprot tik viennozīmīgi. Tomēr sākotnējam priekšstatam enciklopēdijas
skaidrojums ir pietiekams. Par dažādām iespējamām niansēm runāsim turpmāk.
13.1.2. Rażošanas funkcijas un regresijas vienādojumi
Ražošanas funkcijas gan pēc satura, gan aprēķināšanas
metodēm, gan lietošanas specifikas ir jāuzlūko par vienu ekonometrijas modeļu
veidu. Tādēļ vispirms īsi jāraksturo, kas ir modelis zinātnē un ekonomikā.
Varam vēlreiz izmantot enciklopēdiju: Modelis lietišķajās zinātnēs ...
sakarību kopums, kas pētījamo procesu attēlo vienkāršotā veidā, aprakstot tās būtiskās pazīmes.
Modelēšana, objektu pētīšana ar modeļu palīdzību; izziņas metode. Dod varbūtējas zināšanas. Ekonomiski matemātiskie modeļi, ekonomiska procesa,
parādības vai objekta matemātisks apraksts (pasvītrojums - mūsu) 4.
Tagad mēģināsim norobežot ražošanas funkcijas no
radniecīgiem ekonometrijas modeļiem pēc sistematiskām pazīmēm.
1. Ražošanas funkcija ir sakarību modelis, kurš apraksta sakarību starp
produkcijas apjomu un patērēto resursu daudzumu. Šīs sakarības nekad nav
funkcionālas, bet ir korelatīvas. Tādēļ terminu ražošanas funkcijas nedrīkst saprast kā
funkcionālas sakarības matemātikas izpratnē. Galvenās ražošanas funkciju
parametru aprēķināšanas (identifikācijas) metodes ir korelācijas - regresijas analīze ar visām
viņas modifikācijām un papildinājumiem. Ražošanas funkcijas ir statistiski
(empīriski) modeļi pretstatā vairumam optimālās programmēšanas modeļu, kuriem
ir normatīvs raksturs. Tas nenozīmē, ka ražošanas funkcijas nevar izmantot
racionālu vai pat optimālu lēmumu pamatošanai.
Vēl jāaizrāda, ka termins ražošanas funkcijas nedrīkst
asociēties ar nozares, uzņēmuma vai amatpersonas pienākumu uzskaitījumu, kaut
gan citā kontekstā vārdus ražošanas funkcijas tā varētu saprast.
_________________
1 Agricultural Production Functions. Earl O. Heady, John L.
Dillon. - Jowa, 1961. Tulk.:
".Ytlb> L.Lbkkjy.
Ghjbpdjlcndtyyst aeyrwbb d ctkmcrjv [jpzbcndt.-V.% 1965. - 600 c.
2 Rhfcnbym J. Fuhj'rjyjvbxtcrbt
aeyrwbb. Hbuf% KUE> 1971. - 238 c.
3 Enciklopediskā vārdnīca. 2. sējums. - R.: Latv. enciklop.
red., 1991. - 129.lpp.
4 Enciklopēdiskā vārdnīca, 2. sēj., 3. lpp.; 1. sēj., 166.
lpp.
2. Rezultatīvai
pazīmei ražošanas funkcijā ir jābūt tādai,
kas izsaka ražotās produkcijas
daudzumu naturālā vai vērtības izteiksmē vai ražošanas intensitātes līmeni. Vispārekonomiskā līmenī tas varētu būt bruto vai preču
produkcijas daudzums absolūti vai uz 1 strādājošo, uz investēto kapitāla
vienību u.c. Tehnoloģiskā līmenī - atsevišķu izstrādājumu daudzums vai
ražošanas intensitāte, piemēram, lauksaimniecībā: graudaugu ražība, govju
vidējais izslaukums, cūku dzīvsvara diennakts pieaugums u.c.
Ja rezultatīvā pazīme izsaka kādu citu svarīgu ekonomikas
kategoriju (rādītāju), sakarību modeli parasti sauc šīs kategorijas vārdā. Tā
var runāt par pašizmaksas, ienākuma, peļņas, piedāvājuma un pieprasījuma,
uzkrājumu, labklājības, izvēles u.c. funkcijām.
Visus iepriekš minētos un citus sakarību modeļus
(funkcijas) varētu apvienot kopējā grupā ekonomikas (tautsaimniecības)
funkcijas.
Pagaidām šāds termins maz ieviesies. Ja tādu modeļu grupu
pieņemtu, varētu runāt par modeļu grupējumu pa nozarēm, piemēram,
agroekonomiskās funkcijas, dzīves līmeņa funkcijas u.t.t.
3. Modeli raksturojošiem sakarību ciešuma rādītājiem ir jābūt
samērā augstiem, lai korelatīvās sakarības
vairāk vai mazāk tuvotos funkcionālām, kaut gan funkcionālas tās nekad nebūs.
Ja sakarību ciešuma rādītāji ir zemi, virkne modeļa matemātisko pārveidojumu,
ko iesaka ražošanas funkciju teorija, kļūst maz pamatota. Līdz ar to ražošanas
funkcijā ir jābūt iekļautiem visiem svarīgākajiem ražošanas faktoriem.
Nebūs īsti pamatoti saukt par ražošanas funkciju jebkuru
regresijas vienādojumu, kurš izsaka (modelē) sakarības starp diviem vai
vairākiem ražošanu raksturojošiem rādītājiem. Lai regresijas vienādojumu varētu
saukt par ražošanas funkciju, tā uzbūvei ir jābūt profesionāli labi pamatotai
un sakarību ciešuma rādītājiem - augstiem.
4. Sakarību
formai parasti ir jābūt nelineārai. Var runāt
arī par lineārām ražošanas funkcijām, un zinātniskajā literatūrā to dara. Tomēr
tādā gadījumā modeļa interpretācija un lietošana ir tik skaidra un vienkārša,
ka nav vajadzības izmantot ražošanas funkciju teorijā izstrādātos
pārveidojumus. No otras puses, lineāra modeļa
gadījumā daži minētie pārveidojumi zaudē praktisku ekonomisku jēgu. Savukārt, lai modelī atklātos
statistiski nozīmīga sakarību nelinearitāte, faktorālo pazīmju variācijas
apgabaliem (amplitūdām) ir jābūt samērā plašiem un ir jāizmanto lieli empīriskās
informācijas masīvi.
Kā jau bijas minēts, ražošanas funkcijas, precīzāk - to
parametrus aprēķina jeb identificē, izmantojot matemātiskās statistikas, galvenokārt daudzdimensiju
statistiskas metodes. Retāk lieto kādus speciāli izstrādātus paņēmienus.
Ražošanas funkciju teorijā ir izstrādāta virkne metožu un
paņēmienu, ar kuru palīdzību pārveido,
analizē un pētī jau gatavas, aprēķinātas ražošanas funkcijas. Šīs metodes nav matemātiskās statistikas daļa, bet veido
robežzinātni starp ekonomikas teoriju, matemātisko statistiku un vispārējo
matemātiku. Tieši tādas metodes ir ekonometrijai visraksturīgākās.
13.1.3.
Ražošanas funkcijas un tās vienkāršāko pārveidojumu
grafiska
ilustrācija
Ražošanas apjoms un intensitāte parasti ir atkarīgi no
vairākiem pamatfaktoriem. Metožu demonstrācijai turpretī izvēlās tikai divu
faktoru un vienas rezultatīvās pazīmes modeli. To ar zināmām grūtībām var
attēlot trīs dimensiju telpā un viņa projekciju - plaknē.
13.1. attēlā ir parādīta divu faktoru nelineāras ražošanas
funkcijas virsma. Ar x un z ir apzīmēti
ražošanas faktori, bet ar y - ražošanas rezultāts 5. Lai attēlā parādītu virsmu, kuras punktu koordinātām,
pieaugot x un (vai) z vērtībām, pieaug y vērtības, ir izvēlēta ģeometrijā
neparasta x ass projekcija. Tādēļ citi autori ir meklējuši alternatīvu
attēla izgatavošanas paņēmienu, skat. 13.2. attēlu 6.
_________________
5 Attēls reproducēts no grāmatas: ".Ytlb> L.Lbkkjy.
Ghjbpdjlcndtyyst aeyrwbb ... c. 37.
6 Attēls reproducēts no grāmatas: Ntht[jd K.K. Ghjbpdjlcndtyyst
aeyrwbb> V.> 1974. - c. 18.
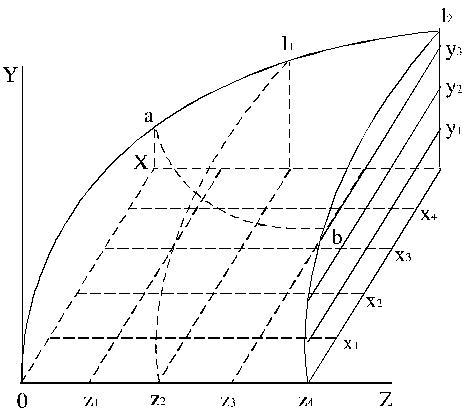
13.1. attēls. Ražošanas funkcijas virsma.
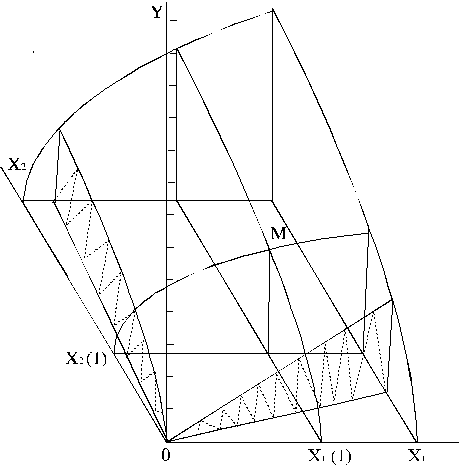
13.2. attēls. Ražošanas funkcijas virsma. Alternatīva
projekcija.
Tātad ražošanas funkcijas
y = f (x, z) virsmas daļu attēlo virsma
![]() . Šīs virsmas punktu
koordinātas apmierina funkcijā izteiktās sakarības (13.1. attēls).
. Šīs virsmas punktu
koordinātas apmierina funkcijā izteiktās sakarības (13.1. attēls).
Punkti uz ražošanas funkcijas virsmas raksturo ražošanas
plānus, kas paredz resursu racionālu
izmantošanu. Punkti, kas atrodas zem ražošanas funkcijas virsmas, raksturo
ražošanas plānus, pēc kuriem strādājot, ražošanas faktori tiek izmantoti
neracionāli. Tādēļ par tiem nav praktiska interese. Punkti virs virsmas apzīmē
neiespējamus plānus.
Ja ražošanas funkcijas virsmu šķeļ ar vertikālu plakni, kura ir
perpendikulāra kādai no faktoru asīm, iegūst šķeluma līkni, kura raksturo ražošanas
rezultāta izmaiņas, mainoties vienam faktoram pie otra faktora nemainīga
līmeņa. 13.1. attēlā ir parādīts viens tāds šķēlums ar līkni ![]() .
.
Šķeļoša plakne ir perpendikulāra OZ asij, bet paralēla OX
asij. Tādēļ ražošanas virsmas līnija ![]() raksturo ražošanas
rezultāta y izmaiņas, mainoties faktoram x, ja faktors z ir fiksēts
līmenī
raksturo ražošanas
rezultāta y izmaiņas, mainoties faktoram x, ja faktors z ir fiksēts
līmenī ![]() .
.
Citas šķēluma līknes var atrast analogi, fiksējot faktoru z citā
līmenī, piemēram, ![]() .
.
Līdzīgi var konstruēt ražošanas funkcijas virsmas šķēlumus
ar OX asij perpendikulārām, bet OZ asij paralēlām plaknēm. Tadā gadījumā iegūsim, šķēluma līnijas, kuras raksturo
ražošanas rezultāta y izmaiņas, mainoties
faktoram z pie nemainīgām x vērtībām.
Ražošanas funkcijas virsmas šķēlumus ar vertikālām plaknēm
izsaka parciālās ražošanas funkcijas. Matemātiskās statistikas terminoloģijā, ja ražošanas
funkcija ir daudzfaktoru regresijas vienādojums, tad parciālā ražošanas
funkcija ir parciālais regresijas vienādojums.
Ražošanas funkcijas vertikālos šķēlumus var iegūt pēc
patikas daudz. Tos var attēlot atsevišķā attēlā (plaknē), tāpat kā attēlo
parciālos regresijas vienādojumus (13.3. attēls). Šo attēlu var izmantot par
nomogrammu sagaidāmā (normatīvā) ražošanas rezultāta noteikšanai, mainoties
vienam ražošanas faktoram, ja otra faktora līmenis ir nemainīgs.
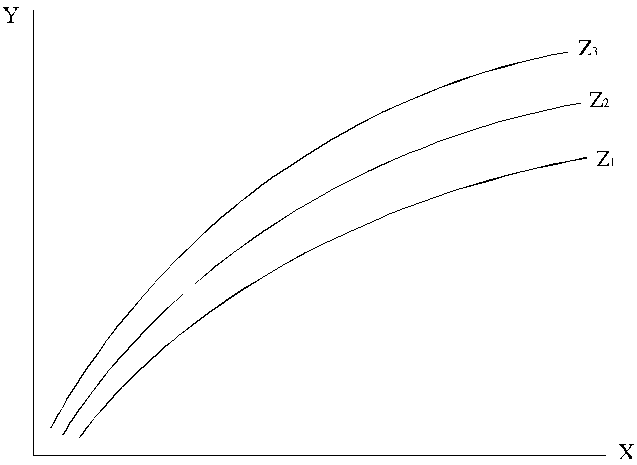
13.3. attēls. Parciālo ražošanas funkciju līknes, mainoties
faktoram x, pie trīs dažādos līmeņos fiksētiem faktora z līmeņiem.
Precīzāku sagaidāmo ražošanas rezultātu aprēķina,
ievietojot interesējošo faktora vērtību parciālajā ražošanas funkcijā, vai abu
interesējošo faktoru vērtības divu faktoru ražošanas funkcijā. Parciālās
ražošanas funkcijas atrod tāpat kā parciālās regresijas vienādojumus: sākotnējā
ražošanas funkcijā tā faktora vietā, kurš jāfiksē nemainīgā līmenī, ievieto
vajadzīgo skaitli un izdara iespējamos saīsinājumus. Ja sākotnējā ražošanas
funkcijā ir vairāk nekā divi faktori, parasti nemainīgā līmenī fiksē visus,
atskaitot vienu - interesējošo. Retāk atstāj divus mainīgos.
Kā mainās pētāmā faktora atdeve, mainoties tā nodrošinājuma
(patēriņa) līmenim, skaitliski parāda parciālas ražošanas funkcijas pirmā
atvasinātā. To sauc par papildus
rezultāta funkciju 7.
Parciālo ražošanas funkciju līkņu pieskaru tangensi rāda
papildus ražošanas rezultāta lielumu, ko nodrošina pētījamā faktora
palielināšana katrā līknes punktā, ja otrs faktors ir nemainīgā līmenī. Līkņu
pieskaru tangensi jānosaka, ņemot vērā abu skalu mērogus, nevis ar leņķmēru.
Ražošanas funkciju attēlojošo virsmu šķeļot ar horizontālu
plakni, iegūst līniju, kura raksturo fiksētu ražošanas rezultātu, ko var
sasniegt ar dažādām divu ražošanas
faktoru kombinācijām 8. 13.1. attēlā
viena tāda līnija ir parādīta kā
punktēta līkne ab. Šādas līnijas
ražošanas
funkciju teorijā sauca par ražošanas
izokvantām vai vienkārši par izokvantām, arī par
vienādu apjomu līknēm.
Tā kā ražošanas funkcijas virsmu ar horizontālām plaknēm var šķelt dažādos
augstumos, var iegūt neierobežoti daudz izokvantu. Katra izokvanta parāda visas
iespējamās faktoru x un z minimālo daudzumu kombinācijas viena izokvantai atbilstoša
ražošanas rezultāta sasniegšanai.
Arī izokvantas var attēlot atsevišķā attēlā divu dimensiju
koordinātu sistēmā, uz koordinātu asīm atliekot abu ražošanas faktoru skalas
(13.4.attēls).
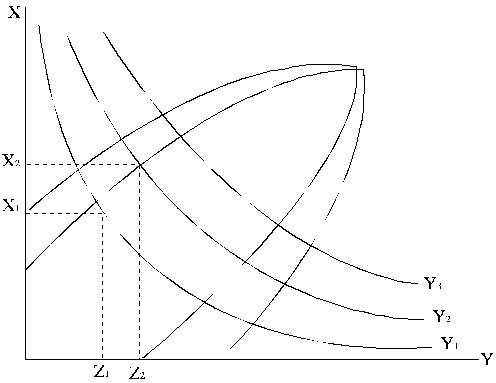
13.4. attēls. Ražošanas funkcijas izokvantas un izoklīnas.
_________________
7 Alternatīvi termini: papildus produkta funkcija,
robežrezultāta (robežprodukta) funkcija. Izvēli var
izdarīt atkarībā no konteksta.
8 Precīzāk:
izlietojot šos faktorus minimālā, nepieciešamā
līmenī. To pašu rezultātu protams, var
sasniegt arī pārtērējot vienu vai abus
faktorus. Tādas rīcības plānu izsaka visu punktu koordinātas
uz horizontālās šķelošās plaknes zem
ražošanas funkcijas virsmas. Bet tāds
ražošanas plāns nav
saprātīgs.
Līkne ![]() savieno visus punktus,
kuru koordinātām atbilstošie ražošanas faktoru līmeņi nodrošina ražošanas
rezultātu
savieno visus punktus,
kuru koordinātām atbilstošie ražošanas faktoru līmeņi nodrošina ražošanas
rezultātu ![]() . Līdzīga nozīme līknēm
. Līdzīga nozīme līknēm ![]() un
un ![]() . Šādu izokvantu kopu attēlā sauc par ražošanas virsmas kontūrkarti.
. Šādu izokvantu kopu attēlā sauc par ražošanas virsmas kontūrkarti.
Izokvantu kontūrkarti var izmantot kā nomogrammu racionālu
ražošanas faktoru līmeņu tuvinātai nolasīšanai, atbilstoši vēlamam ražošanas
rezultātam.
Izokvantas vienādojumu atrod, ievietojot ražošanas funkcijā rezultatīvās pazīmes
simbola vietā skaitli, kas atbilst noteiktam, vēlamam ražošanas rezultātam. Pēc
tam funkciju izsaka atklātā veidā pret jebkuru
no interesējošiem faktoriem. Citiem vārdiem, viena faktora lielumu
izsaka kā otra faktora funkciju.
Izokvantas pieskaru leņķa tangensi (jānosaka, ņemot vērā
abu faktoru skalas uz koordinātu asīm) raksturo attiecības, kādās viens
ražošanas faktors var samainīt otru, lai ražošanas rezultāts paliktu nemainīgs.
Ja ražošanas funkcija ir nelineāra, izokvantas arī ir
nelineāras, tātad pieskaru leņķa tangensi dažadās izokvantas daļās ir dažādi.
Tas nozīmē, ka dažādas ir arī faktoru samaināmības normas. Samainības normas vispārējā
veidā izsaka samaināmības
funkcija, kas ir izokvantas pirmā atvasinātā.
Parasti faktoru samaināmība ir pieņemamāka jeb izdevīgāka
izokvantas centrālajā daļā. Attālinoties no centrālās daļas, kad viena faktora
kļūst mazāk, to arvien grūtāk un neizdevīgāk aizstāt ar otru. Tādēļ faktoru
samaināmības normas ir nozīmīga informācija ražošanas faktoru racionālu
attiecību (samēru) noteikšanai.
Ja savieno punktus uz dažādām izokvantām, kuriem atbilst
vienādi faktoru samaināmības koeficienti, iegūst līkni, kuru sauc par izoklīnu. Tāpat
savienojot punktus, kuri atbilst citai faktoru samaināmības normai, iegūst citu
izoklīnu. Izoklīnas var atrast neierobezoti daudz.
Kad ir atrastas visizdevīgākās ražošanas faktoru
attiecības, resp., atbilstošais punkts uz izokvantas, tad no šī punkta aizejošā
izoklīna parāda, kā jāmaina vai jāsaglabā ražošanas faktoru attiecības,
paplašinot ražošanu, lai šīs attiecības joprojām būtu racionālas.
Ja izoklīnas savienojas vienā punktā (13.4. attēls),
ražošanas funkcijai ir globāls
maksimums. Tā sasniegšanai eksistē tikai viena
vienīga ražošanas faktoru līmeņu kombinācija. Manevrējot tikai ar šiem diviem
faktoriem, iegūt vēl lielāku ražošanas rezultātu vispār nevar. Tas, protams,
nenozīmē fatālu robežu, bet tikai to, ka tālākam progresam ir nepieciešams izmantot
citus ražošanas faktorus vai arī mainīt ražošanas tehnoloģiju.
Ja par ražošanas funkciju uzskata lineāru modeli, arī
izokvantas ir lineāras. Faktoru samaināmības normas visā sakarību eksistences
apgabalā ir konstantas. Pieņemot, ka tas atbilst īstenībai un ražošanas funkcija eksistē pietiekami plašā
apgabalā, racionālais variants prasītu visus pārējos ražošanas faktorus
samainīt ar vienu, kuram salīdzinoši ir vislielākā atdeve uz vienu izmaksu
vienību. Ir skaidrs, ka reāli tas nebūs iespējams, jo nodrošināt ražošanas
procesu ar vienu ražošanas faktoru nevar.
Tādēļ lineāri ražošanas modeļi sakarības var raksturot
tikai tuvināti, samērā šaurā faktoru variācijas apgabalā ar nosacījumu, ka
neviens no būtiski nepieciešamiem faktoriem pēc daudzuma nav izteikti
nepietiekams. Tāpat samēra šaurā apgabalā var izdarīt praktiskus secinājums par
faktoru samaināmību, ja šīs normas noteiktas pēc lineāra modeļa. Līdz ar to lineārs modelis kā ražošanas funkcija ir maz
efektīvs.
13.2. Rażošanas funkcijas praksč
Mācību un zinātniskā darba sākumā vieglāk un drošāk ir
iegūt modeļus, kas raksturo sakarības mikroekonomikā vai uzņēmējdarbībā.
Ieteicams sākt nevis ar ražošanas funkcijām, kur faktori un rezultāti ir
izteikti vērtības izteiksmē, bet ar tehnoloģiski ekonomiskām funkcijām, kur
visi mainīgie ir izteikti konkrētās fizikālās vienībās. Šādas sakarības ir
daudz mazāk atkarīgas no sabiedriskās iekārtas valstī, no uzņēmumu
īpašumtiesiskā veida, stingras vai liberālas saimnieciskās likumdošanas u.t.t.
Latvijā ir uzkrāta vairāku gadu desmitu pieredze, aprēķinot
ražošanas funkcijas lauksaimniecībā: ražības, izslaukuma, produkcijas
pašizmaksas u.c. funkcijas 9 .
No metodiskā viedokļa kā interesantākās varētu vērtēt
izslaukuma funkcijas. Turklāt tās ir aprēķinātas tiklab pēc trīsdesmito kā
astoņdesmito gadu datiem, kas dod iespēju izdarīt salīdzinājumus 10.
Pēc deviņdesmito gadu datiem ir iespējams aprēķināt tikai
ļoti vienkāršotas izslaukuma funkcijas.
Trīsdesmitajos gados Latvijas laukos dominēja samērā
nelielas zemnieku saimniecības kā ģimeņu privātīpašums. Astoņdesmitajos gados -
valsts un kolektīvās lielsaimniecības. Arī mājlopu turēšanas un barošanas
tehnoloģija bija atšķirīga, tomēr ne tik atškirīga, lai salīdzinājumi būtu
neiespējami.
13.2.1.
Izslaukuma funkcijas
Izslaukuma funkcijas pēc trīsdesmito gadu datiem ir
aprēķinātas par 1936/37; 1937/38; 1938/39; 1939/40. saimniecības gadiem un vidēji periodā, kā
sākotnēja informācija izmantota lopkopības pārraudzības biedrību dati. Šādu
biedrību skaits pa uzrādītajiem gadiem svarstījās no 511 līdz 901, kas ir
pietiekami daudz sakarību pētīšanai.
Izslaukuma modeļi pēc astoņdesmito gadu datiem ir
aprēķināti par katru gadu 1981. - 1986. g. periodā un šajā periodā vidēji. Kā
sākotnējā informācija izmantoti 525 - 531 lielsaimniecību gada pārskatu dati 11.
Izslaukuma funkcijas (modeļos) ir izmantoti šādi mainīgie
un to simboli.
Rezultatīvā
pazīme:
![]() - vidējais izlaukums
no vienas govs gadā, kg.
- vidējais izlaukums
no vienas govs gadā, kg.
Faktorālās
pazīmes:
![]() - barības patēriņš
(izlietojums) vidēji uz 1 govi gadā, simtos barības vienību:
- barības patēriņš
(izlietojums) vidēji uz 1 govi gadā, simtos barības vienību:
![]() - siens,
- siens,
![]() - salmi un
pelavas,
- salmi un
pelavas,
![]() - skābbarība,
- skābbarība,
![]() - lopbarības
saknes,
- lopbarības
saknes,
![]() - zaļbarība,
- zaļbarība,
![]() - spēkbarība
(koncentrētā lopbarība).
- spēkbarība
(koncentrētā lopbarība).
Ir aprēķināti gan lineāri, gan pakāpju (Koba - Duglasa)
daudzfaktoru modeļi. No metodiskā un arī praktiskā viedokļa interesantāki ir
nelineārie pakāpju modeļi. Tādēļ turpmāk runāsim par tiem. Atbilstošos lineāros
modeļus var atrast norādītajās publikācijās.
Rēķinot vidēji trīsdesmitajos gados, ir iegūts šāds modelis 12 .
_________________
9 Rhfcnbym J.G. Ghbvtytybt
htuhtccbjyyjuj fyfkbpf d bccktljdfybz[ 'rjyjvbrb ctkmcrjuj
[jpzbcndf. Hbuf> 1976. -
250 c.
Rhfcnbym J.G. Hfphf,jnrf b
bynthghtnfwbz vjltktq rjhtkfwbjyys[ cdzptq d 'rjyjvbrt.
Hbuf> 1983. - 302 c.
10 Krastiņš O., Godmane I. Barības izmantošana piena
lopkopībā: Statistiska un
ekonometriska analīze. - R.: Latvijas
Statistikas institūts, 1992. - 66 lpp.
11 Skat. 10. atsauci kā arī Krastiņš O., Godmane I.
Lopbarības izmantošana un atdeve piena
ražošanā (salīdzinoši pētījumi par 1936. -
1940 un 1981. - 1990. gadiem // Latvijas Zinātņu
Akadēmijas Vēstis. B. - 1992 - Nr. 10
(543) - 49 - 54 lpp.
12 Skat. 10. atsauci, 49. lpp.
![]() . (13.1)
. (13.1)
Visos gados statistiski nenozīmīgs izrādījās 3. faktors -
skābbarības patēriņš. Šis barības veids trīsdesmitajos gados ir nenozīmīgs
sakarā ar mazo pielietojamu tālaika lopkopībā. Salmu un pelavu devu (2.faktors)
statistiskā nozīmība pa gadiem ir atšķirīga. Lai varētu rēķināt vidējo, tā
paturēta modeli visos aprēķinos.
Izmantojot astoņdesmito gadu vidējos, ir izrēķināts šāds
analogs modelis 13:
![]() . (13.2)
. (13.2)
Pakāpju modeļiem ir šādas īpašības.
Ja kāda faktora lielumu pieņem vienādu ar nulli, tad arī
rezultatīva pazīme ir nulle. Bez jebkura svarīga ražošanas faktora ražošana nav
iespējama.
Pakāpju rādītāji ir interpretējami kā teorētiskie elastības
koeficienti, par ko plašāk jārunā atsevišķi. Īsi sakot, elastības koeficients
rāda, par cik promilēm papildus pieaug (palielinās) rezultatīvā pazīme ja faktoralā pazīme
palielinās par vienu promili.
13.2.2.
Parciālās ražošanas funkcijas
Lai labāk uztvertu ražošanas funkcijas īpatnības, visur,
kur tas iespējams, jācenšas izmantot grafiskos attēlus.
Iepriekš raksturotās daudzfaktoru izslaukuma funkcijas
tieši attēlot nevar. Lai to izdarītu, viņas ir jāvienkāršo, aplūkojot katru
faktoru atsevišķi, vai, maksimums, ne vairāk kā divus faktorus kopā.
Viena faktora ietekmi uz rezultatīvo pazīmi atspoguļo
parciālā ražošanas funkcija. To iegūst no daudzfaktoru funkcijas visus pārējos
faktorus, atskaitot vienu interesējošo, fiksējot kādā nemainīgā līmenī. Parasti
izmanto faktoru vidējās vērtības, bet, ja analīzes apsvērumi to prasa, var
izvēlēties arī jebkuras citas vērtības, piemēram, faktoru variācijas apgabalu
robežas.
Turpmāk izmantosim vidējos lielumus. Visu mainīgo lielumu
aritmētiskie vidējie 1936. - 1940. g. periodā ir šādi:
![]()
![]()
Aprēķināsim, piemēram, parciālo izslaukuma funkciju
spēkbarībai. Šim nolūkam daudzfaktoru funkcijā (1) ir jāievieto uzrādītie
vidējie lielumi, atskaitot ![]() un
un ![]() :
:
![]()
![]() .
.
![]() (13.3)
(13.3)
Šīs funkcijas grafiks 13.5. attēlā ir līkne 13.3. Līkni
uzzīmē ar vispārējo paņēmienu. Atrod vairākus punktus uz šīs līknes, dodot pēc
kārtas ![]() brīvi izvēlētas
vērtības un aprēķinot pēc parciālās funkcijas
brīvi izvēlētas
vērtības un aprēķinot pēc parciālās funkcijas![]() .
.
_________________
13 Skat. avotu 10. atsaucē, tā 50.lpp.
Kad šie punkti iezīmēti attēlā, caur tiem novelk līkni.
Piena lopkopībā par bāzes barību parasti uzlūko rupjo
barību (sienu, zaļbarību), bet par papildus barību, ar kuras palīdzību kāpināt
izslaukumu, uzlūko spēkbarību un lopbarības saknes. Tādēļ ir interesanti
aprēķināt, kāda būtu parciālā izslaukuma funkcija, ja sakņu devas fiksētu nevis
vidējās, bet minimālā un maksimālā līmenī, izejot no faktiskā šo devu
variācijas apgabala, kādas bija lietotas tālaika saimniecībās.
Pieņemam, ka minimālā sakņu deva ir 1,0 un maksimālā 6,0
(simti barības vienību jeb centneri barības vienību uz 1 govi gadā). Tad visu
citu mainīgo vietā pilnajā izslaukuma
funkcijā ievietojam faktoru vidējās vērtības, bet ![]() vietā pēc kārtas
liekam 1,0 un 4,0.
vietā pēc kārtas
liekam 1,0 un 4,0.
Iegūstam
![]() (13.4)
(13.4)
![]() (skat.13.3)
(skat.13.3)
![]() (13.5)
(13.5)
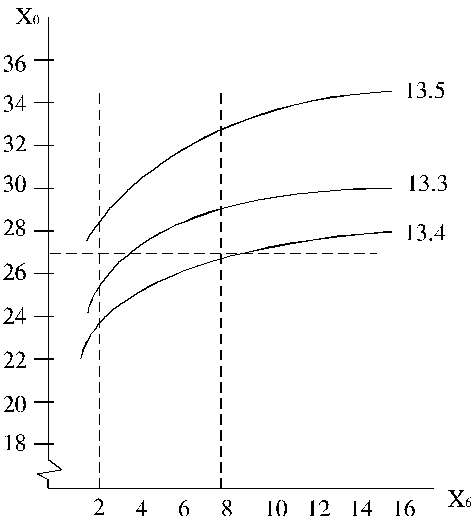
13.5. attēls. Parciālās ražošanas funkciju līknes.
Visas šīs līknes ir iezīmētas 13.5. attēlā un ļauj spriest,
kā sagaidāmas izslaukuma izmaiņas, mainot tikai spēkbarības devas (parāda
atsevišķa līkne), un mainot arī sakņu devas (pārējot no vienas līknes uz otru).
Zinot šīs līknes, kā arī lopbarības pašizmaksu vai
iepirkšanas cenu un piena pārdošanas cenu, var vērtēt, ciktāl izdevīgi
intensificēt ražošanu. Reālie aprēķini būs sarežģītāki, jo jāņem vērā nevien
barības līdzekļu patēriņa pieaugums un to atdeves samazināšanās, bet arī darba
patēriņš, amortizācija, vispārsaimnieciskie izdevumi u.c. Pēdējie,
intensificējot ražošanu, nepieaug tik strauji kā produkcijas apjomos. Tomēr,
izdarot šādus kompleksākus aprēķinus,
razošanas funkcijas, ja arī tās neietver pilnīgi visus ražošanas faktorus, dod
ļoti nozīmīgu informāciju racionālu lēmumu pieņemšanai.
Ja elastības koeficients ir mazāks par vienu, palielinot šī
faktora lielumu, tā ietekme uz rezultatīvo pazīmi (atdeve) samazinās. To sauc
par piesātinājuma efektu, un tas labi atbilst profesionāliem apsvērumiem. Ja
elastības koeficients ir lielāks par vienu ražošanas rezultāta papildus
pieaugums apsteidz faktora pieagumu. Praksē ražošanas funkcijās tas gadās ļoti
reti.
Modeļu reizinātājam jeb multiplikātoram vienkāršas
profesionālas interpretācijas nav.
Pievēršoties abu modeļu salīdzinājumiem, var atzīmēt šādas
īpatnības.
Astoņdesmito gadu modelī ir daudz lielāks spēkbarības
patēriņa ![]() elastības koeficients
nekā trīsdesmitajos gados (0,2707 pret 0,0887). To izskaidro astoņdesmito gadu
lopkopības īpatnība, kas orientējās uz plašu ievestās spēkbarības izmantošanu.
Trīsdesmitajos gados tāpat kā mūsdienās šādas iespējas nebija.
elastības koeficients
nekā trīsdesmitajos gados (0,2707 pret 0,0887). To izskaidro astoņdesmito gadu
lopkopības īpatnība, kas orientējās uz plašu ievestās spēkbarības izmantošanu.
Trīsdesmitajos gados tāpat kā mūsdienās šādas iespējas nebija.
Teorētiskie elastības koeficienti atspoguļo nevien faktora
atdevi, bet arī tā īpatsvaru rezultatīvās pazīmes veidošanā, uzdevumā - kopējā
barības devā. Tas ir tādēļ, ka galvenajiem ražošanas faktoriem ir lielāka 1
masa.
Trīsdesmitajos gados ievērojami lielāks ir zaļbarības ![]() elastības koeficients,
ko tāpat var izskaidrot ar lopkopības īpatnībām: toreiz piena ražošanai daudz
vairāk izmantoja vasaras ganību periodu,
pieļaujot lielāku ražošanas sezonalitāti.
elastības koeficients,
ko tāpat var izskaidrot ar lopkopības īpatnībām: toreiz piena ražošanai daudz
vairāk izmantoja vasaras ganību periodu,
pieļaujot lielāku ražošanas sezonalitāti.
Salmu un pelavu patēriņa ![]() elastības koeficienti
abos periodos ir negatīvi. Tas nenozīmē,
ka šīs lopbarības ietekme uz izslaukumu būtu kaitīga. Salmi un pelavas kā
mazvērtīga lopbarība tiek izmantota vienīgi tad, ja vērtīgākas barības trūkst.
Tieši vērtīgākās barības trūkums pazemina izslaukumu, kas formāli atspoguļojas
salmu un pelavu negatīvas ietekmes rādītājos. Salmu patēriņš ir sekundārs
faktors, kas īstenībā atspoguļo cita primārā faktora - lopbarības trūkuma -
ietekmi uz izslaukumu.
elastības koeficienti
abos periodos ir negatīvi. Tas nenozīmē,
ka šīs lopbarības ietekme uz izslaukumu būtu kaitīga. Salmi un pelavas kā
mazvērtīga lopbarība tiek izmantota vienīgi tad, ja vērtīgākas barības trūkst.
Tieši vērtīgākās barības trūkums pazemina izslaukumu, kas formāli atspoguļojas
salmu un pelavu negatīvas ietekmes rādītājos. Salmu patēriņš ir sekundārs
faktors, kas īstenībā atspoguļo cita primārā faktora - lopbarības trūkuma -
ietekmi uz izslaukumu.
Abos periodos ir samērā augsts lopbarības sakņu elastības koeficients. Šis barības veids abos
periodos veido salīdzināmu īpatsvaru
kopējā barības devā, un tā ietekme uz izslaukumu ir relatīvi augsta.
Detalizētāks modeļu izvērtējums mūsu metodiskā darbā nav
vajadzīgs. To var atrast iepriekš minētajos zinātniskajos darbos.
Kurš no modeļiem labāk atspoguļos ražošanas sakarības
deviņdesmito gadu apstākļos, viennozīmīgi nevar pateikt. Skaidrs, ka ievestās
spēkbarības barošanas tips Latvijai nebūs iespējams. Tuvāks varētu būt
trīsdesmito gadu modelis, tomēr tik ekstensīva ražošana kā toreiz mūsdienu
tirgus ekonomikai arī nebūs īsti piemērota.
Ja mums vajadzētu dot kādu šodienai piemērota modeļa
vērtējumu, visreālāk būtu orientēties uz abu periodu vidējo.
Turpmāk metožu demonstrācijai izmantosim trīsdesmito gadu
modeli. (13.1).
13.3.
Ražošanas funkciju matemātiski pārveidojumi
13.3.1.
Papildus rezultāta funkcija
Ja esam aprēķinājuši viena faktora
pakāpes ražošanas funkciju 14
![]() (13.6)
(13.6)
vai arī
šādas formas parciālo ražošanas funkciju, tad papildus rezultāta funkciju var
aprēķināt kā iepriekšējās funkcijas pirmo atvasināto un pierakstīt vispārējā
veidā:
![]() . (13.7)
. (13.7)
Šo izteiksmi
var izmantot tiešai konkrētās ražošanas funkcijas parametru ievietošanai.
Analogus
rezultātus dod parciālā atvasinātā no pilnās ražošanas funkcijas.
Piemēram, ja
mums ir dota divu faktoru ražošanas funkcija
![]() (13.8)
(13.8)
tad
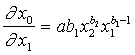 un
un 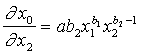 . (13.9
un 13.10)
. (13.9
un 13.10)
Atliek izteiksmē (13.9) fiksēt nemainīgā līmenī ![]() un izteiksmē (13.10)
un izteiksmē (13.10) ![]() , lai iegūtu to pašu rezultātu, ko atvasinot viena faktora
parciālo ražošanas funkciju.
, lai iegūtu to pašu rezultātu, ko atvasinot viena faktora
parciālo ražošanas funkciju.
Piemēram, izmantojot pilno ražošanas funkciju (13.1) un
fiksējot vidējā līmenī visus faktorus, atskaitot ![]() , iegūstam
, iegūstam
![]() . (skat. 13.3)
. (skat. 13.3)
Tās pirmā
atvasinātā
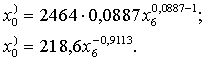 (13.11)
(13.11)
Vēlreiz izmantojot pilno ražošanas funkciju (13.1) un
fiksējot vidējā līmenī visus faktorus, atskaitot ![]() un
un ![]() , iegūstam divu faktoru izslaukuma funkciju
, iegūstam divu faktoru izslaukuma funkciju
![]() . (13.12)
. (13.12)
_________________
14 Lai
nesarežģītu turpmākos pierakstus, vilnīti uz rezultatīvās pazīmes simbola
neliksim.
Atvasinot
pēc ![]() , iegūstam
, iegūstam
 .
.
Pieņemot
tālāk ![]() vidējā līmenī
vidējā līmenī ![]() , iegūstam:
, iegūstam:
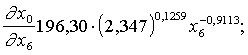
 , (skat.
13.11)
, (skat.
13.11)
kas saskan ar iepriekš aprēķināto.
Varam
izdarīt dažus secinājumus.
Ražošanas funkcijas pirmā atvasinātā ir papildus rezultāta
funkcija un izsaka papildus rezultāta lielumu katrā līknes punktā, ja faktorālo
pazīmi palielina par vienu vienību. Šai vienībai ir jābūt ļoti mazai, teorētiski - bezgalīgi mazai.
Tā kā lineāra modeļa y
= a + bx pirmā atvasinātā ![]() , tad papildus rezultāta funkcija ir interpretējama tieši
tāpat kā lineāra modeļa koeficients. Starpība tikai tā, ka lineāru sakarību gadījumā
papildus rezultāts visā sakarību eksistences apgabalā ir konstants, bet
nelineāru sakarību gadījumā - mainīgs.
, tad papildus rezultāta funkcija ir interpretējama tieši
tāpat kā lineāra modeļa koeficients. Starpība tikai tā, ka lineāru sakarību gadījumā
papildus rezultāts visā sakarību eksistences apgabalā ir konstants, bet
nelineāru sakarību gadījumā - mainīgs.
Atvasināto funkciju var aprēķināt prakstiski visām sakarību
modeļa formām, kādas lieto ekonometrijā. Tādēļ, visos gadījumos var iegūt
informāciju, kura ir līdzvērtīga tai, ko dod lineāras regresijas koeficienti.
Nelineāru modeļu parametri tiešā veidā ir profesionāli
interpretējami tikai dažos gadījumos: pakāpes modeļa pakāpes rādītāji ir
teorētiskie elastības koeficienti, zināma interpretācija ir hiperbolas
parametriem, interpretāciju nevar uzradīt parabalos u.c. modeļu parametriem. To
vietā praktiska interpretācija jāmeklē šo modeļu pārveidojumiem, piemēram,
papildus rezultāta funkcijai.
13.3.2.
Vidējais un papildus rezultāts
Vidējie lielumi ir ekonomikā visplašāk lietotie rādītāji.
Rēķina vidējos par visu interesējošo novērojumu kopu, pa atsevišķām grupām un
arī atsevišķām vienībām - uzņēmumiem.
Vidējais
ražošanas rezultāts ir speciāls vidējo lielumu
veids. To aprēķina kā intensitātes relatīvo lielumu, dalot ražošanos rezultātu
ar patērētā faktora daudzumu.
Piemēra ietvaros vidējais rezultāts būs vidējais iegūtā
piena daudzums, rēķinot uz vienu centneru patērēto spēkbarības vienību.
To var aprēķināt kā intensitātes relatīvo lielumu, dalot
saražotā piena daudzumu ![]() ar patērētās
spēkbarības daudzumu
ar patērētās
spēkbarības daudzumu ![]() . Ja abas summas aprēķinātas pēc vienu un to pašu saimniecību
datiem, vai izmantojot vienu un to pašu svaru sistēmu, tad
. Ja abas summas aprēķinātas pēc vienu un to pašu saimniecību
datiem, vai izmantojot vienu un to pašu svaru sistēmu, tad
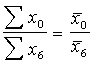 (13.13)
(13.13)
Piemērā ![]() , bet
, bet ![]() .
.
Līdz ar to, rēķinot uz 1 c barības vienību ir ražots:
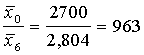 (kg piena).
(kg piena).
Šādu
rādītāju var aprēķināt arī saimniecību grupām, atsevišķai saimniecībai u.t.t.
Tā, vidējo rezultātu aprēķina, izmantojot faktiskos datus,
faktisko rezultatīvās un faktorālās pazīmes lielumus. Vispārējā gadījumā
vidējais rezultāts ir attiecība
![]() jeb
jeb ![]() . (13.14)
. (13.14)
Citos uzdevumus vidējais rezultāts būs vidējais darba
ražīgums, vidējā peļņa, rēķinot uz vienu ieguldītā kapitāla vienību u.t.t.
Ja mums ir izrēķināta ražošanas funkcija, tad rezultatīvās
pazīmes lielumu varam ņemt ne tikai kā faktiski novēroto skaitli, bet arī kā
aprēķināto jeb teorētisko lielumu, kas atbilst faktiski izlietotajam faktora
daudzumam.
Tad iepriekšējā attiecībā y aizstājam ar ![]() , resp. vidējo rezultātu izsakām ar attiecību
, resp. vidējo rezultātu izsakām ar attiecību
![]() jeb
jeb ![]() . (13.15)
. (13.15)
Piemēram, pēc iepriekšējā uzdevuma datiem gribam aprēķināt
spēkbarības izbarošanas vidējo rezultātu
![]() .
.
Ievietojot ![]() , resp.,
, resp., ![]() vietā konkrētā,
izmantotā modeļa labo pusi, iegūstam formulu vidējā rezultāta aprēķināšanai. Piemēram, ja mums ir izmantots pakāpes
modelis
vietā konkrētā,
izmantotā modeļa labo pusi, iegūstam formulu vidējā rezultāta aprēķināšanai. Piemēram, ja mums ir izmantots pakāpes
modelis ![]() , tad
, tad
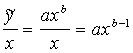 .
(13.16)
.
(13.16)
Parciālā
izslaukuma funkcija spēkbarībai bija
![]() . (skat. 13.3)
. (skat. 13.3)
No tā seko,
ka vidējais rezultāts ir
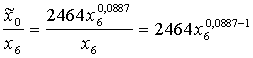 ;
;
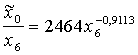 . (13.17)
. (13.17)
Pieņemot ![]() vidējā līmenī, t.i.
vidējā līmenī, t.i. ![]() , iegūstam
, iegūstam
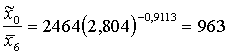
(kg piena rēķinot uz 1 c
spēkbarības barības vienību).
Skaitlis sakrīt ar iepriekš pēc vidējiem faktiskajiem
datiem aprēķināto. Modeļa līkne iet caur punktu korelācijas diagrammā, kas
atbilst abu saistīto pazīmju vidējiem.
Vispār gan šis apgalvojums ir pilnīgi pareizs tikai tad, ja
modelis ir lineārs. Ja modelis ir nelineārs, t.sk. pakāpju modelis, šāds
apgalvojums izpildās tikai tuvināti.
Aprēķināsim vidējā rezultāta (izslaukuma) lielumu dažādām ![]() (spēkbarības patēriņa)
vērtībām pēc formulas
(spēkbarības patēriņa)
vērtībām pēc formulas
 . (skat.
13.17)
. (skat.
13.17)
13.1.
tabula
Spēkbarības
vidējais un papildus rezultāts
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
10 |
12 |
15 |
|
|
2464 |
1310 |
905 |
697 |
568 |
481 |
418 |
370 |
302 |
256 |
209 |
|
|
219 |
116 |
80 |
62 |
50 |
43 |
37 |
33 |
27 |
23 |
19 |
Redzam, ka, palielinot izlietojamā faktora daudzumu,
vidējais rezultāts, rēķinot uz vienu šī faktora vienību, samazinās. Reālā
sakarību eksistences apgabalā viena barības vienība vidēji nodrošina 8 - 3 kg
piena (800 - 300 kg no centnera barības vienību).
Izdarot šādu secinājumu, jāņem vērā, ka spēkbarība ir tikai
viens no izmantojamiem barības veidiem. Bez tam piena ražošana ir atkarīga arī
no citiem faktoriem, kas nav saistīti ar lopbarību. Rēķinot vidējo rezultātu,
spēkbarībai ir pierakstīta visu šo faktoru līdzietekme. Tādēļ vidējais
rezultāts iznāk ļoti liels.
Vidējā rezultāta interpretācija no profesionālā viedokļa ir
drošāka, ja pētītais faktors ir vai nu vienīgais vai vismaz viens no nedaudzajiem, kas formē
ražošanas rezultātu. Makroekonomikā šādi faktori ir darbs, zeme, kapitāls.
Papildus
rezultāta lielumu, ko dod viena (ļoti maza)
izmantotā resursa vienība, rāda papildus rezultāta funkcija, kas ir ražošanas funkcijas pirmā atvasinātā :
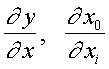 .
.
Teorētiski tā ir bezgalīgi mazu rezultatīvās un faktorālās
pazīmes pieaugumu attiecība.
Lineāra modeļa papildus rezultāta funkcija ir konstants
lielums un vienāda ar regresijas koeficientu.
Ja ir izmantots nelineārs modelis, tad papildus rezultāts
dažādām faktora vērtībām ir mainīgs (dažāds)
lielums.
Piemēram, pakāpju funkcijai
![]() ; (skat.
13.6)
; (skat.
13.6)
![]() . (skat.
13.7)
. (skat.
13.7)
Iepriekš aplūkotai parciālai izslaukuma funkcijai ![]()
papildus
rezultāta funkcija ir
![]() , (skat.
13.11)
, (skat.
13.11)
kura bija
aplūkota iepriekš.
Izrēķinām papildus rezultāta lielumu ![]() vidējai vērtībai
vidējai vērtībai
![]() (kg piena).
(kg piena).
Papildus rezultāta lielums citām ![]() vērtībām ir parādīts
13.1. tabulas 3.rindā.
vērtībām ir parādīts
13.1. tabulas 3.rindā.
Varam izdarīt virkni secinājumu.
1. Parasti parciālā ražošanas funkcijā pētāmais faktors nav
vienīgais, kas nosaka ražošanas rezultātu. Tādā gadījumā modelī ir lielāks vai
mazāks brīvais loceklis vai multiplikātors. Ja turklāt faktoram piemīt
piesātinājuma efekts, tad papildus rezultāts vienmēr būs mazāks nekā vidējais
rezutāts. Ja ir izmantots pakāpes modelis, tad, jo lielāks ir multiplikātors,
jo lielāka ir vidējā un papildus rezultātu atšķirība.
2. Papildus rezultātu un vidējo rezultātu vienmēr saista
matemātiska sakarība. Pakāpju modeļa gadījumā:
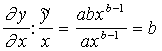 .
(13.18)
.
(13.18)
Pakāpes modeļa papildus rezultāta vērtība ir b
reizes lielāka nekā vidējā rezultāta vērtība, kur b - attiecīgā faktora pakāpes rādītājs. Tā kā pakāpes rādītājs
gandrīz vienmēr ir skaitlis mazāks par vienu: 0<b<1, tad papildus rezultāts ir mazāks par vidējo
rezultātu.
3. Tā kā papildus rezultāta funkcijā pakāpes rādītājs b - 1 parasti iznāk negatīvs skaitlis, šai funkcijai piemīt
hiperbolas īpašības. Augot x
vērtībām, samazinās papildus rezultāta vērtības, asimptotiski tuvojoties
nullei. Praktiski tas notiek tālu aiz profesionāli interpretējamās ražošanas
funkcijas eksistences apgabala.
![]()
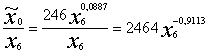 ;
;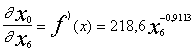 .
.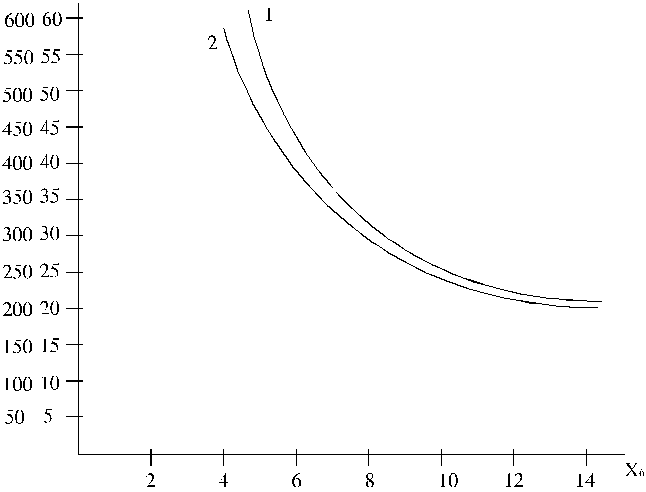
13.6. attēls. Vidējā rezultāta un papildus rezultāta
funkcijas.
Vidējā un papildus izslaukuma līknes ir parādītas 13.6.
attēlā. Jāievēro, ka papildus izslaukuma līknei ordinātu skala ir gradēta 10
reizes sīkākās vienībās nekā vidējā izslaukuma skala. Ja abas līknes iezīmē
attēlā ar vienādi iedalītu ordinātu skalu, tās atrodas tālu viena no otras.
13.3.3.
Izokvantas
Ražošanas faktori parasti zināmās robežās ir savstarpēji
samaināmi. Uzskatāmi tas redzams izslaukuma funkcijā, kur runa ir par viena
barības līdzekļa aizstāšanu ar otru. Saprotams, ka šāda samaināmība ir
ierobežota un kļūst neizdevīga tad, ja aizstāšanas rezultātā kāda no faktoriem kļūst maz.
Lai izpētītu ražošanas faktoru samaināmību ar
ekonometriskām metodēm, aprēķina un novērtē ražošanas funkcijas izokvantas.
Lai pētītu divu faktoru savstarpējo samaināmību ar
nosacījumu, ka pārējie faktori fiksēti nemainīgā līmenī, visvienkāršāk
aprēķināt divu faktoru parciālo ražošanas funkciju un pēc tam - tās izokvantas.
Divu faktoru parciālo izslaukuma funkciju (sakņu un
spēkbarības devām) aprēķina līdzīgi kā
viena faktora parciālo izslaukuma funkciju. Tikai - kā mainīgus
lielumus, nefiksējot noteiktā līmenī, saglabā divus faktorus, piemērā, ![]() un
un ![]() .
.
Izdarot ievietojumus, iegūstam, ka ![]() (skat. 13.12)
(skat. 13.12)
Jāievēro, ka visās parciālās ražošanas funkcijās, kas
aprēķinātas no vienas pamatfunkcijas, atbilstošie elastības koeficienti sagalabājas
vieni un tie paši. Pārējo faktoru fiksēšanas rezultātā mainās vienīgi modeļa
reizinātājs - multiplikātors.
Lai aprēķinātu pēdējās izslaukuma funkcijas izokvantas,
ražošanas apjoms (izslaukums ![]() ) ir jāpieņem kādā brīvi izvēlētā līmenī un izteiksme
jāpārveido atklātā veidā pret vienu no faktoriem -
) ir jāpieņem kādā brīvi izvēlētā līmenī un izteiksme
jāpārveido atklātā veidā pret vienu no faktoriem - ![]() vai
vai ![]() .
.
Iepriekšējai funkcijai
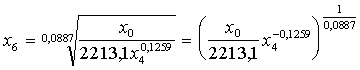 . (13.19)
. (13.19)
Pieņemot,
piemēram, ka ![]() (kg), šo izteiksmi var
vienkāršot līdz
(kg), šo izteiksmi var
vienkāršot līdz
![]() . (13.20)
. (13.20)
Tā ir konkrēta izokvantas funkcija, kurai 13.7. attēlā
atbilst 2.līkne. Līknes punktu koordinātas var izskaitļot, dodot brīvi izvēlētas vērtības šī faktora variācijas apgabalā un aprēķinot ![]() . Piemēram, ja
. Piemēram, ja ![]() , tad
, tad ![]() .
.
Izokvantas citiem brīvi fiksētiem izslaukuma līmeņiem
ir parādītas 13.7. attēlā.
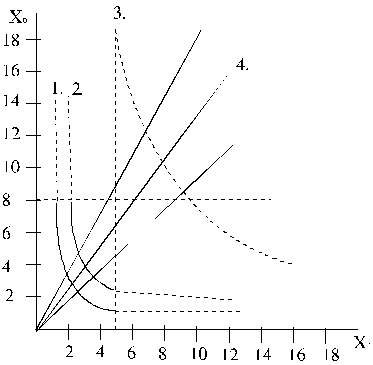
13.7. attēls. Izokvantas un izoklīnas.
Katrs punkts uz izvēlētās izokvantas atspoguļo vienu
ražošanas plānu (barības līdzekļu kombināciju), kas nodrošina vēlamo rezultātu
(izslaukumu). Saprotams, ka daži no šiem plāniem ir izdevīgāki, citi mazāk
izdevīgi. Viens no viņiem ir optimāls, ņemot vērā salīdzināmo barības līdzekļu
100 barības vienību pašizmaksu vai
iepirkšanas cenu. Faktisko datu variācijas apgabalā līknes zīmētas
nepārtrauktas, ekstrapolācijas apgabalā - pārtrauktas.
Izokvantas vienādojumu var izteikt vispārējā
veidā. Piemēram, ir dota ražošanas funkcija
![]() (13.21)
(13.21)
Uzskatot ![]() par konstantu lielumu,
izsakām funkciju atklātā veidā pret
par konstantu lielumu,
izsakām funkciju atklātā veidā pret ![]() :
:
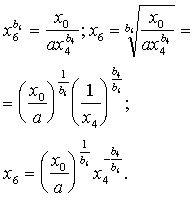 (13.22)
(13.22)
Vispārinot, ja ir
dota ražošanas funkcija
![]() , (13.23)
, (13.23)
tad
izokvantas ir šādas
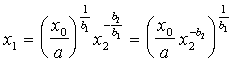 ; (13.24)
; (13.24)
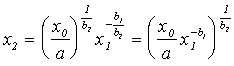 . (13.25)
. (13.25)
Ja ir jārēķina daudz punktu koordinātas uz vairākām
izokvantām, šīs formulas viegli programmēt.
Katrai izokvantai jāfiksē atmiņās ![]() un kā mainīgās jāņem
un kā mainīgās jāņem ![]() , resp.
, resp. ![]() brīvi izvēlētas vērtības.
brīvi izvēlētas vērtības.
Iepriekš risinātajā piemērā
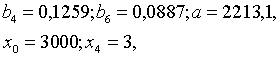
__________________
Atgādinājumi:
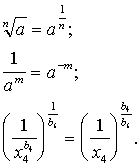
tad,
ievietojot formulā (13.22), iegūstam :
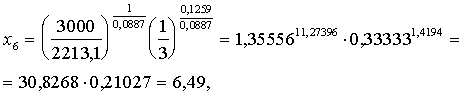
kas saskan
ar iepriekšējo.
Tātad izokvantu var aprēķināt:
1) izmantojot jau konkrētu ar
skaitliskiem parametriem dotu ražošanas funkciju un to vienkāršojot;
2) izmantojot izokvantas formulas
vispārējā veidā un tajās ievietojot ražošanas funkcijas parametrus un fiksēto
ražošanas apjomu ![]() .
.
Pēc tam var izdarīt vienkāršojumus.
13.3.4. Faktoru samaināmības funkcijas un
samaināmības normas
Faktoru
samaināmības funkcija parāda, kā iespējams vienu ražošanas faktoru samainīt ar
otru, lai ražošanas apjoms paliktu nemainīgs.
Samaināmības
funkciju atrod kā izokvantas pirmo atvasināto.
Aprēķinus
atkal var izdarīt:
1)
strādājot ar konkrētas izokvantas vienādojumu;
2)
vispārējā veidā.
1. Izpētām
izokvantu:
![]() , (skat. 13.20)
, (skat. 13.20)
kur ![]() - faktors, ar kuru gribam aizstāt (spēkbarība),
- faktors, ar kuru gribam aizstāt (spēkbarība),
![]() - faktors, kuru gribam
aizstāt (lopbarības saknes).
- faktors, kuru gribam
aizstāt (lopbarības saknes).
Rezultatīvā
pazīme ![]() fiksēta 3000 kg
līmenī.
fiksēta 3000 kg
līmenī.
Aprēķinam
izokvantas pirmo atvasināto
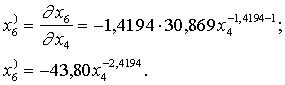 (13.26)
(13.26)
Konkrēta
pirmās atvasinātās ordināta rāda samaināmības normu interesējošā punktā.
Samaināmības funkcija ģeometriski nozīmē izokvantas
pieskaru leņku tangensus, kuri dažādos izokvantas punktos ir dažādi. (13.8.
attēls).
![]()
![]()
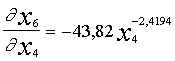 .
.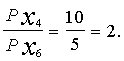
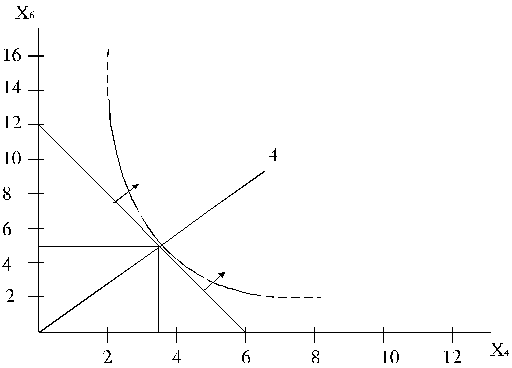
13.8. attēls.Izokvanta.
13.2. tabula
Samaināmās
normas
|
|
1 |
2 |
3 |
4 |
5 |
6 |
8 |
|
|
30,9 |
11,5 |
6,5 |
4,3 |
3,14 |
2,4 |
1,6 |
|
|
43,8 |
8,19 |
3,07 |
1,53 |
0,89 |
0,57 |
0,29 |
Aprēķinām sakņu ![]() samaināmības
normu ar spēkbarību
samaināmības
normu ar spēkbarību ![]() izokvantas punktā,
kur
izokvantas punktā,
kur ![]() (ievietojot izokvantas
vienādojumā, uzzinam, ka
(ievietojot izokvantas
vienādojumā, uzzinam, ka ![]() ) (13.2. tabula).
) (13.2. tabula).
Samaināmības normu apzīmē
ar - K, līdz ar ko ![]() , kurā jāievieto
, kurā jāievieto ![]() iegūstam, ka
iegūstam, ka ![]() (13.2. tabula).
(13.2. tabula).
Tātad vienu
vienību ![]() (100 barības vienību
sakņu) šajā izokvantas punktā var aizstāt ar 0,89 vienībām
(100 barības vienību
sakņu) šajā izokvantas punktā var aizstāt ar 0,89 vienībām ![]() (89 vienībām
spēkbarības). Ja abu barības veidu pašizmaksa par barības vienību būtu vienāda,
aizstāšana būtu izdevīga.
(89 vienībām
spēkbarības). Ja abu barības veidu pašizmaksa par barības vienību būtu vienāda,
aizstāšana būtu izdevīga.
Savukārt,
pieņemot, ka
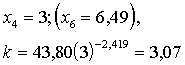 (13.2. tabulas
3.rinda)
(13.2. tabulas
3.rinda)
Lai aizstātu
100 barības vienības sakņu, ir jāizbaro 307 barības vienības spēkbarības, kas
diezin vai būs izdevīgi.
Vienmēr jāņem vērā, vai izpētītie punkti uz izokvantas
vispār ir sakarību reālās eksistences apgabalā un samainīšana vispār ir
iespējama. To nenosaka ar ekonometrijas metodēm, bet ar profesionālām zināšanām
no konkrētās nozares.
Ir redzams, ka to faktoru, kura kļūst maz, arvien
neizdevīgāk aizstāt ar otru faktoru.
Faktoru samaināmības normu var tuvināti aprēķināt, vizuāli novelkot
izokvantai interesējošā punktā pieskari, līdz tā krustojas ar koordinātu asīm.
Nolasīt šos krustpunktu koordinātas un
izdalīt vienu skaitli ar otru. Piemēram, pēc 13.8. attēla punktā ![]() izokvantas pieskare
krusto
izokvantas pieskare
krusto ![]() asi punktā 12 un
asi punktā 12 un ![]() asi - punktā 6. No tā
seko, ka
asi - punktā 6. No tā
seko, ka
![]() (aprēķinājām 3,07).
(aprēķinājām 3,07).
Šāds
novērtējums palīdz, ja rodas šaubas par
to, kā interprētēt atrasto samaināmības normu (kurš faktors ir tas, ar kuru
samainām, un kurš tas, kuru samainām).
2. Samaināmības funkciju var izteikt arī vispārējā veidā.
To var izdarīt ar diviem paņēmieniem.
2.1. Pamatpaņēmiens paredz tieši atvasināt izokvantas
funkciju. To samērā viegli izdarīt ar
pakāpes funkciju. Dažu citu sakarību formu gadījumā tas noved pie sarežģītiem
pārveidojumiem un lietderīgāks ir otrs paņēmiens.
Ja ir dota
pakāpju ražošanas funkcija
![]() , (skat.
13.8)
, (skat.
13.8)
tad tās izokvanta, kā parādīts
iepriekš, ir
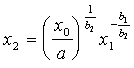 . (skat. 13.25)
. (skat. 13.25)
Atvasinam šo
funkciju pēc ![]()
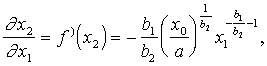 (13.27)
(13.27)
ko var
pierakstīt tālākam darbam ērtākā veidā, novietojot nemainīgo ![]() izteiksmes beigās un
atbrīvojoties no dalīšanas:
izteiksmes beigās un
atbrīvojoties no dalīšanas:
![]() . (13.28)
. (13.28)
Atrodam no
ražošanas funkcijas
![]() (skat. 13.8)
(skat. 13.8)
lielumu ![]()
![]() (13.29)
(13.29)
un ievietojam to izteiksmē (13.28)
![]() , (13.30)
, (13.30)
ko var saīsināt (vienādo reizināmo pakāpes rādītājus saskaita)
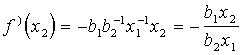 , (13.31)
, (13.31)
analogi
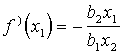 . (13.32)
. (13.32)
Piemērā
izpētījām samaināmības normu punktā
![]() .
.
Mainot faktora ![]() kodu uz
kodu uz ![]() un
un ![]() uz
uz ![]() , varam ievietot atrastajā samaināmības funkcijas formulā
, varam ievietot atrastajā samaināmības funkcijas formulā

kas sakrīt ar iepriekš aprēķināto.
2.2. Ja ražošanas funkcijas forma ir tāda, ka tās
izokvantas atvasināšana un pārveidošana rada grūtības, tad samaināmības
funkciju nosaka kā divu papildus rezultāta funkciju apgrieztu attiecību, ņemtu
ar pretēju zīmi.
Ražošanas
funkcijas
![]() (skat. 13.8)
(skat. 13.8)
papildus rezultāta funkcijas (pirmās
atvasinātās) ir
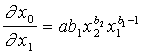 (13.33)
(13.33)
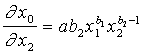 (13.34)
(13.34)
 (13.35)
(13.35)
kas sakrīt ar iepriekšējo.
13.3.5.
Faktoru attiecību optimizācija
Par ražošanas faktoru optimizāciju sauksim kādu ražošanas
faktoru samēru aprēķināšanu, izejot no viņu samaināmības normām un šo faktoru
pašizmaksas, resp., iepirkšanas cenas.
Pilna optimizācija prasa ievērot visu kompleksu ražošanas
faktoru, izdevumus sakarā ar viņu izmantošanu utt. Pilno optimizāciju ne
vienmēr iespējams izdarīt, tādēļ arī atsevišķu faktoru optimizācijai kā lokālam
uzdevumam ir praktiska nozīme.
Ja iepriekšējā uzdevuma ietvaros pieņemtu, ka 100 barības
vienības sakņu maksā aptuveni tikpat, cik 100 barības vienības spēkbarības, tad
no jau aprēķinātajām samaināmības normām un no 2. izokvantas 13.2. attēlā
jāsecina, ka izslaukuma 3000 kg no govs iegūšanai izbarojamo sakņu daudzumam ir
jābūt lielākam par 3 simtiem un mazākam par 5 simtiem barības vienību, ņemot
atbilstoši izokvantai vajadzīgo spēkbarības daudzumu, jo šajā daļā izokvanta ir
pietiekami izliekta (nepārtraukta
līnija).
Aprēķināsim, cik tieši jāņem sakņu un cik spēkbarības, ja
pieņem, ka abu barības veidu barības vienība maksā vienādi.
Tas nozīmē, ka ir jāmeklē tāds punkts uz izokvantas
![]() , (skat. 13.20)
, (skat. 13.20)
kur
pieskares leņķa tangenss ir viens. Pieskares leņķu tangensus izsaka atbilstošā
samaināmības funkcija, ko atrod kā izokvantas pirmo atvasināto
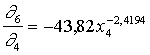 . (skat.
13.26)
. (skat.
13.26)
Pielīdzinot
šo funkciju mīnus vienam, iegūstam
![]() no kā seko, ka
no kā seko, ka
![]() (simti
b.v.).
(simti
b.v.).
Izvērstāk:
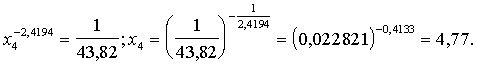
Aprēķinam šim plānam atbilstošo spēkbarības daudzumu,
ievietojot ![]() izokvantas vienādojumā
izokvantas vienādojumā
![]() (simti b.v.).
(simti b.v.).
Plāna atbilstību iecerei pārbauda, abus faktoru daudzumus
ievietojot ražošanas funkcijā:
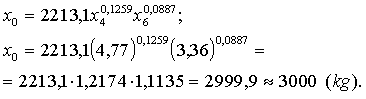
Plāns
paredzēto izslaukumu nodrošina.
Plāns paredz izbarot vairāk sakņu nekā spēkbarības, jo
sakņu atdeve no vienas barības vienības lielāka, bet pašizmaksu pieņēmām
vienādu.
Praksē dažādu faktoru, piemērā - barības līdzekļu, izmaksas
nav vienādas. Trīsdesmito gadu zemnieku saimniecībās 100 barības vienību
pašizmaksa bija: lopbarības saknēm Ls
10,- lopbarības graudiem (spēkbarībai) -
Ls 8,-. Tagad, salīdzinot ar trīsdesmitajiem gadiem, vairāk mehanizēta ir
graudu ražošana, mazāk sakņu. Tādēļ pieņemsim, ka ![]() .
.
Ar šiem nosacījumiem, ja abu barības veidu 100 barības
vienības dotu vienādu atdevi, būtu jāizbaro divas reizes vairāk spēkbarības
nekā sakņu. Tā kā abu barības veidu atdeve nav vienāda, izmaksu attiecībai
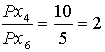
jāpielīdzina
samaināmības funkcija
![]() (skat.
13.26)
(skat.
13.26)
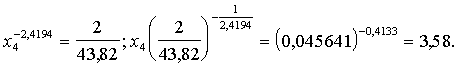
Ir jāizbaro
3,58 c.b.v. sakņu.
Vajadzīgo spēkbarības daudzumu atrod, ievietojot atrasto ![]() vērtību izokvantas
vienādojumā
vērtību izokvantas
vienādojumā
![]() (skat. 13.20)
(skat. 13.20)
![]() c.b.v. spēkbarības.
c.b.v. spēkbarības.
Tātad optimālais plāns, lai iegūtu 3000 kg lielu
izslaukumu, paredz izbarot 3,58 c.b.v.
sakņu un 5,05 c.b.v. spēkbarības.
Aprēķinu
pareizību pārbauda, ievietojot šos skaitļus ražošanas funkcijā;
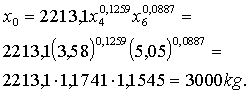
Nereti, rēķinot faktoru samaināmības normas, iznāk
kļūdīties, nepareizi ievietojot formulās faktoru, kuru samaina un uz kuru samaina.
Lai
pārbaudītu vai neesam kļūdijušies, aprēķinu pareizība jāpārbauda grafiski
(13.8. attēls).
Tā kā uzdevuma nosacījumi paredzēja, ka spēkbarība ir divas
reizes lētāka nekā saknes, uzzīmējam pašizmaksu attiecību taisni, piemēram,
ņemot uz ![]() skalas 12 un uz
skalas 12 un uz ![]() skalas 6 (divas reizes mazāk) un šos punktus savienojot ar
taisni. Pārbīdot šo taisni paralēli pašai sev izokvantas virzienā, novērtējot
punktu, kurā abas līnijas pirmo reizi saskarsies.
skalas 6 (divas reizes mazāk) un šos punktus savienojot ar
taisni. Pārbīdot šo taisni paralēli pašai sev izokvantas virzienā, novērtējot
punktu, kurā abas līnijas pirmo reizi saskarsies.
Tas notiek aptuveni punktā ar koordinātām ![]() Katrā ziņā redzam, ka
Katrā ziņā redzam, ka ![]() ir lielāks nekā
ir lielāks nekā ![]() . Tātad aprēķinātie lielumi
. Tātad aprēķinātie lielumi ![]() kļūdas dēļ nav
samainīti vietām.
kļūdas dēļ nav
samainīti vietām.
Ja grib samainīt ![]() ar
ar ![]() (otrādi), tad
izokvanta jārēķina atklātā veidā pret
(otrādi), tad
izokvanta jārēķina atklātā veidā pret ![]() un daudzumu attiecība
būs
un daudzumu attiecība
būs ![]() . Turpretī cenu attiecība, kurai pielīdzina samaināmības
funkciju, jāņem apgriesta
. Turpretī cenu attiecība, kurai pielīdzina samaināmības
funkciju, jāņem apgriesta ![]() .
.
13.3.6.
Izoklīnas
Izoklīna ir līnija, kas savieno dažādu izokvantu punktus ar
vienādām faktoru samaināmības normām.
Izoklīnas vienādojumu atrod, pielīdzinot samaināmības
funkciju izvēlētai, resp. optimizētai konstantei k. Tādējādi pakāpes funkcijai
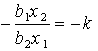 , (13.36)
, (13.36)
no kā seko, ka
 , (13.37)
, (13.37)
kas ir izokvantas vienādojums.
Aizvietojot
piemērā 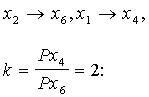
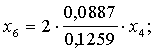
![]() . (13.38)
. (13.38)
Pārbaudām
vai punkts (3,58; 5,05), kas fiksēja optimālo faktoru attiecību uz otrās
izokvantas, atrodas uz tikko aprēķinātās izoklīnas:
![]() .
.
Tātad
atrodas, un izoklīna ir noteikta
pareizi.
Ja ražošanas funkcijai ir pakāpes funkcijas forma,
izoklīnas ir lineāras un atšķiras ar samaināmības normām k. Atbilstošās taisnes ar dažādiem faktoru samaināmības
koeficientiem vēdekļveidā iziet no koordinātu sākuma (13.7. attēls).
Ja
izpildītājs par iegūtajiem rezultātiem nav īsti drošs, kā arī tad, ja aprēķinu
rezultāti prasa lielu atbildību, ir jānovērtē naudas izteiksmē nevien atrastais
optimālais plāns, bet arī alternatīvi plāni abpus optimālajam, pārliecinoties,
ka optimālais plāns patiešām ir izdevīgāks.
13.4.
Ieņēmumu un izdevumu funkcijas
Ieņēmumu funkciju iegūstam, pareizinot rezultatīvās pazīmes
naturālām vienībām izteiktu ražošanas funkciju ar vienas rezultatīvās pazīmes
vienības cenu. Vienkāršības dēļ vēlreiz aplūkosim parciālo izslaukuma funkciju
![]() (skat. 13.3.)
(skat. 13.3.)
Pieņemsim,
ka 1 kg piena var pārdot par Ls 0,10. Tad, apzīmējot ieņēmumus no vienas govs
gadā ar V, var pierakstīt
![]() (Ls) (13.39)
(Ls) (13.39)
Šī ieņēmumu
līkne ir tabulēta 13.3. tabulas 1.-2.rindās un parādīta grafiskajā 13.9.
attēlā.
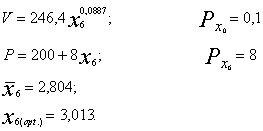
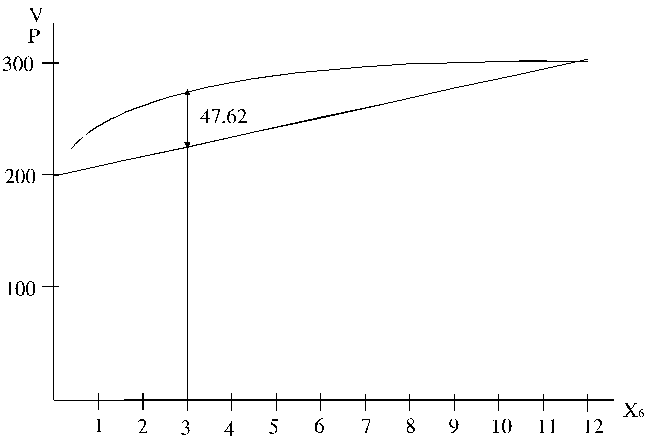
13.9. attēls. Ieņēmumu līkne un izdevumu taisne.
13.3. tabula
Ieņēmumu un izdevumu līknes
|
|
0.5 |
1 |
2 |
3 |
4 |
5 |
8 |
10 |
12 |
15 |
|
V |
232 |
246 |
262,02 |
271,62 |
279 |
284 |
296 |
302 |
307 |
313 |
|
P |
204 |
208 |
216 |
224 |
232 |
240 |
264 |
280 |
296 |
320 |
|
V - P |
28 |
38 |
46 |
48 (47,62) |
47 |
44 |
32 |
22 |
11 |
-7 |
Izdevumu funkciju konstruējam tā, ka pieņemam viena c
barības vienību spēkbarības pašizmaksu Ls 8,-, bet vienas govs pastāvīgās
turēšanas izmaksas (bez spēkbarības) Ls 200,- gadā. Tad izdevumu funkcija
būs
![]() . (13.40)
. (13.40)
Tā ir tabulēta iepriekšējās tabulas 3.rindā un parādīta arī
attēlā kā taisne.
Peļņas funkcija būs ieņēmumu un izdevumu funkciju starpība.
Tabulā - pēdējā rinda. Attēlā tā ir attālums starp līkni un taisni, mērot pa
vertikāli un nolasot attālumu ordinātu skalā.
Tabulā
redzam, un pēc attēla varam pārliecināties, ka vislielāko peļņu var iegūt,
izbarojot govīm ap 3 c barības vienību
spēkbarības gadā.
Mūsdienu apstākļiem tā ir maza deva, bet trīsdesmito gadu
zemnieku saimniecībās pat pārsniedza vidējo ![]() .
.
Mūsdienu apstākļiem tuvākas izdevumu un ienākumu funkcijas
rāda, ka visizdevīgāk izbarot ap 8 c spēkbarības, rēķinot vidēji uz 1 govi
gadā.
Optimālo
faktora daudzumu, kas maksimizē peļņu, var atrast trejādi.
1. Pielīdzinot ieņēmumu funkcijas pirmo atvasināto faktora vienas vienības
cenai ![]() :
:
![]() ;
;
![]() . (13.41)
. (13.41)
To pielīdzina skaitlim P = 8:
![]() (13.42)
(13.42)
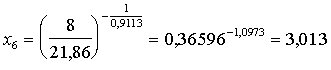
(c spēkbarības uz vienu govi).
Aprēķinātais
plāns nodrošina šādus ieņēmumus (ievietojot ieņēmumu funkcijā), izdevumus
(ievietojot izdevumu funkcijā) un peļņu (abu starpību):
Pēc optimālā
plāna: Nedaudz
novirzoties no optimālā plāna:
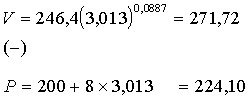
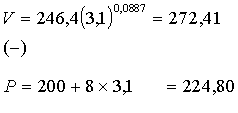
___________
____________
47,62 (Ls no govs)
47,61
(par
1 sant. mazāk)
2.
Pielīdzinot sākotnējās parciālās ražošanas funkcijas pirmo atvasināto faktora
un rezultāta vienu vienību cenu attiecībai:
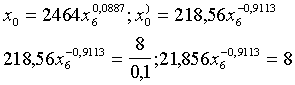 (skat. 13.11)
(skat. 13.11)
un tālāk kā iepriekš 1.punktā.
3.
Pielīdzinot nullei ienākumu un izmaksu funkciju starpības pirmo atvasināto
![]() ; (13.43)
; (13.43) ![]() ;
;
![]() . (13.44)
. (13.44)
un tālāk kā 1.punktā. Optimālais ![]() .
.
Lai pārbaudītu, vai plāns patiešām optimāls,
izdara tos pašus aprēķinus, ņemot ![]() nedaudz mazāku
nedaudz mazāku ![]() un nedaudz lielāku
un nedaudz lielāku ![]() :
:
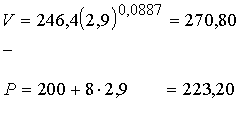
____________
47,60
(par 2 sant. mazāk)
Spēkbarības devas un tām atbilstošo izslaukumu, kas
nodrošina maksimālu peļņu, mēs noteicām, izmantojot augšup izliektu ieņēmumu
līkni un lineāru izmaksu taisni. Mikroekonomikas kursos nereti to pašu uzdevumu
ieteic risināt, izmantojot lineāru ieņēmumu taisni un lejup izliektu izmaksu
līkni 15. Tādēļ ir jānoskaidro, kā abas pieejas ir saistītas un vai
tās dod vienus un tos pašus rezultātus.
_____________
15 Stiglics Dž. E. un Drifils Dž. Ekonomika: mikroekonomika.
R.: 1995. - 287. Lpp.
Salīdzinot abas uzdevumu nostādnes un tiem atbilstošos
grafiskos attēlus, redzam, ka mēs uz horizontālās ass esam atlikuši faktora - spēkbarības
![]() skalu, bet
mikroekonomikas kursā ir atlikta rezultatīvās pazīmes skala, mūsu piemērā -
izslaukums.
skalu, bet
mikroekonomikas kursā ir atlikta rezultatīvās pazīmes skala, mūsu piemērā -
izslaukums.
Lai realizētu pēdējo nostādni, izslaukuma funkcija ![]() ir jāizsaka atklātā
veidā pret
ir jāizsaka atklātā
veidā pret ![]() . Tā parādīs, kāda spēkbarības deva ir nepieciešama, lai
varētu sagaidīt brīvi izvēlētu izslaukumu. Nosauksīm to par inverso izslaukuma
funkciju.
. Tā parādīs, kāda spēkbarības deva ir nepieciešama, lai
varētu sagaidīt brīvi izvēlētu izslaukumu. Nosauksīm to par inverso izslaukuma
funkciju.
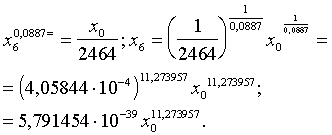 (13.45)
(13.45)
Pārsteidz, ka inversās izslaukuma funkcijas reizinātājs jeb
multiplikātors ir tik mazs skaitlis, kāds ir pierasts vienīgi kodolfizikā. Viņu kompensē otrs reizinātājs -
![]() pakāpe, kurš savukārt
pakāpe, kurš savukārt ![]() normālas variācijas
apgabalā būs ļoti liels skaitlis.
normālas variācijas
apgabalā būs ļoti liels skaitlis.
Inversā izslaukuma funkcija dažām brīvi izvēlētām ![]() vērtībām ir tabulēta
sekojošas tabulas pirmajās divās rindās.
vērtībām ir tabulēta
sekojošas tabulas pirmajās divās rindās.
13.4.
tabula
Inversa
izslaukuma izdevumu un ieņēmumu funkcijas
|
|
2300 |
2400 |
2500 |
2600 |
2717,22 |
2800 |
2900 |
3000 |
3200 |
3500 |
|
|
0,46 |
0,74 |
1,18 |
1,83 |
3,0135 |
4,23 |
6,28 |
9,20 |
19,04 |
52,29 |
|
P |
203 |
206 |
209 |
215 |
224 |
234 |
250 |
274 |
352 |
618 |
|
V |
230 |
240 |
250 |
260 |
272 |
280 |
290 |
300 |
320 |
350 |
|
V - P |
27 |
34 |
41 |
45 |
48 |
46 |
40 |
26 |
-32 |
-268 |
Redzam, ka palielinot tikai spēkbarības daudzumu, nav
iespējams kāpināt izslaukumu augstāk par apmēram 3000 kg no govs gadā. Tālākam
pieaugumam būtu nepieciešamas tik lielas spēkbarības devas, kādas govis
vienkārši nespētu apēst. Pats par sevi saprotams, ka tās būtu arī saimnieciski
neizdevīgas.
Izdevumu funkciju var atrast, pareizinot inverso izslaukuma
funkciju ar vienas vienības faktora (spēkbarības) cenu (piemērā ![]() ) un pieskaitot pastāvīgās izmaksas, piemērā 200. Vieglāk to
izdarīt, pareizinot ar 8 un pieskaitot 200
13.4. tabulas 2.rindas skaitļus; skat. tabulas 3.rindu. Šī izmaksu
līkne, kā tas pieņemts mikroekonomikā, ir izliekta līkne, kas strauji kāpj pie
lieliem produkcijas daudzumiem (labajā zarā, skat. 13.10. attēlu).
) un pieskaitot pastāvīgās izmaksas, piemērā 200. Vieglāk to
izdarīt, pareizinot ar 8 un pieskaitot 200
13.4. tabulas 2.rindas skaitļus; skat. tabulas 3.rindu. Šī izmaksu
līkne, kā tas pieņemts mikroekonomikā, ir izliekta līkne, kas strauji kāpj pie
lieliem produkcijas daudzumiem (labajā zarā, skat. 13.10. attēlu).
p - izdevumi v - ieòçmumi
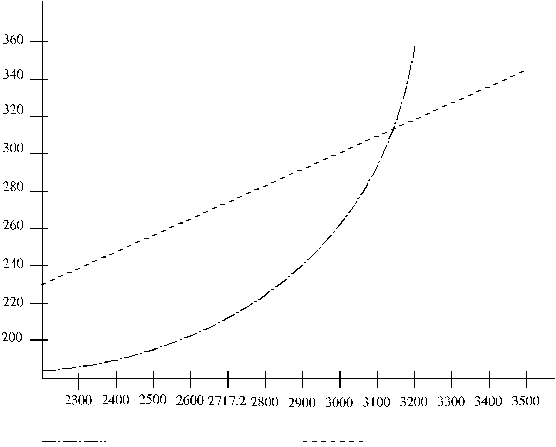
13.10. attēls. Ieņēmumu un izdevumu funkcijas, kā tās
parāda mikroekonomikā.
Ieņēmumi ir izsakāmi ar taisnes vienādojumu, vienkārši
pareizinot produkcijas apjomu ar realizācijas cenu, piemērā ![]()
![]() , (13.46)
, (13.46)
skat. 13.4.
tabulas 4.rindu. Peļņu aprēķina kā ieņēmumu un uzdevumu starpību, tabulas
pēdējā rinda. Attēlā tā ir attālums starp taisni un līkni.
Tiklab tabulā kā attēlā ir redzams, ka peļņas maksimums
piemēra ietvaros tiek sasniegts, ja izslaukums ir ap 2700 kg, ko nodrošina
spēkbarības devas ap 3 simti barības vienību, rēķinot vidēji uz govi gadā. Tas
pilnīgi atbilst iepriekšējiem aprēķiniem.
Izmantojot jauno aprēķinu variantu, precīzu optimumu var
atrast, pielīdzinot nullei peļņas funkcijas pirmo atvasināto. Peļņas funkcija
savukārt ir ieņēmumu un izdevumu funkciju starpība.
 (13.47)
(13.47)
![]() (13.48)
(13.48)
Pielīdzinot
to nullei, iegūstam

(kg)
Tātad vislielāko peļņu nodrošina izslaukums 2717 kg no govs
gadā. Kāda šim izslaukumam ir nepieciešama spēkbarības deva, to nosaka,
ievietojot 2717 inversajā izslaukuma funkcijā
![]() (c barības
vienību).
(c barības
vienību).
Optimālais plāns dod ienākumu 0,1 x 2717 = 271,70 (Ls) un prasa izdevumus
(ievietojot 3,011 izdevumu funkcijā):
![]() (Ls)
(Ls)
Optimālā peļņa V - P
= 271,70 - 224,08 = 47,62 (Ls) (Skat.
13.4. tabulas pēdējās rindas).
Rezultāti, ja neskaita iespējamās noapaļošanas kļūdas, ar
abiem paņēmieniem ir iegūti vienādi, tikai pēdējā gadījumā vajadzēja darboties
ar atomāri maziem un astronomiski lieliem skaitļiem, kas apgrūtina
starprezultātu pārskatāmību un psiholoģisko uzticību.