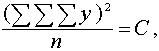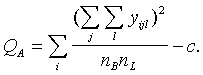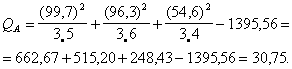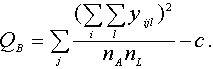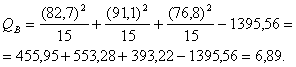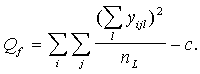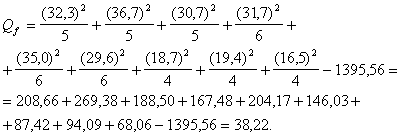8. Dispersijas analīze
8.1.
Vienkāršā jeb vienfaktora dispersijas analīze
8.1.1.
Dispersijas analīzes būtība un uzdevumi
Dispersijas
analīzes būtību zināmā mērā atklāj tās nosaukums. Tā ir analīzes metode, ar
kuru pēta kādas pazīmes dispersiju. Izdarīt dispersijas analīzi nozīmē sadalīt
dispersiju sastāvdaļās jeb komponentēs un tās salīdzināt.
Dispersijas
analīzi visbiežāk lieto statistisko hipotēžu pārbaudei un secinājumu
matemātiskai argumentācijai. Galvenā tās atšķirība no iepriekšējā nodaļā
aplūkotajām metodēm ir šāda. Iepriekšējā nodaļā salīdzinājām divu izlašu
vidējos, relatīvos biežumus, dispersijas; tāpat divus sadalījumus: empīrisko un
teorētisko. Dispersijas analīze ļauj pārbaudīt hipotēzes par vairāku izlašu
(grupu) līdzību vai atšķirību.
Tā
kā dispersijas analīze dod iespēju pārbaudīt hipotēzes par grupās sadalītu
statistisko kopu, to var uzlūkot par grupēšanas loģisku turpinājumu. Tomēr
dispersijas analīze nav obligāti jāsaista ar grupēšanu. Var pārbaudīt arī
hipotēzes par tādām kopas daļām, piemēram, klasēm, kuras izdalītas
klasifikācijas rezultātā un par kurām savākti dati, veicot patstāvīgus
novērojumus.
Dispersijas
analīzi var lietot analītiskā grupējuma novērtēšanai. Izdarot
analītisko grupēšanu, statistisko kopu sagrupē pēc vienas pazīmes un par katru
grupu aprēķina kādas citas pazīmes vidējo lielumu. Šāds grupējums dod iespēju
konstatēt, vai starp abām pazīmēm eksistē sakarības un kāds ir šo sakarību
raksturs. Ja gupējums izdarīts pēc faktorālās pazīmes, tad var aprēķināt
rezultatīvās pazīmes šādas dispersijas:
- kopējo jeb parasto dispersiju ![]() kas raksturo datu
variāciju ap visas kopas aritmētisko
kas raksturo datu
variāciju ap visas kopas aritmētisko
vidējo;
-
izskaidroto jeb faktorālo dispersiju ![]() kas raksturo grupu
aritmētisko vidējo variāciju ap
kas raksturo grupu
aritmētisko vidējo variāciju ap
visas
kopas vidējo;
-
atlikušo jeb neizskaidroto dispersiju ![]() kas raksturo datu
variāciju ap attiecīgo grupu
kas raksturo datu
variāciju ap attiecīgo grupu
vidējiem.
Ja
izskaidrotā dispersija ir relatīvi liela, bet neizskaidrotā maza, tas nozīmē,
ka grupēsanas pazīme ir cieši saistīta ar to pazīmi, kuras dispersiju analizē,
- un otrādi. Tādēļ dispersijas analīzi var izmantot sakarību statistiskās nozīmības pētīšanai, noskaidrojot, vai šīs sakarības ir
nozīmīgas vai arī tās radušās gadījuma rakstura cēloņu dēļ.
Daži
uzdevumi, kuru risināšanai var lietot dispersijas analīzi.
1.
Noskaidrot, vai strādnieku izglītība būtiski ietekmē darba ražīgumu. Ja
izglītību reģistrē, izmantojot tikai divas gradācijas, tādu uzdevumu var
atrisināt ar nulles hipotēzes pārbaudi. Ja turpretī izdala vairākas gradācijas,
tad ar hipotēžu pārbaudi var salīdzināt savā starpā jebkuras divas gradācijas,
bet grūti salīdzināt visas gradācijas vienlaikus. Tādu uzdevumu var atrisināt
dispersijas analīze.
2.
Noskaidrot, vai kādas preces, piemēram, apģērbu pieprasījums, rēķinot uz vienu
iedzīvotāju, dažādos apvidos atšķiras būtiski. Arī šajā gadījumā, ja izdala
tikai divas teritoriālas grupas, piemēram, pilsētas un laukus, var lietot
vienkāršu hipotēzes pārbaudi. Ja izdalīto apvidu ir vairāk, tad izdevīgāk lietot
dispersijas analīzi.
3.
Noskaidrot, vai studentu sekmība visos augstskolas kursos ir aptuveni vienāda
vai arī tā atšķiras būtiski.
Dispersijas
analīzi plaši lieto dažādu eksperimentu un izmēģinājumu novērtēšanā.
Dispersijas
analīzes tipveida shēma satur šādas darbības:
1)
noviržu kvadrātu summas sadalīšanu komponentēs;
2)
brīvības pakāpju skaita sadalīšanu komponentēs;
3)
dispersiju aprēķināšanu uz vienu brīvības pakāpi;
4)
dispersiju attiecības F atrašanu;
5) F robežvērtības
atrašanu matemātiskajās tabulās, ņemot vērā vajadzīgo nozīmības līmeni,
empīriskās F attiecības salīdzināšanu ar kritisko
robežu un lēmuma pieņemšanu.
8.1.2. Noviržu
kvadrātu summmas sadalīšana
Dispersijas
analīzē dispersijas aprēķina, noviržu kvadrātu summu dalot ar brīvības pakāpju skaitu.
Tādēļ ir nepieciešams sadalīt komponentēs atsevišķu noviržu kvadrātu summu un
attiecīgi - brīvības pakāpju skaitu. Pēc tam var izpildīt dalīšanas operāciju.
Šajā
paragrāfā pievērsīsimies noviržu kvadrātu
summas sadalīšanai izskaidrotajā
un neizskaidrotajā daļā, ja dalījuma pamatā ir grupējums. Nākošais paragrāfs
veltīts brīvības pakāpju sadalīšanai.
Noviržu
kvadrātu summas dispersijas analīzē parasti apzīmē ar Q, pie tam Q bez
indeksa nozīmē kopējo noviržu kvadrātu summu, ![]() atlikušo jeb
neizskaidroto noviržu kvadrātu summu. Faktorus, resp. grupēšanas pazīmes
dispersijas analīzē pieņemts apzīmēt ar alfabēta pirmajiem burtiem. Tādēļ, ja
grupējums ir izdarīts pēc vienas pazīmes, izskaidroto jeb faktorālo noviržu
kvadrātu summu apzīmē ar
atlikušo jeb
neizskaidroto noviržu kvadrātu summu. Faktorus, resp. grupēšanas pazīmes
dispersijas analīzē pieņemts apzīmēt ar alfabēta pirmajiem burtiem. Tādēļ, ja
grupējums ir izdarīts pēc vienas pazīmes, izskaidroto jeb faktorālo noviržu
kvadrātu summu apzīmē ar ![]() Var izmantot arī
skaitļu indeksus, piem.,
Var izmantot arī
skaitļu indeksus, piem., ![]() .
.
Noviržu
kvadrātu summas vienfaktora dispersijas analīzē saista šāda sakarība:
![]() (8.1)
(8.1)
Sākotnējo
informāciju, ko izmanto noviržu kvadrātu summas sadalīšanai, ir lietderīgi
sakārtot šādā tabulā.
8.1.
tabula
Sākotnējā
informācija dispersijas analīzei
|
Grupas, grupējot pēc
faktora A |
Novērojumi |
|
|
|
|
|
|
|
|
|
|
... |
... ... ... ...
... ... |
|
|
|
|
... |
... ... ... ...
... ... |
|
|
|
|
|
|
Noviržu kvadrātu summas
var aprēķināt kā ar noviržu, tā arī ar momentu metodi.
Noviržu
metode labāk atklāj aprēķinu būtību un ir uzskatāma par pamatmetodi. No
skaitļošanas darba samazināšanas viedokļa priekšrocības ir momentu metodei,
tādēļ to plaši lieto praksē.
Izmantojot
noviržu metodi, noviržu kvadrātu summas atrod pēc
šādām pamatformulām (8.2.):
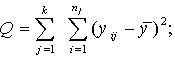 (8.2)
(8.2)
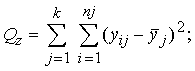
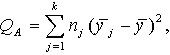
kur
![]() faktiskais
rezultatīvās pazīmes lielums (datu kopas elements) i - tajā
faktiskais
rezultatīvās pazīmes lielums (datu kopas elements) i - tajā
kopas vienībā, kura
ietilpst j - tajā
grupā;
![]() j - tās grupas aritmētiskais vidējais;
j - tās grupas aritmētiskais vidējais;
![]() visas kopas
aritmētiskais vidējais;
visas kopas
aritmētiskais vidējais;
![]() j - tās grupas pēdējās vienības numurs
(arī vienību skaits j - tajā
j - tās grupas pēdējās vienības numurs
(arī vienību skaits j - tajā
grupā);
![]() pēdējās grupas
numurs (arī grupu skaits pētījamā kopā);
pēdējās grupas
numurs (arī grupu skaits pētījamā kopā);
![]() kopas vienību
skaits,
kopas vienību
skaits, 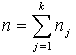 .
.
Momentu metodes formulas, pēc kurām var
izskaitļot ![]() ir dotas 8.2. tabulā (nākošā lpp.).
ir dotas 8.2. tabulā (nākošā lpp.).
Lai
vienkāršotu momentu metodes formulu pierakstu, dažreiz izmanto šādus
apzīmējumus:
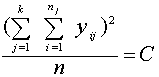 ; šo lielumu sauc par korekcijas locekli;
; šo lielumu sauc par korekcijas locekli;
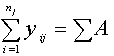 - atsevišķas grupas
datu summa;
- atsevišķas grupas
datu summa;
![]() - atsevišķas grupas
datu kvadrātu summa;
- atsevišķas grupas
datu kvadrātu summa;
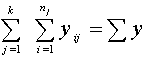 - visas kopas datu
summa;
- visas kopas datu
summa;
![]() - visas kopas datu
kvadrātu summa.
- visas kopas datu
kvadrātu summa.
Tad
momentu metodes formulas var pierakstīt tā, kā tas izdarīts 8.2.tabulas pēdējā
ailē.
8.2. tabula
Noviržu kvadrātu
summu aprēķināšanas formulas
|
Rādītāji |
Noviržu |
Momentu metode |
|
|
(noviržu kvadrātu
summas) |
metode |
ar pilnu pierakstu |
ar vienkāršotu
pierakstu |
|
Kopējā
|
|
|
|
|
Izskaidrotā
|
|
|
|
|
Neizskaidrotā
(grupu iekšējā) |
|
|
|
Piemērs. Nejauši izvēloties, izraudzīti divpadsmit
strādnieki ar dažādu izglītību un fiksēts viņu darba ražīgums. Izglītība dalīta
trīs grupās: 1) pamatizglītība, 2)
nepabeigta vidējā, 3) vidējā un augstākā. Reģistrētais darba ražīgums ir
parādīts 8.3. tabulā.
Jānoskaidro,
vai izglītības ietekme uz darba ražīgumu ir būtiska, vai arī to var izskaidrot
ar nejaušību.
|
Aprēķināsim
aritmētiskos vidējos |
|
|
8.3.
tabula |
|
|
|
|
Divpadsmit
strādnieku darba ražīgums |
||
|
Varētu secināt, ka augstāks izglītības |
|
|
|
|
|
līmenis nodrošina augstāku darba ražīgumu. Tomēr,
ņemot vērā, ka izlase ir |
|
Izglītības līmenis (grupas) |
Darba ražīgums (novērojumi) |
|
|
ļoti maza un
katras grupas ietvaros vē- |
|
|
|
|
|
rojama diezgan liela variācija, pārbau- |
|
Pamatskolas |
3 2
4 3 |
|
|
dīsim šī
secinājuma pareizību ar disper- |
|
Nepabeigtā
vidējā |
4 3
5 4 |
|
|
sijas
analīzes metodēm. |
|
Vidējā un
augstākā |
4 6
5 5 |
|
|
|
|
|
|
|
Šai
nolūkā izvirza dispersijas analīzes nulles hipotēzi, ka ģenerālā kopā grupu
vidējie ir vienādi. Uzdevums ir
pārbaudīt, vai šo hipotēzi var noraidīt ar pietiekami augstu varbūtību, vai
nevar noraidīt.
Noviržu
kvadrātu summas var aprēķināt pēc noviržu metodes, kuras formulas ir loģiski saprotamākas, bet dažreiz
darbietilpīgākas. Tā, piemēram,
noviržu kvadrātu summa no grupas aritmētiskā vidējā pirmajai grupai ir
![]() .
.
Līdzīgi
aprēķina noviržu kvadrātu summas otrajai un trešajai grupai. Piemēram šo summu
vērtības ir 2 un 2.
Kopējo
neizskaidroto jeb intragrupu noviržu kvadrātu
summu ![]() var aprēķināt,
summējot noviržu kvadrātu summu pa visām grupām:
var aprēķināt,
summējot noviržu kvadrātu summu pa visām grupām:
![]()
Noviržu
kvadrātu summu no kopējā aritmētiskā vidējā var aprēķināt šādi:
![]()
Izskaidroto jeb starpgrupu noviržu kvadrātu summu
![]() var aprēķināt, atņemot
no kopējās noviržu kvadrātu summas intragrupu noviržu kvadrātu summu:
var aprēķināt, atņemot
no kopējās noviržu kvadrātu summas intragrupu noviržu kvadrātu summu:
![]()
Piemērā ![]() Piebildīsim, ka
Piebildīsim, ka ![]() var aprēķināt arī
tieši:
var aprēķināt arī
tieši:
![]()
8.4. tabulā (sk. nāk. lpp) parādīti
noviržu kvadrātu summu izskaitļojumi, izmantojot momentu metodi.
Kopējā noviržu kvadrātu
summa ir:
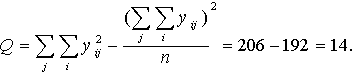
Neizskaidrotā
(grupu iekšējā) noviržu kvadrātu summa ir
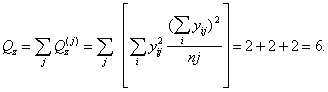
Izskaidrotā noviržu summa ir
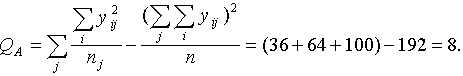
8.4. tabula
Darba tabula noviržu
kvadrātu summu aprēķināšanai
ar momentu metodi
|
Grupas j |
Sākot- nējie dati
|
Datu kvadrāti
|
Summu kvadrāti
|
Vidējie summu
kvadrāti
|
Noviržu kvadrātu
summas grupu ietvaros
|
|
|
|
|
|
|
|
|
1. |
3
|
9 |
|
|
|
|
|
2 |
4 |
|
|
|
|
|
4 |
16 |
|
|
|
|
|
3 |
9 |
|
|
|
|
|
12 |
38 |
|
144
: 4 = 36 |
38
- 36 = 2 |
|
|
|
|
|
|
|
|
2. |
4 |
16 |
|
|
|
|
|
3 |
9 |
|
|
|
|
|
5 |
25 |
|
|
|
|
|
4 |
16 |
|
|
|
|
|
16 |
66 |
|
256
: 4 = 64 |
66
- 64 = 2 |
|
|
|
|
|
|
|
|
3. |
4 |
16 |
|
|
|
|
|
6 |
36 |
|
|
|
|
|
5 |
25 |
|
|
|
|
|
5 |
25 |
|
|
|
|
|
20 |
102 |
|
400
: 4 = 100 |
102
- 100 = 2 |
|
|
48 |
206 |
|
2304 : 12 =192 |
|
Var
izdarīt šādu pārbaudi: ![]() ; 14 = 6 + 8.
; 14 = 6 + 8.
Bieži
dispersijas analīzē aprēķina kopējo noviržu kvadrātu summu Q un izskaidroto jeb starpgrupu noviržu kvadrātu
summu ![]() , bet neizskaidroto
jeb atlikušo noviržu kvadrātu summu
, bet neizskaidroto
jeb atlikušo noviržu kvadrātu summu ![]() iegūst kā starpību:
iegūst kā starpību:
![]()
No tā arī radies ![]() nosaukums. Piemērā
nosaukums. Piemērā
![]() = 14 - 8 = 6 .
= 14 - 8 = 6 .
Kā
redzams, rezultāti, kas iegūti ar noviržu metodi, sakrīt ar rezultātiem, kas
iegūti ar momentu metodi, tādēļ ir iespējams izvēlēties to metodi, kura
konkrētajā gadījumā šķiet vienkāršāka.
8.1.3. Brīvības pakāpju skaita sadalīšana
Dispersijai,
ko aprēķina datu novirzēm no kopējā aritmētiskā vidējā, ir n -1 brīvības pakāpe. Starpgrupu dispersiju jeb
izskaidroto dispersiju veido grupu vidējo novirzes no kopējā aritmētiskā
vidējā. Tādēļ šai dispersijai ir k - 1 brīvības
pakāpe, kur k ir izdalīto grupu skaits. Neizskaidroto jeb
intragrupu dispersiju veido individuālo datu
novirzes no grupu vidējiem. Tādēļ
atsevišķi ņemtā grupā tai ir nj -1 brīvības pakāpe, kur
nj ir vienību (datu) skaits j - tajā grupā. Kopējais intragrupu dispersijas brīvības
pakāpju skaits visās grupās ir ![]() , kur k ir izdalīto grupu skaits. Summējot katru
locekli atsevišķi, dabūjam, ka brīvības pakāpju skaits n ir
, kur k ir izdalīto grupu skaits. Summējot katru
locekli atsevišķi, dabūjam, ka brīvības pakāpju skaits n ir
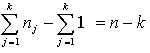 . Tādēļ var rakstīt,
ka brīvības pakāpju skaits
. Tādēļ var rakstīt,
ka brīvības pakāpju skaits
visai dispersijai n
= n - 1 ;
(8.3)
starpgrupu
dispersijai nA = k - 1 ; (8.4)
intragrupu
dispersijai nZ = n - k .
(8.5)
Tādējādi kopējais brīvības pakāpju
skaits ir sadalīts komponentēs:
n = nA+ nZ , (8.6)
jo n - 1 = k -
1 + n - k = n - 1.
Piemērā n = n - 1 = 12 - 1 = 11 ;
nA = k - 1 = 3 - 1 =
2 ;
nZ = n - k = 12 - 3
= 9 .
8.1.4. Dispersiju attiecības aprēķināšana
un novērtēšana
Pēc tam kad noviržu kvadrātu summa un
brīvības pakāpes ir sadalītas, aprēķina dispersijas uz vienu brīvības pakāpi :
![]() ; (8.7)
; (8.7)
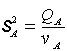 ; (8.8)
; (8.8)
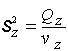 , (8.9)
, (8.9)
kur ![]() - kopējā dispersija;
- kopējā dispersija;
![]() - izskaidrotā jeb faktorālā dispersija;
- izskaidrotā jeb faktorālā dispersija;
![]() - neizskaidrotā dispersija.
- neizskaidrotā dispersija.
Jāievēro,
ka ![]() , jo, aprēķinot šīs dispersijas, nav ņemts viens un tas pats
dalītājs, kā to dara dispersiju saskaitīšanas teorēmā, bet dažādi dalītāji -
katrai dispersijai savs brīvības pakāpju skaits.
, jo, aprēķinot šīs dispersijas, nav ņemts viens un tas pats
dalītājs, kā to dara dispersiju saskaitīšanas teorēmā, bet dažādi dalītāji -
katrai dispersijai savs brīvības pakāpju skaits.
Piemērā: ![]() ;
; ![]() ;
; ![]()
Tagad
dispersijas analīzes nulles hipotēzi var komentēt citā aspektā. Ja nulles hipotēze ir pareiza,
tad noviržu kvadrātu summām ![]() un
un ![]() jābūt aptuveni
proporcionālām atbilstošajām brīvības pakāpēm; resp., abām dispersijām, rēķinātām uz vienu brīvības
pakāpi, jābūt aptuveni vienādām. Salīdzinot
jābūt aptuveni
proporcionālām atbilstošajām brīvības pakāpēm; resp., abām dispersijām, rēķinātām uz vienu brīvības
pakāpi, jābūt aptuveni vienādām. Salīdzinot ![]() un
un ![]() , var spriest, vai pazīme, pēc kuras ir izdarīts grupējums,
ir saistīta ar otru statistisko pazīmi, vai nav saistīta ar to. Ja grupējums
izdarīts pēc faktorālās pazīmes, var spriest, vai tā rezultatīvo pazīmi būtiski
ietekmē vai neietekmē.
, var spriest, vai pazīme, pēc kuras ir izdarīts grupējums,
ir saistīta ar otru statistisko pazīmi, vai nav saistīta ar to. Ja grupējums
izdarīts pēc faktorālās pazīmes, var spriest, vai tā rezultatīvo pazīmi būtiski
ietekmē vai neietekmē.
Ja nulles hipotēze ir pareiza, vienādība ![]() praktiski realizējas
tikai tad, ja izlase ir ļoti liela (robežgadījumā - bezgalīga).
Reālās izlasēs viena no dispersijām vienmēr ir lielāka nekā otra.
praktiski realizējas
tikai tad, ja izlase ir ļoti liela (robežgadījumā - bezgalīga).
Reālās izlasēs viena no dispersijām vienmēr ir lielāka nekā otra.
Tādēļ
dispersijas analīzē pati svarīgākā nozīme ir izskaidrotās
un neizskaidrotās dispersijas attiecībai,
ko apzīmē ar burtu F :
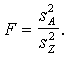 (8.10)
(8.10)
Piemērā ![]()
Lai
noskaidrotu, vai faktorālā pazīme, pēc kuras grupēta kopa, būtiski ietekmē
rezultatīvo pazīmi, aprēķinātā attiecība F
jāsalīdzina ar kritisko vērtību pēc
tabulām. Ja izvēlas nozīmības līmeni ![]() , tad F tabulās
var atrast kritisko vērtību 4,26. Attiecības F empīriskā
vērtība ir 5,97, tātad lielāka par
tabulas vērtību. Tādēļ nulles hipotēzi
ir iespējams noraidīt ar varbūtību
augstāku par 0,95. Izglītības
ietekme uz darba ražīgumu ir statistiski nozīmīga.
, tad F tabulās
var atrast kritisko vērtību 4,26. Attiecības F empīriskā
vērtība ir 5,97, tātad lielāka par
tabulas vērtību. Tādēļ nulles hipotēzi
ir iespējams noraidīt ar varbūtību
augstāku par 0,95. Izglītības
ietekme uz darba ražīgumu ir statistiski nozīmīga.
Dispersijas
analīzē, tāpat kā jebkurā citā statistikas pētījumā, vēlams ņemt pietiekami
lielas izlases kopas. Ja, piemēram,
iepriekšējā uzdevumā no katras grupas izslēdz pēdējo strādnieku, kura izstrāde
sakrīt ar ar grupas vidējo izstrādi, tad grupējuma kopaina nemainās, jo
nemainās ne grupu vidējais, ne kopējais vidējais, ne arī grupu
dispersijas. Nemainītos arī secinājumi,
kādus izdarītu ekonomiskās statistikas kursā. Tomēr
dispersijas analīzē iegūst citus rezultātus. Nav grūti izrēķināt,
ka šādā gadījumā F=3, bet F0,95= 5,14. Tātad F< F0,95
un nulles hipotēzi noraidīt nevar; izglītības ietekme uz
darba ražīgumu paliek nepierādīta.
Tāpat
svarīgi ir pamatot praktiski nepieciešamo
hipotēzes pārbaudes nozīmības līmeni.
Ja izvirzīto hipotēzi grib pārbaudīt
ar nozīmības līmeni 0,01, tad sākotnējam piemēram par 12 strādnieku grupu F0,01=
8,02. Faktiskais F= 5,97. Tātad F < F0,01 un
nulles hipotēze paliek spēkā. Ar varbūtību 0,99 nevar apgalvot, ka dati par 12
strādniekiem pierāda izglītības ietekmi uz darba ražīgumu. Ja ir vajadzīgs tik
augsts nozīmības līmenis, jāņem lielāka izlase.
F kritērijs parāda, ka atšķirības starp
grupu vidējiem lielumiem (piemērā - darba ražīgumu atsevišķās grupās) ir
statistiski nozīmīgas ar varbūtību 0,95.
Papildus vēl var noskaidrot, tieši starp kuriem
vidējiem ir šīs nozīmīgās atšķirības, jo dažu grupu vidējo atšķirības var būt
arī nenozīmīgas.
Šo
uzdevumu risina, vadoties no pieņēmuma, ka visai kopai ir raksturīga
kopēja intragrupu dispersija ![]() , kas raksturo variāciju ar grupu vidējiem.
, kas raksturo variāciju ar grupu vidējiem.
Piemērā,
![]() =0,6667.
=0,6667.
Aprēķinot
kvadrātsakni, iegūstam standartnovirzi ![]() . Tā kā katras grupas vidējais ir aprēķināts no 4
novērojumiem, tad, lai aprēķinātu šī vidējā standartkļūdu, standartnovirze ir
jādala ar
. Tā kā katras grupas vidējais ir aprēķināts no 4
novērojumiem, tad, lai aprēķinātu šī vidējā standartkļūdu, standartnovirze ir
jādala ar ![]() . Tādējādi
. Tādējādi ![]() = 0,8165 : 2 = 0,4082. Tā kā gribam salīdzināt savā starpā
divus vidējos, ir jāatrod starpības
= 0,8165 : 2 = 0,4082. Tā kā gribam salīdzināt savā starpā
divus vidējos, ir jāatrod starpības ![]() standartkļūda, kuru
aprēķina pēc iepriekšējā nodaļā parādītās formulas
standartkļūda, kuru
aprēķina pēc iepriekšējā nodaļā parādītās formulas
![]() .
.
Bet, ja pieņem, ka visu vidējo
standartkļūdas ir vienādas, tad
![]()
Piemērā
![]()
![]() .
.
Tā
kā dispersijas analīzes pamatjautājums tika pārbaudīts ar nozīmības līmeni ![]() , tad ar šo pašu nozīmības līmeni jāpārbauda aritmētisko
vidējo starpības nozīmīgums. Tabulās
atrod, ka
, tad ar šo pašu nozīmības līmeni jāpārbauda aritmētisko
vidējo starpības nozīmīgums. Tabulās
atrod, ka ![]() . Pareizinot vidējo
starpības standartkļūdu ar koeficientu t,
iegūst vismazāko kritisko jeb vismazāko būtisko starpību,
ko parasti apzīmē ar simbolu , norādot pie tā
nozīmības līmeni:
. Pareizinot vidējo
starpības standartkļūdu ar koeficientu t,
iegūst vismazāko kritisko jeb vismazāko būtisko starpību,
ko parasti apzīmē ar simbolu , norādot pie tā
nozīmības līmeni:
![]()
![]() .
.
Par
būtiskām ir uzskatāmas tās aritmētisko vidējo starpības, kas pārsniedz šo
līmeni. Salīdzinot ar vismazāko kritisko starpību, redzams, ka
statistiski nozīmīgi atšķiras darba ražīgums 1. un 3. grupā, turpretī
atšķirības blakus esošajās grupās nav nozīmīgas.
Faktiskās
aritmētisko vidējo starpības var sakārtot tabulā. Statistiski nozīmīgās
starpības tabulā izceļ, tās pasvītrojot
vai liekot zvaigznīti.
8.5. tabula
Aritmētisko vidējo
starpības
|
|
|
|
|
|
1 |
2 |
|
|
- |
1 |
8.1.5. Analītiskā grupējuma dispersijas analīze
Analītiskos
grupējumus parasti publicē tādā formā, kā parādīts 8.6 tabulas pirmajās trīs
ailēs. Ja nav pieejami sākotnējie dati,
kas izmantoti šī grupējuma izstrādei, vai arī nav iespējams organizēt sākotnējo
datu atkārtotu apstrādi, dispersijas analīzi var izmantot grupējumā atspoguļoto
sakarību tuvinātai
matemātiskai novērtēšanai. Ja sākotnējo datu apstrāde ir iespējama, pētot
sakarības starp kvantitatīvām nepārtrauktām pazīmēm, ieteicams izmantot
regresijas un korelācijas analīzes metodes, kas ir nākošo grāmatas nodaļu
saturs.
8.6. tabula
Analītiskais
grupējums, kurš rāda kartupeļu stādījumu platības ietekmi uz ražību,
un starpgrupu
noviržu kvadrātu summas aprēķins
|
Saimniecību |
Saimniecību |
Vidējā |
Aprēķināmie dati |
||
|
grupas pēc
stādījumu platības (ha) |
skaits |
ražība |
|
|
|
|
|
|
|
|
|
|
|
līdz 8 |
10 |
115 |
-
10 |
100 |
1
000 |
|
8 - 15 |
20 |
120 |
-
5 |
25 |
500 |
|
15 - 25 |
40 |
120 |
-
5 |
25 |
1
000 |
|
25 - 40 |
20 |
130 |
+
5 |
25 |
500 |
|
virs 40 |
10 |
140 |
+ 15 |
225 |
2 250 |
|
K o p ā |
100 |
X |
X |
X |
5
250 |
|
V i d ē j i |
X |
125 |
X |
X |
X |
Izmantojot
analītisko grupējumu (8.6.tabula), var tuvināti aprēķināt starpgrupu jeb izskaidroto noviržu kvadrātu summu. Par statistiskajiem svariem jāņem kopas
vienību skaits grupās. Šie svari var nesakrist ar svariem, kuri lietoti,
aprēķinot aritmētisko vidējo.
Piemērā,
izstrādājot analītisko grupējumu, vidējā ražība būtu jānosaka, par
statistiskajiem svariem ņemot nevis
saimniecību skaitu, bet sējumu platību. Tā arī parasti dara. Tālāk apstrādājot
grupējuma rezultātus, šie statistiskie svari bieži nav zināmi. Tādēļ par
svariem jāņem saimniecību skaits grupās. Ja visas saimniecības ir kvalitatīvi
vienveidīgas un kopa nav maza, šāda rīcība lielas kļūdas nerada.
Starpgrupu
jeb izskaidroto noviržu kvadrātu summas aprēķina vai nu pēc noviržu, vai
momentu metodes. Šajā gadījumā ērtāk
lietot noviržu metodi, jo grupu skaits ir neliels, kopējais
aritmētiskais vidējais ir zināms un
grupu vidējo novirzes no kopējā vidējā ir nelieli veseli skitļi. Turpret, lietojot momentu metodi, ![]() būtu ļoti lieli
skaitļi.
būtu ļoti lieli
skaitļi.
Aprēķini,
lietojot noviržu metodi, parādīti 8.6. tabulas pēdējās ailēs. Atsevišķās ailēs
aprēķina novirzes ![]() , to kvadrātus
, to kvadrātus ![]() un šo kvadrātu
reizinājumus ar statistiskajiem svariem
un šo kvadrātu
reizinājumus ar statistiskajiem svariem ![]() . Pēdējās ailes summa ir meklētā starpgrupu noviržu kvadrātu
summa
. Pēdējās ailes summa ir meklētā starpgrupu noviržu kvadrātu
summa ![]() . Piemērā
. Piemērā
![]() = 5 250.
= 5 250.
Grupējumā
var būt nevienādi vai nenoslēgti intervāli, ja vien visu intervālu jeb grupu
aritmētiskie vidējie ![]() , kā arī visas kopas
vidējais
, kā arī visas kopas
vidējais ![]() ir aprēķināti
pareizi. Kā jau bija teikts, dispersijas
analīzi var lietot pat tad, ja grupas izdalītas pēc atributīvas pazīmes.
ir aprēķināti
pareizi. Kā jau bija teikts, dispersijas
analīzi var lietot pat tad, ja grupas izdalītas pēc atributīvas pazīmes.
Var
aprēķināt brīvības pakāpju skaitu, kas attiecas uz starpgrupu noviržu kvadrātu
summu: nA = k - 1 = 5 - 1
= 4.
Līdz ar to ir iespējams aprēķināt dispersiju uz vienu
brīvības pakāpi:
![]() .
.
Lai
atrastu dispersijas analīzei vajadzīgo neizskaidroto
jeb intragrupu noviržu kvadrātu summu, vajadzīga kopējā noviržu kvadrātu summa.
Kopējās noviržu kvadrātu summas aprēķināšanai bieži
var izmantot datus, kuri publicēti kādā citā tabulā statistisko datu krājumā.
Tādi dati parādīti 8.7. tabulas pirmajās divās ailēs. Izmantojot vienam
uzdevumam divu dažādu tabulu datus, vienmēr jāpārliecinās, vai tās raksturo
vienu un to pašu kopu un vai kopas vienību skaits abās tabulās ir vienāds.
Ja
šādi dati ir pieejami, noviržu kvadrātu summu aprēķina pēc noviržu metodes, kā
tas parādīts 8.7. tabulas pēdējās trīs ailēs. Arī šis aprēķins ir tuvināts, jo
tā pamatā ir pieņēmums, ka saimniecību sadalījums pēc ražības grupu ietvaros ir
vienmērīgs.
8.7. tabula
Saimniecību
sadalījums pēc kartupeļu ražības
un noviržu kvadrātu
summas aprēķins
|
Saimniecību |
Saimniecību |
Intervālu |
Aprēķināmie dati |
||
|
grupas pēc ražības (cnt/ha) |
skaits |
centri
|
|
|
|
|
|
|
|
|
|
|
|
60 ... 80 |
5 |
70 |
-
55 |
3
025 |
15
125 |
|
80 ... 100 |
10 |
90 |
-
35 |
1
225 |
12
250 |
|
100 ... 120 |
30 |
110 |
-
15 |
225 |
6
750 |
|
120 ... 140 |
25 |
130 |
+
5 |
25 |
625 |
|
140 ... 160 |
20 |
150 |
+ 25 |
625 |
12
500 |
|
160 ... 180 |
10 |
170 |
+ 45 |
2 025 |
20 250 |
|
K o p ā |
100 |
X |
X |
X |
67
500 |
|
V i d ē j i |
X |
125 |
X |
X |
X |
Piemērā kopējā noviržu kvadrātu summa ir 67 500. Tai atbilst n - 1
= 100 - 1 = 99 brīvības pakāpes. Noviržu kvadrātu
summu, kas ar analītisko grupējumu nav
izskaidrota, jeb intragrupu noviržu
kvadrātu summu ![]() aprēķina kā
kopējās noviržu kvadrātu summas
67500 un izskaidrotās noviržu kvadrātu summas 5250 starpību. Tātad intragrupu
noviržu kvadrātu summa
aprēķina kā
kopējās noviržu kvadrātu summas
67500 un izskaidrotās noviržu kvadrātu summas 5250 starpību. Tātad intragrupu
noviržu kvadrātu summa ![]() = 67500 - 5250 = 62 250
un ir saistīta ar nZ = n - k = 100 - 5 =
95 brīvības pakāpēm.
= 67500 - 5250 = 62 250
un ir saistīta ar nZ = n - k = 100 - 5 =
95 brīvības pakāpēm.
Rēķinot uz vienu brīvības pakāpi,
iegūstam, ka ![]() , bet dispersiju attiecība
, bet dispersiju attiecība
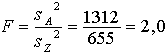 .
.
Šī
attiecība jāsalīdzina ar tabulas vērtību, kura atbilst 4 un 95 brīvības
pakāpēm.
Izvilkums no tabulas ir šāds
(uzrādītas 0,05 un 0,01 nozīmības līmeņiem atbilstošās kritiskās vērtības):
Lielākā noviržu kvadrātu
summa ![]() atbilst 4 brīvības
pakāpēm.
atbilst 4 brīvības
pakāpēm.
|
v1 |
|
|
Nulles hipotēzi,
kas apgalvo, ka stādījumu platībai
nav būtiskas |
|
|
4 |
|
ietekmes
uz ražību, varētu noraidīt ar varbūtību 0,95, ja faktiskā |
|
v2 |
|
|
dispersiju attiecība F pārsniegtu 2,47. |
|
|
|
|
|
|
95 |
2,47 |
|
Lai to pašu hipotēzi noraidītu ar
varbūtību 0,99, šai attiecībai ir |
|
|
3,53 |
|
jābūt lielākai par 3,53. Piemērā 2,0<2,47<3,53, tādēļ
nulles |
|
|
|
|
hipotēzi ar šādām varbūtībām
noraidīt nevar. Kaut gan 8.6. tabulā |
|
|
|
|
bija
redzama vizuāli pārliecinoša sakarība,
tā izrādās statistiski |
nenozīmīga. Cēlonis ir ļoti lielā neizskaidrotā ražības variācija šīs kopas
saimniecībās.
8.2. Daudzfaktoru dispersijas analīze
8.2.1. Daudzfaktoru dispersijas analīzes uzdevumi, veidi
un darba izpildes secība
Ja
vienkāršā jeb vienfaktora dispersijas analīze izvērtē vienkāršu analītisku
grupējumu, tad daudzfaktoru dispersijas analīzi var uzlūkot par
kombinēta analītiska grupējuma izvērtējumu. Sevišķa nozīme
daudzfaktoru dispersijas analīzei ir tad, ja pētī atributīvu
pazīmju ietekmi uz interesējošo rezultatīvo pazīmi. Tādā gadījumā statistikā plaši lietotā korelācijas un regresijas analīze nav izmantojama.
Daudzfaktoru dispersijas analīze dod atbildi par katra
analīzē ieslēgtā faktora statistisko nozīmību. Bez tam var vēl noskaidrot, vai
nozīmīga ir šo faktoru mijiedarbība.
Turpmāk apskatīsim divu faktoru dispersijas analīzi,
kas ir vienkāršākais daudzfaktoru analīzes gadījums.
Izvirzām
šādu uzdevumu.
Speciāla
lauksaimniecības institūcija pārbauda produktīvo dzīvnieku kvalitāti, labākos
no tiem ieraksta Valsts ciltsgrāmatā un iesaka selekcijas darbā. Piemēram,
izrakstīsim datus par trim aitu šķirnēm. Tās nosauc tā teķa vārdā, kurš pirmais
nodibinājis šo šķirni. Par katru šķirni ņemam nedaudz aitas, kuras pieder šai
šķirnei, un reģistrējam viņu gada vilnas nocirpumu, kg. Lai dati būtu
reprezentatīvāki, ņemam trīs gadu datus
(skat. 8.8. tabulas centrālā daļā).
Protams,
novērojumu (aitu) skaits mūsu uzdevumā ir par mazu praktiski reāliem
secinājumiem. Bet, ja novērojumu skaitu ņemtu simtos, kā tas ir praksē, tad
visus aprēķinu starprezultātus mācību grāmatas ietvaros nevarētu parādīt.
Izmantojot dotos datus, izvirzām uzdevumu novērtēt :
1) vai dažādu šķirņu aitas pēc produktivitātes
atšķiras būtiski;
2) vai atsevišķos
gados ir bijusi būtiski atšķirīga aitu produktivitāte
(ņemot visas šķirnes kopā);
3) vai ir būtiska
šķirņu un gadu ietekmes mijiedarbība,
t.i., vai
kāda šķirne
piemērotāka labvēlīgiem un kāda - nelabvēlīgiem gadiem.
Pirmo
faktoru - šķirni - apzīmēsim ar simbolu A, otro - gadu efektu - ar B.
Pirmā
faktora variantus apzīmēsim ar simboliem A1 ,
A2 , ..., vispārīgā
veidā Ai. Analogi otrā faktora: B1 ,
B2
, ..., vispārīgā veidā Bi .
Aitu numurus vienas šķirnes un gada ietvaros (atkārtojums) apzīmējam ar l1
, l2
, ..., vispārīgā veidā le.
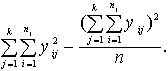
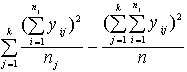
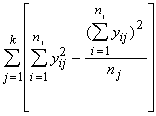
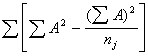
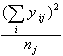
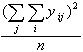
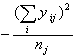
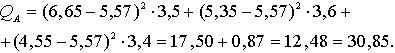
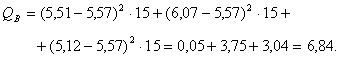
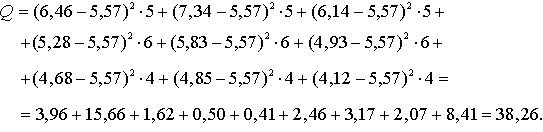
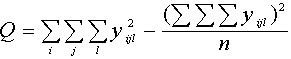 .
.