Ievads daļas 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 attēli 2.3 2.3.2 un d.16_pielikums

14. Dinamikas  rindas

 

14.1. Dinamikas rindas uzbūve, izmaiņu rādītāji un vidējie lielumi

 

14.1.1. Dinamikas rindas un to veidi

 

Par dinamikas rindām sauc skaitļu rindas, kas raksturo statistikas objekta vai parādības izmaiņas laikā. Dinamikas rindu veido divi elementi: laika norādes un līmeņi. Laika norādes var būt laika periodi ( dienas, mēneši, gadi, piecgades) vai laika momenti (mēnešu, gadu utt. pirmās vai pēdējās dienas). Rindu līmeņi izsaka pētāmā objekta vai parādības lielumu norādītajos laika periodos vai momentos.

 Dinamikas rindas sakārto tabulās. Vienkāršākajā gadījumā tabulai ir divas ailes (vai divas rindas): vienā ieraksta laika norādes, otrā - līmeņus.

Intervālu dinamikas rindas līmeņi izsaka parādības darbību vai rezultātus norādītajos laika periodos. Laika norādes ir laika periodi. Momentu dinamikas rindas līmeņi raksturo parādību norādītajos laika momentos. Laika norādes tā tad ir momenti.

Atkarībā no tā, kādi lielumi ir dinamikas rindas līmeņi, izšķir absolūto lielumu, relatīvo lielumu un vidējo lielumu dinamikas rindas.

Izveidojot dinamikas rindu, jāraugās, lai tās līmeņi būtu salīdzināmi gan teritoriālā ziņā, gan pēc objekta sastāva un citām īpatnībām. Ja dinamikas rindu veido vērtības rādītāji, jāraugās, lai tiktu izmantotas salīdzināmas cenas. Līmeņi vienas dinamikas rindas ietvaros jāuzrāda vienās un tajās pašās vienībās

Dinamikas rindas piemērs ir parādīts 14.1. tabulā. Uzskatāms ir dinamikas rindas grafiskais attēls diagrammas veidā (sk. 14.1. att.). No dinamikas rindas un tās grafiskā attēlā parasti jau bez papildus apstrādes var gūt labu priešstatu par pētītā objekta vai parādības izmaiņām laika gaitā.

Tā, piemēram, pēc 14.1. tabulas datiem redzams, ka studentu skaits augstskolās ir samazinājies  par apmērām 10 tūkstošiem.

                                                                                               

 14.1. tabula

Latvijas augstāko mācību iestāžu studentu skaits

mācības gada sākumā, tūkst.

 

Mācības gads

1980/81

1990/91

1991/92

1992/93

1993/94

1994/95

 

 

 

 

 

 

 

Studentu skaits

47,2

46,0

46,3

41,1

37,5

37,6

 

Datu avots: Latvijas statistikas gadagrāmata 1995.- 139. lpp.

 

Ja dinamikas rindu vēlas turpmāk matemātiski apstrādāt, vēlams, lai visi periodi tajā būtu vienāda ilguma, bet visus momentus šķirtu vienāds laika intervāls.

Ja dinamikas rindas tālāka apstrāde nav paredzēta, tajā var izmantot arī nevienāda ilguma periodus vai dažāda ilguma šķirtus laika momentus. Izmantojot garākas laika atstarpes, parasti saīsina  tabulas sākuma daļu, ka raksturo senāko periodu.

 

 

 

 

 

 

 

 

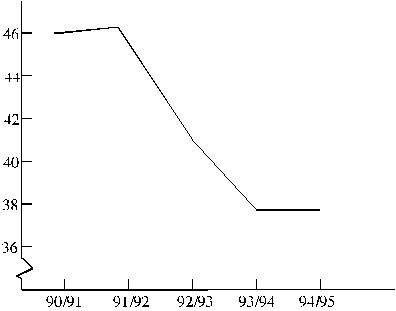
14.1.attēls.  Latvijas augstāko mācības iestāžu studentu skaits, tūkstošos

 

Dinamikas rindas īpatnības dažādās tās daļās labāk izceļ dinamikas izmaiņu rādītāji, kurus sauc arī par dinamikas rindas atvasinātajiem rādītājiem.

 

 

14.1.2. Dinamikas izmaiņu rādītāji

 

Dinamikas rindu izmaiņu rādītājus iegūst, salīdzinot divus dinamikas rindas līmeņus. Ja katru dinamikas rindas līmeni salīdzina ar iepriekšējo līmeni, iegūst ķēdes izmaiņas rādītājus. Ja visus dinamikas rindas līmeņus salīdzina ar rindas pirmo līmeni iegūst bāzes izmaiņu rādītājus. No tā izriet, ka katrai dinamikas rindai var aprēķināt ķēdes un bāzes izmaiņu rādītājus, kuru skaits ir par vienu mazāks nekā līmeņu skaits. Dinamikas izmaiņu rādītājus var sakārtot jaunā dinamikas rindā.

Dinamikas līmeņus var salīdzināt, atņemot vienu līmeni no otra vai dalot vienu līmeni ar otru.

Ķēdes absolūto pieaugumu m(ķ) atrod, atņemot no kārtējā rindas līmeņa   iepriekšējo līmeni  . Bāzes absolūto pieaugumu   atrod, atņemot no kārtējā rindas līmeņa   rindas sākuma  līmeni jeb bāzes līmeni . Absolūtie pieaugumi ir izteikti rindas līmeņu vienībās.

Ķēdes augšanas tempu m(ķ)  atrod,  dalot kārtējo rindas līmeni  ar iepriešējo līmeni  , bet bāzes augšanas tempu   dalot kārtējo rindas līmeni  ar pirmo līmeni 

Augšanas tempi ir izteikti skaitļa viens daļās. Pareizinot tos ar 100, iegūst augšanas tempus procentos.

Ķēdes un bāzes pieauguma tempus  tm(ķ) un tm(b) iegūst no attiecīgajiem  ķēdes un bāzes augšanas tempiem, atņemot 1 (resp.100 %). Pieauguma tempi, tāpat kā augšanas tempi, ir izteikti skaitļa viens daļās vai procentos.

Tā kā ekonomikā dinamikas rindas lielākoties atspoguļo augošus objektus un parādības, izmaiņu rādītājus tradicionāli sauc par pieauguma rādītājiem. Ja dinamikas rinda atspoguļo  dilstošu procesu, absolūtie pieaugumi ir negatīvi, bet aušanas tempi mazāki par 1, resp., par 100 %.

Dinamikas izmaiņu rādītāju aprēķināšanas formulas kopā ar piemēru pēc 14.1. tabulas datiem ir parādītas 14.2. tabulā.

Dinamikas izmaiņu rādītāju interpretācija ir elementāra. Aplūkotajos gados studentu skaits absolūtā izteiksmē  ir samazinājies par 8,4 tūkstošiem. Tas noticis 1992/93. un 1993/94. māc. gados. Pēdējos gados studentu skaits ir stabilizējies.

Viegli konstatēt vienkāršākās matemātiskās sakarības starp dinamikas izmaiņu rādītājiem. Saskaitot ķēdes absolūtos pieaugumus, iegūstam bāzes absolūtos pieaugumus. Reizinot ķēdes augšanas tempus (skaitļa viens daļās), iegūstam bāzes augšanas tempus. Ir iespējama neliela kļūdu uzkrāšanās noapaļošanas rezultātā.

                                                                                                                                                                                                14.2.tabula

 

Latvijas augstskolu studentu skaita izmaiņas

(pēc 14.1. tabulas datiem)

 

 

Rādītāji

Formula        

1990/91

1991/92

1992/93

1993/94

1994/95

Absolūtie pieaugumi,

 

 

 

 

 

 

  tūkstošos:

 

 

 

 

 

 

,
 
ķēdes pieaugums

--

0.3

-5.2

-3.6

 0.1

bāzes pieaugums

--

0.3

-4.9

-8.5

-8.4

Augšanas tempi,   %:

 

 

 

 

 

 

,
 
          ķēdes augšanas             

          temps

 

100

 

100.7

 

88.8

 

91.2

 

100.3

          bāzes augšanas  

           temps

 

100

 

100.7

 

89.3

 

81.5

 

81.7

Pieauguma tempi,%:

 

 

 

 

 

 

,
 

,
 
         ķēdes pieauguma

         temps

 

--

 

0.7

 

-11.2

 

-8.8

 

0.3

         bāzes pieauguma  

         temps

 

--

 

0.7

 

-10.7

 

-18.5

 

-18.3

 

 

14.1.3. Dinamikas rindas vidējie

 

Dinamikas rindas vidējie raksturo dinamikas rindas īpašības visā aplūkojamā periodā. Tāpat kā sadalījuma rindai ir tikai viens aritmētiskais vidējais un viena mediāna, arī katras dinamikas rindas aritmētiskais vidējais ir viens skaitlis, kas raksturo visu rindu.

Dinamikas rindas vidējais līmenis izsaka raksturīgo parādības lielumu rindā ietvertajā laika periodā. Intervālu dinamikas rindas aritmētisko vidējo līmeni  aprēķina, rindas līmeņu summu dalot ar līmeņu skaitu:

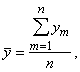                                                                                                                   (14.1)

kur

          -  m-tā perioda līmenis;

          n     - rindas pēdējā locekļa laika norāde.

Ja starp momentu dinamikas rindas līmeņiem ir vienādas laika atstarpes, tad rindas vidējo līmeni tuvināti var aprēķināt pēc formulas

                               

                                                                                          (14.2)

 

Aprēķināsim vidējo studentu skaitu Latvijas augtskolās pēc 14.1. tabulas datiem. Šī ir momentu dinamikas rinda, tādēļ jālieto 14.2. formula. Bez tam jāņem vērā ka rindas pirmo līmeni no otrā šķir desmit reizes ilgāks laika periods nekā pārējos. Šādā gadījumā dinamikas rindas vidējais ir jārēķina vai nu tikai rindas pēdējai daļai, vai jāizmanto ststistiskie svari. kuri ir proporcionāli laika periodam, kuru pārstāv katrs rindas līmenis.

Dinamikas rindas vidējais 1990. - 1995. g. periodam ir

 

 (tūkst.).

 

Vidējais absolūtais pieaugums   izteic, par kādu lielumu vidēji laika vienībā ir izmainījusies pētāmā parādība visā ar  rindu aptvertajā periodā. Definīcijas formulu iegūst, dinamikas rindas ķēžu absolūto pieaugumu summu dalot ar pieaugumu skaitu    :

 

,
 
                                                                                                              (14.3)

 

                   Piemērā:    (tūkst.).

 

Tātad vidēji ik gadus studentu skaits republikas augsskolās samazinājies par 2,1 tūkstošiem.

Izdarot elementārus algebriskus ievietojumus, formulu (14.3) var pārveidot, lai atvieglotu skaitļošanas darbu, ja rinda ir gara.

 

                                                                                                                   (14.4)

 

Piemērā:                           (tūkst.).

 

Vidējo absolūto pieaugumu vēl var izrēķināt pēc formulas

 

                                                    ,                                                             (14.5)

tieši izmantojot rindas pēdējo un pirmo līmeni.

 

Piemērā           (tūkst.).

Vidējais augšanas temps  izteic parādības izmaiņu vidējo intensitāti un to izsaka skaitļa  1 daļās vai procentos. Vidējo augšanas tempu aprēķina, pieņemot, ka visā periodā nosacīti saglabājas viens un tas pats augšanas temps. Citiem vārdiem, ''pieaugums iepriekšējā periodā rada pieaugumu nākošajā periodā''. Lai to nodošinātu, lieto ģeometrisko vidējo . Definīcijas formula ir

 

,
 

,
 

,
 

,
 
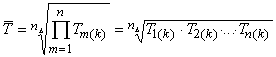                         .                                        (14.6)

 

 Piemērā: .

 

Izdarot algebriskus pārveidojumus, iegūst vienkāršāku formulu

 

                            .                                                                                     (14.7)

 

Piemērā:                

 

To pašu rezultātu var iegūt tieši no rindas līmeņiem pēc formulas

 

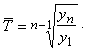                                                                                                                 (14.8)

 

Piemērā :           

 

Ja pēc dažādām formulām aprēķināto vidējo augšanas tempu vērtību pēdējie zīmīgie cipari atšķiras, par precīzāko rezultātu jāuzskata tas, kurš iegūts,  izdarot mazāk darbību (ja darbības visur izpilda ar vienu un to pašu precizitāti).

Vidējo pieauguma tempu  aprēķina, atņemot no vidējā augšanas tempa skaitli 1 (resp. 100%) :                

 

                                        .                                                                               (14.9)

 

Piemērā:   . Vidējais studentu skaita samazinājuma temps norādītajā laika periodā ir 4,9 % gadā.

Dinamikas rindas slīdošos vidējos aprēķina kā vidējos līmeņus trīs līdz septiņas laika vienības (gadus) gariem periodiem, kuri obligāti ir īsāki nekā visa dinamikas rinda. Rēķinot katru nākošo slīdošo vidējo, visvecāko rindas līmeni atmet, bet pievieno vienu jaunu līmeni. Tādējādi atšķirībā  no visiem pārējiem vidējiem iegūst nevis vienu, bet vairākus vidējos, kurus, centrējot pret attiecīgo periodu viduspunktiem, iegūst jaunu dinamikas rindu. Slīdošo vidējo dinamikas rinda parādības izmaiņu pamattendenci atklāj labāk nekā sākotnējo līmeņu rinda, jo, rēķinot slīdošos vidējos,  tiek izslēgtas atsevišķu sākotnējo rindas līmeņu gadījuma rakstura svārstības. Tādēļ uzskata, ka ar slīdošajiem vidējiem var izdarīt dinamikas rindas izlīdzināšanu.

 

 

 

 

 

 

 

14.2. Dinamikas  rindas analītiska  izlīdzināšana

 

14.2.1.Uzdevuma nostādne

 

Aplūkojot dinamikas rindas grafisko attēlu, redzam lauzītu līniju, kas atspoguļo parādības nevienmērīgas izmaiņas dažādos ar dinamikas rindu aptvertajos laika periodos. Izmaiņu nevienmērību cēlonis parasti ir dažādi faktori ar īslaicīgu darbību, kuriem bieži ir gadījuma raksturs. No zinātniskā un praktiskā viedokļa vislielāko interesi izraisa izmaiņu pamattendence, retāk jāpētī īslaicīgas gadījuma rakstura novirzes no šīs tendences.

Lai no dinamikas rindas izslēgtu gadījuma novirzes un atklātu tās pamattendenci, rindu izlīdzina. Daļēji to veic, izmantojot jau minētos slīdošos vidējos. Pilnīgāk šo uzdevumu atrisina, izdarot analītisko izlīdzināšanu.

Dinamikas rindas analītiskā izlīdzināšana, izmantojot ģeometrisku ilustrāciju, nozīmē, ka tās lauzītās līnijas vietā, kura attēlo dinamikas rindu, tiek novilkta taisne vai vienmērīgi izliekta līkne, kas atrodas ''vistuvāk'' minētajai lauzītajai līnijai. Matemātiski tāds uzdevums nozīmē atrast izlīdzinātās taisnes vai līknes vienādojumu, resp., vienādojuma parametrus.

Analītisko izlīdzināšanu parasti izdara ar vismazāko kvadrātu metodi, tādēļ aprēķini ir līdzīgi kā nosakot regresijas vienādojumu regresijas un korelācijas analīzē. Dažos gadījumos šo darbu ir iespējams vienkāršot.

Analītiskā izlīdzināšana, tās rezultātu novērtēšana un elementārais pielietojums aptver šādus secīgi izpildāmus uzdevumus.

 

1. Izlīdzinošās taisnes vai līknes pamatojumu, resp., sakarību veida izvēli.

 

2. Taisnes vai līknes parametru aprēķināšanu.

 

3. Teorētisko jeb izlīdzināto rindas līmeņu aprēķināšanu, vajadzības gadījumā izdarot interpolāciju un ekstrapolāciju, ja tā ir pamatota.

 

4. Izlīdzināšanas kvalitātes novērtēšanu, atrodot dažādus sakarību ciešuma rādītājus.

 

Dinamikas rindu izlīdzinošo taisni vai līkni, resp., tās vienādojumu ir pieņemts saukt par trendu (trenda vienādojumu, pamattendences modeli).

 

 

14.2.2.Trenda veida pamatojums

 

Izlīdzinošās līnijas (taisne, līkne) vispārīgo veidu nosaka, veicot dinamikas rindas iepriekšēju novērtēšanu, ekspertīzi. Ir daži matemātiski paņēmieni, kas šo procesu var atvieglot, bet tos nedrīkst lietot formāli. Vienkāršākie paņēmieni ir šādi.

 

1.  Izmaiņu tendences kvalitatīvās dabas izpēte.

 

Ja dinamikas rindai visos periodos ir aptuveni vienādi absolūtie pieaugumi, parādība izmainās atbilstoši aritmētiskai progresijai, tad to var aprakstīt ar taisni, atrodot lineāru vienādojumu.

Ja dinamikas rindai visos periodos ir aptuveni vienādi pieauguma tempi, tad parādība izmainās atbilstoši ģeometriskajai progresijai. To var modelēt ar pakāpes vienādojumu, kuru linearizē, izmantojot logaritmus.

Ja parādība attīstās lavīnveidā, to samērā labi modelē eksponentfunkcija.

 

2.  Ja parādības pamattendenci nevar noskaidrot iepriekš minētajā veidā, tad izgatavo dinamikas rindas grafisko attēlu un novērtē, kādas samērā vienkāršas funkcijas grafiskajam attēlam vislabāk atbilst lauzītā līnija. Ja arī tādā veidā pamatota izvēle nav iespējama, no vienlīdz šķietami pamatotām sakarību formām izvēlas vienkāršāko, bieži lineāru sakarību. Jo sakarību veids ir vienkāršāks, jo retāk tiek pieļautas rupjas kļūdas, izdarot rindas ekstrapolāciju, kas nepieciešams prognozēšanā.

Praksē, izdarot dinamikas pamattendences ekspertīzi, bieži jāsastopas ar tādām dinamikas rindām, kuras aptver divus vai vairākus periodus ar atšķirīgām izmaiņu tendencēm.

 

14.3. tabulā un 14.2. grafiskajā attēlā ir parādīta dzimstības koeficienta (dzimušo bērnu skaita, rēķinot uz1000 iedzīvotājiem) dinamika 1978.-1995.g. Lauzītā līnija ir tuva līknei ar maksimumu 1986.-1987.g. Dažos mācību līdzekļos ir sastopami ieteikumi šādu dinamiku modelēt ar kādu funkciju, kurai ir ekstrēms, piemēram, ar otrās kārtas parabolu. Tāda rīcība parasti nav pamatota, īpaši tad, ja trenda modeli grib izmantot ekstrapolācijai, izstrādājot statistisku prognozi. Piemēra ietvaros neliels dzimstības koeficienta pieaugums 1978.-1986.g. periodā nav uzlūkojams ne par cēloni, ne pamatojumu, lai prognozētu virsproporcionālu šī koeficienta samazināšanos sekojošā 1987.-1995.g. periodā un turpmāk.

3.tabula

Latvijā dzimušo bērnu skaits, rēķinot uz 1000 iedzīvotājiem gadā

(dzimstības koeficients)

 

Gads

1978

1979

1980

1981

1982

1983

1984

1985

1986

1987

1988

1989

1990

1991

1992

1993

1994

1995

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Laika

arguments t

1

2

3

4

5

6

7

8

 

9

1

 

2

 

3

 

4

 

5

 

6

 

7

 

8

 

9

 

10

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Dzimuši

13,7

13,8

14,1

14,2

14,8

15,9

15,9

15,4

16,1

16,0

15,6

14,6

14,2

13,0

12,0

10,3

9,5

8,6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Datu avots: Latvijas demogrāfijas gadagrāmata, 1996. - 39.,40. lpp.

 

Ja dinamikas rindas vidū ir vērojami ekstremāli līmeņi, aplūkojamā periodā parasti ir darbojušās divas atšķirīgas izmaiņu tendences, kuras ir jāizlīdzina un jāmodelē katra atsevišķi.

Piemērā 1978-1986.g. periodā dzimstības koeficients ir audzis, bet sekojošā 1987.-1995.g. periodā - samazinājies. Pirmajā tuvinājumā abas tendences var modelēt ar lineāru trendu (taisni).

 

 

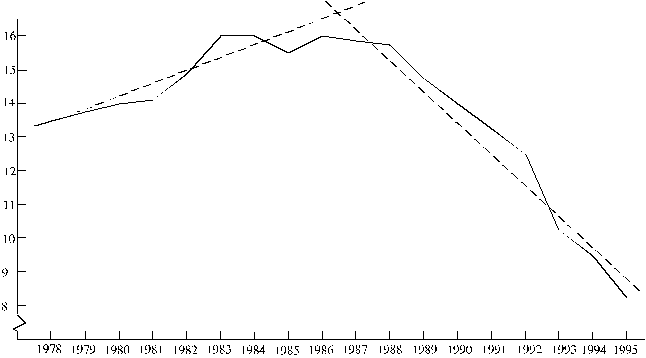
14.2. attēls  Latvijā dzimušo bērnu skaits, rēķinot uz 1000 iedzīvotājiem

(dzimstības koeficients)

 

 

14.2.3. Taisnes vienādojuma atrašana

 

Lai atrastu lineāra trenda (taisnes)    vienādojumu, par neatkarīgo mainīgo lielumu t pieņem  rindas līmeņu secības numurus, kurus sauc arī par līmeņu secības koeficientiem vai laika argumentiem, bet par atkarīgo mainīgo lielumu y - pašus rindas līmeņus.

Rindas līmeņu secības koeficientu t var izraudzīties dažādi. Var ņemt parastos gadskaitļus (piemēra pirmajā daļā 1978.,1979., ..., 1986.), bet, tā kā tie ir lieli skaitļi, tad nepamatoti tiek palielināts skaitļošanas apjoms. Ērtāk par līmeņu secības koeficientiem izraudzīties dabisko skaitļu rindas pirmos skaitļus (piemērā 1,2,...,9). Abos gadījumos taisnes parametru atrašanai ir jāsastāda un jāatrisina normālvienādojumu sistēma

 

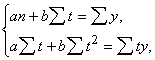                                                                                                         (14.10)

 

kas formāli ne ar ko neatšķiras no sistēmas, kuru izmanto regresijas vienādojuma atrašanai.

 

Ja darbu izpilda ar vienkāršu (neprogrammējamu) skaitļotāju, aprēķinus var tālāk vienkāršot, līmeņu secības numurus centrējot. Ja rindā ir nepāra skaits līmeņu, tad centrālajam līmenim piešķir numuru 0, pirms tā esošajiem līmeņiem ''numurus''-    -1, -2 utt., bet sekojošiem līmeņiem 1, 2 utt. Šādā gadījumā   un normālvienādojuma sistēma (14.10) ir vienkāršāka:

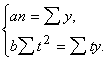                                                                                                                     (14.11)

 

 

No sistēmas (14.11) atrodam, ka                                    

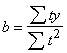                                                       '                                                       (14.12)

 

Mūsdienās trendu modeļu paramertus parasti aprēķina vai nu ar datoru, vai ar programmētas vadības kalkulatoru. Ir programmas, kas laika argumentus dabisko skaitļu rindas veidā (1,2,3,...) formē automātiski. Tad skaitļotājā secīgi jāievada vienīgi rindas līmeņi.

Šādi apstrādājot 14.3. tabulā un 14.2. attēlā dotās dinamikas rindas divas daļas ar atšķirīgām izmaiņu tendencēm, iegūstam divus lineārus trendus:

 

                                      (pirmajam periodam) un

                                    (otrajam periodam).               

 

Aprēķinos iegūtās kosummas kā strarprezultāti parādītas 14.4. tabulā, no kurām viegli   sastādīt normālvienādojumu sistēmu, ja rodas tāda vajadzība, un izdarīt citus aprēķinus. Piemēra otrajam periodam:   

 

                                                                                               

 

                                                                                  14.4.tabula

Analītiskās izlīdzināšanas krossummas, 

trenda taisnes parametri un korelācijas koeficients

 

 

1. perioda taisne

2. perioda taisne

n

9

            10

            45

            55

           285

           385

133.9

129.9

 1999.61

 1756.67

  689.2

  640.2

b

          0.3283

       - 0.9000

a

     13.24

     17.94

r

        0.930

      - 0.982

 

Lineāra trenda koeficientu interpretē samērā līdzīgi kā regresijas vienādojuma koeficientu. Trenda koeficients rāda, par cik vienībām vidēji vienā laika vienībā pieaug (samazinās) dinamikas rindas līmenis.

Piemēra pirmajā periodā dzimstības koeficients pieaug vidēji par 0,328 gadā, resp. par 0,328 bērniem, rēķinot uz 1000 iedzīvotājiem, bet otrajā periodā -- samazinās vidēji par 0,900 gadā.

Trenda vienādojuma brīvajam loceklim, tāpat kā regresijas vienādojuma brīvajam loceklim, interpretācijas iespējas ir ierobežotas.

Rindas izlīdzinātos līmeņus atrod, ievietojot šajā vienādojumā līmeņu secības numurus. Piemēram, aplūkotās dinamikas rindas otrajā daļā 1995. gadam atbilst t=10. Ievietojot to trenda modelī   iegūstam:

 

 (faktiskais rindas līmenis 8,6).

 

Ja izlīdzināto rindas līmeni grib pagarināt, nosaka turpmākiem gadiem atbilstošos laika argumentus. Piemēram, 1998. gadam atbilst t =13 un  Vai šo skaitli drīkst uzlūkot par prognozi, ir atkarīgs no tā, kāds ir ekspertīzes vērtējums, vai modeļa izteiktā tendence saglabāsies, vai mainīsies.

Piemēra ietvaros formāli var izskaitļot gadu, kad dzimstības koeficients kļūs nulle.

Vadoties pēc otrā perioda lineārā trenda, tas notiks, kad  , resp. 2005 gadā. Pēc tam dzimstības koeficienta prognoze iznāk negatīva, kas nevar būt. Reāli tas nav iespējams. Tādēļ visticamāk, ka turpmākos gados atkal šī koeficienta izmaiņu likumsakarība mainīsies. Ja arī koeficients nesāks augt, tas varētu stabilizēties kādā fiksētā līmenī ar ļoti mazu (pozitīvu vai negatīvu) izmaiņu tendenci.

 

Aprēķinot trenda taisni, pie visiem līmeņu secības numuriem (laika argumentiem) var  pieskaitīt vai no tiem atņemt konstantu lielumu, būtiski neizmainot iegūstāmos rezultātus. Šādā gadījumā izmainās vienīgi trenda vienādojuma brīvais loceklis, bet tā koeficients, kā arī izlīdzinātās rindas līmeņi nemainās.

Aprēķinot trenda modeli līknes formā, līmeņu secības numurēšanas sistēma ir jāpamato rūpīgāk, jo daudzos gadījumos tā ietekmē visus izlīdzināšanas rezultātus. Līmeņu secības numurēšanas sistēma rezultātus ietekmē sevišķi uzskatāmi, ja izlīdzināšanai izmanto pakāpes modeli, kuru linearizē logaritmējot.

 

 

14.2.4. Izlīdzināšanas  kvalitātes  novērtēšana

 

Kad izlīdzinošā līnija (trenda vienādojums) ir noteikta, jānovērtē, vai tā izsaka tendenci, kas atbilst profesionālam priešstatam par parādības izmaiņām aplūkojamā periodā un iepējamām izmaiņām nākotnē.

Piemēra otrajā periodā taisne diezgan labi izsaka dzimstības koeficienta izmaiņu pamattenenci. Tomēr, aplūkojot 2. attēlu, redzam, ka rindas centrālajā daļā faktiskie līmeņi atrodas virs izlīdzinātajiem, bet perioda sākuma un beigu gados - otrādi.

No formālā viedokļa raugoties, faktiskos datus labāk nekā taisne izlīdzinātu augšup izliekta līkne. Taču, izmantojot šādu līkni prognozēšanai, vēl ātrāk nekā ar taisni mēs iegūtu tik mazus dzimstības koeficientus, kādi reāli nav domājami.

No prognozēšanas viedokļa loģiski pieņemamāks trenda modelis būtu lejup izliekta līkne, piemēram, hiperbola, kas ekstrapolācijas apgabalā tuvotos kādam konstantam līmenim. Diemžēl faktiskie dati šādam pieņēmumam neatbilst.

Ja aprēķinātais analītiskais trends atbilst parādības izmaiņu vispārīgajam  kvalitatīvajam raksturam, var aprēķināt kvantitatīvus rādītājus, kā rindas izlīdzinātie līmeņi atbilst faktiskajiem līmeņiem. Šajā nolūkā aprēķina nosauktus (ar vienībām saistītus) un nenosauktus sakarību ciešuma rādītājus, kuri formāli līdzīgi tiem, kurus lieto regresijas un korelācijas analīzē.

 

Vispirms aprēķina faktiskās un izlīdzinātās dinamikas rindu līmeņu noviržu dispersiju.

 

                                                                                                              (14.13)

kur   -- rindas faktiskais līmenis  i- tajā periodā;

        -- izlīdzinātās rindas līmenis tajā pašā periodā;

         n --  rindas līmeņu skaits.

 

Ja dinamikas rinda ir samērā gara un visiem tās periodiem izlīdzinātie līmeņi netiek aprēķināti, lineāra trenda gadījumā var izmantot pārveidotu formulu

                                   

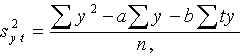                                  ,                                                (14.14)

kurā, tāpat kā formulā (14.13) , summēts tiek pa visu dinamikas rindu.

 

Konkrētajā gadījumā vieglāk izmantot formulu (14.14), jo mums 14.3.tabulā ir fiksētas vajadzīgās krossummas.

 

Piemēra otrajam periodam

 

                    .

 

Lietojot formulu (14.14), ir jāizmanto lielāks zīmīgo ciparu skaits, jo, izpildot atņemšanas darbības, formulas skaitītājā  daudzi zīmīgie cipari zūd. Tādēļ iegūtais rezultāts var būt diezgan neprecīzs.

Dinamikas rindas savstarpējo noviržu dispersijai nav vienības ar reālu saturu. Tādēļ par noviržu absolūtā lieluma mēru lieto noviržu standartnovirzi jeb vidējo kvadrātisko novirzi, kuru aprēķina kā kvadrātsakni no tikko aplūkotās dispersijas vai arī lietojot formulu

 

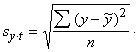                                                                                                             (14.15)

 

 

Piemērā                   

 

Dinamikas rindu savstarpējo noviržu standartnovirze ir izteikta rindas līmeņu vienībās un raksturo gadījuma faktoru izraisīto faktisko rindas līmeņu noviržu no izlīdzinātajiem līmeņiem vidējo.

Par izlīdzināšanas kvalitātes relatīvu (beznosaukuma) rādītāju izmanto ar trendu izskaidrotās dispersijas un rindas līmeņu kopējās dispersijas atiecību. Tā kā parasti aprēķina neizskaidroto dispersiju (14.13) , tad izskaidroto dispersiju atrod kā kopējās un neizskaidrotās dispersijas starpību. Minēto dispersiju attiecību līdzīgi kā regresijas analīzē sauc par determinācijas attiecību:

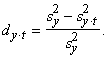                                                                                                                        (14.16)

Piemērā

                                      

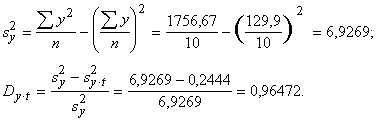
Apmēram 96% no rindas līmeņu dispersijas (svārstības  ap rindas aritmētisko vidējo) izskaidro lineārs parādības izmaiņu trends. Tā tad izlīdzināšanas kvalitāte ir ļoti laba.

Aprēķinot kvadrātsakni no determinācijas attiecības (14.16), iegūst rindas līmeņu un laika argumenta korelācijas indeksu, lineāra trenda gadījumā - korelācijas koeficientu.

                                 

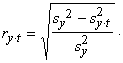                                                                                                                 (14.17)

 

Piemērā     kas norāda, ka sakarība ir ļoti cieša.      

 

Lineāra trenda gadījumā šo korelācijas koeficientu var aprēķināt arī tieši pēc krossummām:

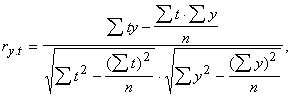                                   (14.18)

 

 

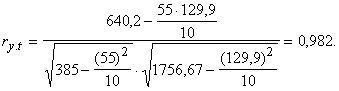
Arī korelācijas koeficienta aprēķināšana parasti ietilpst lietojamā tipveida programmā, un korelācijas koeficientu aprēķina bez tikko parādītajiem rakstiskajiem ievietojumiem formulā.

Rindas līmeņu un līmeņu secības numuru korelācijas koeficients lineāra trenda gadījumā nemainās, ja līmeņu secības koeficientiem pieskaita (no tiem atņem) konstantu lielumu. Tādēļ tādu pašu korelācijas koeficientu iegūstam, par līmeņu secības numuriem ņemot parastos gadskaitļus vai dabiskās skaitļu rindas skaitļus 1, 2, ...,n.

Izmantojot korelācijas koeficientu kā sakarību ciešuma rādītāju dinamikas rindu analīzē, jāievēro, ka tas ir atkarīgs arī no līmeņu secības numuru dispersijas, kura savukārt sistemātiski mainās, izmainot rindas garumu. Tādēļ dažāda garuma dinamikas rindām aprēķināti korelācijas koeficienti ir salīdzināmi tikai tuvināti.

Bieži gan zinātnē, gan praksē, novērtējot dinamikas rindas izlīdzināšanas kvalitāti un ekstrapolācijas rezultātā iegūto prognožu vērtējuma apgabalus, izmanto rādītājus, kurus aprēķina pēc  izlases kļūdu formulām . Tās ir analogas ar formulām, kuras lieto izlases kļūdu vērtēšanā regresijas analīzē. Matemātiska pamatojuma, kurš izrietētu no izlases metodes pamatteorēmām, šādai rīcībai nav, jo dinamikas rinda nav izlase matemātiskā nozīmē un no prognozējamā perioda vispār nekādu izlasi nevar iegūt. Ja tomēr minēto rādītāju aprēķināšana un lietošana praksē attaisnojas, tad tiem ir jāpiešķir cits loģiskais saturs. Izlases kļūdas un vērtējuma apgabali ir jāuzskata par dinamikas rindas svārstību rādītājiem un, attiecinot tos uz prognozējamo periodu, vienmēr jāpatur prātā pamathipotēze par trenda un svārstību stabilitāti  (inerci) , kas saskaņā ar hipotēzi saglabājās arī nākotnē. Tikai tad, ja šī hipotēze apstiprinās, ir pamats cerēt, ka attaisnosies aprēķinātie vērtējuma apgabali un ar tiem saistītās varbūtības.   

14.3. Sezonalitātes  pētīšana

 

14.3.1. Vienkāršākie sezonalitātes rādītāji

 

Par sezonālām svārstībām sauc dinamikas rindas līmeņu svārstības  kalendāra gada ietvaros, kuras ar lielāku vai mazāku regularitāti atkārtojas ik gadu. Sezonālās svārstības ir raksturīgas lauksaimnieciskai ražošanai, dažādu preču pieprasījumam un patēriņam, demogrāfiskiem procesiem utt. Lai pētītu sezonālās svārstības, ir jābūt statistiskiem datiem (dinamikas rindas līmeņiem)  par katru mēnesi atsevišķi vairāku gadu ilgā periodā. Dažos gadījumos var būt vajadzīgi dati pa nedēļām  vai pat pa dienām.

14.5. tabulā ir apkopoti dati par piena izslaukumu pa mēnešiem Latvijas lauksaimniecības uzņēmumos 11 gadu ilgā periodā. Lai sāktu pētīt izslaukuma sezonalitāti, vispirms ir jānoskaidro, vai parādībai piemīt ilgtermiņa izmaiņu tendence. 14.5. tabulas pēdējo divu aiļu dati rāda, ka vispārīgais izslaukuma līmenis šajā laika periodā izmainījies maz. Tādā gadījumā paši rindas līmeņi ir savā starpā salīdzināmi un dod labu priekšstatu par parādības sezonālo raksturu. Redzam, ka vislielākais piena izslaukums ir vasaras mēnešos (jūnijā, augustā), vismazākais ziemas mēnešos (novembrī - februārī). Tāda īpatnība saglabājas visā laika periodā.

Ja parādībai ir ilgtermiņa izmaiņu tendence, dažādu gadu mēnešu līmeņi nav tieši salīdzināmi. Tādā gadījumā ir jāaprēķina sezonalitātes relatīvie vai noviržu rādītāji. Šos rādītājus ieteicams aprēķināt arī tad, ja ilgtermiņa izmaiņu tendences nav vai tā ir neliela, jo relatīvie sezonalitātes rādītāji ir labāk salīdzināmi un tādēļ uzskatāmāki.

Visbiežāk lietotie sezonalitātes rādītāji ir sezonalitātes indeksi. Tos aprēķina, dalot konkrēto mēneša līmeni ar vidējo mēneša līmeni gadā. Piemēram, izslaukuma sezonalitātes indeks 11. gada janvārī ir 0,73 jeb 73 % ( 167 : 229 = 0,73 ). Vidējais sezonalitātes indekss ir 1, resp., 100 %, bet indeksu summa gada ietvaros ir 12 ( resp., 1200, ja saskaita procentu skaitļus ). Šī īpašība izpildās precīzi, ja vidējo mēneša līmeni ( izslaukumu ) aprēķina kā nesvērto vidējo, piemēram, 11. gadam    (167+162+...+151 ) : 12 = 228,8. Ja to pašu rādītāju aprēķina, dalot gada līmeni ( izslaukumu ) ar 12, var rasties neliela nesakritība, piemēram, 2753 : 12 = 229,4. Tas ir izskaidrojams ar dažām īpatnībām gada un mēneša līmeņu aprēķinos. Tomēr šī nesakritība parasti ir tik maza, ka nevar manāmi ietekmēt sezonalitātes rādītājus. Sezonalitātes indekss rāda, cik procentus veido konkrētā mēneša līmenis pret mēneša vidējo līmeni. Piemēram, 11. gada janvārī  izslaukums ir 73 %, bet jūnijā - 146 % no vidējā izslaukuma mēnesī.

14.5. tabula

 

Piena izslaukums vidēji no vienas govs Latvijas lauksaimniecības uzņēmumos , kg

 

Gads

Mēnesis

Gadā

Vidēji

 

I

II

III

IV

V

VI

VII

VIII

IX

X

XI

XII

 

mēnesī

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

158

145

185

218

273

341

351

324

275

225

167

168

2844

236

2

159

144

186

221

274

339

350

324

274

224

174

175

2855

237

3

166

161

204

235

281

339

341

327

270

203

141

144

2815

234

4

144

140

184

213

273

331

333

331

275

218

172

172

2790

232

5

173

166

209

228

270

335

342

321

283

222

168

169

2892

240

6

174

168

215

238

305

338

327

311

258

210

162

164

2859

239

7

169

170

216

239

281

337

346

322

268

217

188

192

2952

245

8

191

185

239

267

324

359

364

334

281

232

187

183

3151

262

9

187

177

229

250

288

341

343

322

257

200

160

152

2914

242

10

155

154

199

224

272

323

33o

313

266

220

165

166

2795

232

11

167

162

200

223

277

333

333

312

251

196

141

151

2753

229

Vidēji

168

161

206

232

283

338

342

322

269

215

166

167

2875

239

Ja parādībai nav izteiktas ilgtermiņa izmaiņu tendences un arī sezonalitāte nav izmainījusies būtiski, kā tas ir aplūkojamā piemērā, var aprēķināt visa laika perioda  vidējos sezonalitātes indeksus . Tos aprēķina tāpat kā atsevišķu gadu indeksus, tikai par sākotnējo informāciju izmanto visa laika perioda vidējos līmeņus ( 14.5. tabulas pēdējā rinda ). Piemēram, janvārī indekss ir
168 : 239 = 0,703  70 %. Piena izslaukuma sezonalitātes indeksi ir parādīti 14.6. tabulā.

14.6. tabula

Piena izslaukuma sezonalitātes indeksi, %

 

Gads

Mēnesis

 

I

II

III

IV

V

VI

VII

VIII

IX

X

XI

XII

 

 

 

 

 

 

 

 

 

 

 

 

 

1

67

61

78

92

116

145

149

137

117

95

71

71

2

67

61

78

93

116

143

148

137

116

95

73

74

3

71

69

87

100

120

145

146

14o

115

87

60

61

4

62

6o

79

92

118

143

144

143

118

94

74

74

5

72

69

87

95

112

140

142

134

118

92

70

70

6

73

70

90

99

128

141

137

130

108

88

68

69

7

69

69

88

98

115

137

141

131

109

89

77

78

8

73

71

91

102

124

137

139

127

107

89

71

70

9

77

73

95

103

119

141

142

133

106

83

66

63

10

67

66

86

96

117

139

142

135

115

95

71

71

11

73

71

87

97

121

146

146

136

110

86

62

66

Vidēji

70

67

86

97

118

141

143

135

113

90

69

70

 

Ja sezonalitāti pētī kā ekonomisku parādību, tad analīzi veic pa reāliem kalendāra mēnešiem, kā to parādījām piemērā, jo kalendāra mēneši ir vispār pieņemti uzskaites, pārskata un plānošanas periodi. Turpretī, pētījot sezonalitāti kā dabas vai bioloģisku parādību, ir lietderīgi izslēgt mēnešu atšķirīgā ilguma ietekmi. Šajā nolūkā sākotnējos rindas līmeņus pārrēķina atbilstoši vienāda, nosacītā ilguma mēnešiem  (parasti 30,5 dienas). Piemēram, izslaukums 11. gada nosacītajā februāra mēnesī ir , bet sezonalitātes indekss

Visa sezonalitātes indeksu rinda 11. gada nosacītajos mēnešos ir šāda: 71,8; 74,4; 85,6; 98,6; 119,0; 148,4; 143,6; 133,8; 111,8; 84,6; 63,0; 64,9 (%). Šī indeksu rinda ir daudz vienmērīgāka un veido samērā pareizu vilni ar minimumu decembrī, bet maksimumu jūnijā. Turpretī kalendāra mēnešu sezonalitātes indeksi izslaukuma  minimumu uzrāda novembrī, un arī februārī izslaukums ir mazāks nekā abos blakus esošajos mēnešos (sk. 14.6. tabulu).

Analizējot intervālu dinamikas rindu, kuras mēneša līmeņus var summēt, iegūstot gada līmeni, parādības sezonalitāti  var raksturot arī ar  struktūras relatīvajiem lielumiem . Turpinot piemēru, var aprēķināt katra mēneša  īptsvaru, visa gada izslaukumu pieņemot par 100. Piemēram, 11. gada janvārī iegūts 167 : 2753 = 0,6066   6,1 %  no gada izslaukuma. Ja sezonalitātes nebūtu, struktūras relatīvie lielumi visos mēnešos būtu 1: 12 = 0,0833  8,3 %; šo skaitli var izlietot faktiski iegūto lielumu novērtēšanai.

 

 

14.3.2. Sezonalitātes  izmaiņu  pētīšana

 

Laika gaitā var izmainīties ne tikai dinamikas rindas vispārējais (gada) līmenis, bet arī sezonalitātes īpatnības: sezonalitāte var samazināties vai palielināties, var pārvietoties no viena mēneša uz otru sezonalitātes maksimums un minimums  utt.

Sezonalitātes palielināšanos vai samazināšanos, neatklājot citu īpatnību izmaiņas, var konstatēt, aprēķinot katram gadam atsevišķi  sezonalitātes indeksu svārstību rādītājus , piemēram, standartnovirzi. Ja sezonalitātes  indeksi ir izteikti procentos, indeksu standartnovirzi aprēķina pēc formulas

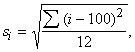                                                                                                              (14.19)

 kur i - sezonalitātes indekss kārtējā mēnesī; summēšana jāizdara pa gada visiem 12 mēnešiem.

 

Ja indeksu standartnovirzes no gada gadā pieaug, tad parādības sezonālais raksturs palielinās un otrādi - ja indeksu standartnovirzes no gada gadā samazinās, tad samazinās parādības sezonālais raksturs

Lai sezonalitātes izmaiņas izpētītu detalizētāk, katra mēneša sezonalitātes rādītāji ir jāuzskata par patstāvīgu dinamikas rindu un jāapstrādā, izmantojot iepriekš aplūkotās metodes. Piemēram, šos rādītājus var izlīdzināt analītiski ar vismazāko kvadrātu metodi.

Lai sezonalitātes rādītāju trendi būtu vienkāršāki, analītiskai izlīdzināšanai sezonalitātes indeksu vietā ieteicamāk lietot  sezonalitātes novirzes. Novirzes kā absolūti lielumi parasti izmainās pēc aritmētiskās progresijas likuma, tādēļ var izmantot lineāru trenda modeli. Indeksi kā relatīvie lielumi visbiežāk izmainās pēc ģeometriskās progresijas likuma, un tāpēc jālieto sarežģītāks modelis.

Sezonalitātes novirzes aprēķina, atņemot no konkrētajiem mēnešu līmeņiem attiecīgā gada vidējo mēneša līmeni. Piemēram, 11. gada janvārī vidējais izslaukums no vienas govs ir bijis par 62 kg mazāks nekā vidēji caurmērā mēnesī  ( 167 - 229 = -62 (kg). Šādu noviržu dinamikas rindas ir parādītas 7. tabulā.

 

 

 

 

 

 

 

14.7. tabula

Vidējā piena izslaukuma no vienas govs mēnešu novirzes  no mēnešu vidējā izslaukuma

 

Gads

Mēnesis

 

I

II

III

IV

V

VI

VII

VIII

IX

X

XI

XII

 

 

 

 

 

 

 

 

 

 

 

 

 

1

-78

-91

-51

-18

37

105

115

88

39

-11

-69

-68

2

-78

-93

-51

-16

37

102

113

87

37

-13

-63

-62

3

-68

-73

-30

   1

47

105

107

93

36

-31

-93

-90

4

-88

-92

-48

-19

40

99

101

99

43

-14

-60

-60

5

-68

-74

-32

-12

30

94

102

80

42

-18

-72

-72

6

-65

-71

-24

  -1

66

99

  88

72

19

-29

-77

-75

7

-76

-75

-29

  -6

36

92

101

77

23

-28

-57

-53

8

-71

-77

-23

  5

62

97

102

72

19

-30

-75

-79

9

-55

-65

-13

  8

46

99

101

80

15

-42

-82

-90

10

-77

-78

-33

 -8

40

91

  98

81

34

-12

-67

-66

11

-62

-66

-28

-6

48

104

104

83

22

-33

-88

-78

 

Uzskatot 14.7. tabulas katru kolonnu par patstāvīgu dinamikas rindu, var aprēķināt šīs rindas vidējo līmeni   dispersiju   standartnovirzi   un variācijas koeficientu   izmantojot parastās formulas. Šādi rādītāji sakopoti 14.8. tabulas pirmajā daļā. Tālāk katram mēnesim  var aprēķināt lineāru trendu

 kur  izslaukuma novirze no vidējā mēneša laikā; t - laika arguments (piemērā t =1, 2, ... , 11 ). Trendu aprēķina, izmantojot parastās formulas, kas aplūkotas iepriekš.

Novērtējot iegūto trendu statistisko nozīmību, jāatzīmē, ka nelielam brīvības pakāpju skaitam (v = 9) tā ir zema. Tādēļ noskaidrotās sezonalitātes izmaiņas var būt arī gadījuma cēloņu sekas. Tomēr vispārēju priekšstatu no tām gūstam.

Ievietojot atrastajos trendu vienādojumos aplūkotā perioda pirmā un pēdējā gadu līmeņu secības koeficientus  iegūstam izlīdzinātās novirzes dinamikas rindas sākumā un beigās (14.8. tabulas 7. un 8. rinda). Pieskaitot šīs novirzes pie attiecīgo gadu vidējiem mēnešu izslaukumiem, iegūstam izlīdzinātos  izslaukumus pa mēnešiem ( 14.8.tabulas 9. un 10. rinda ). Tālāk parastajā veidā aprēķina izlīdzināto izslaukumu pa mēnešiem sezonalitātes indeksus  procentos (14.8. tabulas 11. un 12. rinda). Labākas uzskatāmības dēļ divu pēdējo rindu datus var attēlot ar radiagrammu, kā parādīts 14.3. attēlā.

 

 

 

 

 

14.8. tabula

 Izslaukuma sezonalitātes izmaiņu svarīgākie rādītāji

 

Rādītāji

Gads

Mēnesis

 

 

I

II

III

IV

V

VI

VII

VIII

IX

X

XI

XII

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Vidējā novirze

       , kg

_

  -71

  -77

   -33

     -7

44

99

103

83

30

-24

-73

-72

2. Noviržu standart-

    novirze   ,  kg

_

8.7       

 9.6

    11.7

 8.7

10.6

4.7

6.9

8.0

9.9

10.0

10.9

11.3

3. Variācijas koefi-

     cients,  %

_

   12

    12

    36

  134

 24

    5

    7

  10

  33

  42

  15

  16

4. Lineārā trenda

     koeficients  b

_

   1.36

   2.16

   2.64

   1.52

    1.04

   -0.66

   -1.2

   -1.32

   -2.06

   -1.65

   -0.84

   -0.77

5. Lineārā trenda

     brīvais loceklis a

_

   -80

   -91

   -49

   -16

  38

103

110

  91

  42

 -14

 -68

 -67

6. Korelācijas

     koeficients  r

_

0.491

0.717

0.715

0.549

0.311

-0.442

-0.549

-0.524

-0.660

-0.520

-0.246

-0.217

Ar trendu izlīdzinātās
 novirzes

 

 

7. t = 1

1

    -78

    -88

    -46

   -14

39

102

109

  90

  40

-16

-69

-68

8. t = 11

11

    -65

    -67

    -20

       1

49

 95

 97

 76

 19

-32

-77

-76

Izlīdzinātie izslaukumi
 pa mēnešiem,
 kg :

 

 

9.

1

    159

    149

    191

   223

276

339

 346

326

277

221

168

169

10.

11

    164

    162

    210

   230

279

325

 326

306

249

197

152

153

Izlīdzināto izslaukumu
 pa mēnešiem sezona-
 litātes indeksi , % :

 

 

11.

1

      67

     63

      80

    94

117

143

146

138

117

93

71

71

12.

11

      72

     71

      91

  100

122

142

142

133

108

86

66

67

 

 

 

 

 

 

 

 

 

 

 

 

 

 

- - - -     1. gads   ______      11. gads

 

14.3.attēls. Ar trendiem izlīdzinātie izslaukuma sezonalitātes indeksi

 

Izmantojot 14.8. tabulas datus un 14.3. attēlu, var izdarīt secinājumu, ka gada pirmajos mēnešos ( janvārī - aprīlī ) negatīvā izslaukuma sezonalitāte ir samazinājusies, bet aprīlī novērsta pavisam. Tāpat  samazinājusies pozitīvā sezonalitāte vasaras mēnešos ( jūnijā - septembrī ). Turpretī negatīvā sezonalitāte gada beigās ( oktobrī - decembrī ) ir palielinājusies.

 

 

14.3.3. Sezonalitātes viļņa modelēšana ar trigonometriskajām funkcijām

 

Risinot dažus analīzes un prognozēšanas uzdevumus, ir lietderīgi izlīdzināt dinamikas rindas  mēnešu līmeņu svārstības gada ietvaros. Izmantojot ģeometrisko ilustrāciju, tas nozīmē lauzīto līniju 14.3. attēlā aizstāt ar vienmērīgi izliektu līkni (attēlā ir divas šādas līnijas, katru no tām var izlīdzināt atsevišķi). Šādu izlīdzināšanu var izdarīt pēc viena vai vairāku gadu faktiskajiem datiem vai pēc    datiem, kuri vispirms izlīdzināti ar trenda modeļiem. Var izmantot gan kalendāra mēnešu, gan nosacīto mēnešu datus. Tomēr izlīdzināšana  ir pamatotāka, efektivāka un sasniedzama, lietojot vienkāršākus modeļus, ja izmanto pēc trendiem iepriekš izlīdzinātus līmeņus, pārrēķinot tos nosacītiem vienāda ilguma mēnešiem.

Ar trendiem izlīdzinātie, vienāda ilguma mēnešiem aprēķinātie izslaukuma sezonas indeksi 11. gadam ir parādīti 14.9. tabulas 2. ailē (indeksi izteikti skaitļa  1 daļās). Indeksus aprēķina, izmantojot 14.8. tabulas datus, piemēram, janvārim   indekss  ir     (229,2 ir vidējais mēneša izslaukums 11. gadā) .Šos indeksus (14.9. tabulas 2. aile) izmantojam par sākotnējo informāciju tālākai izlīdzināšanai ar trigonometrisko modeli.

Sezonas svārstību vilni modelē, izmantojot t.s.  harmonisko analīzi, kas pamatojas uz Furjē rindām. Par harmonisko analīzi sauc rindas

 

                                                       (14.20)

 

parametru (koeficientu)  aprēķināšanu. Argumentu  x ar dinamikas rindas līmeņu secības koeficientiem ( laika argumentiem)  t  saista sakarība

                                                                                                                              (14.21)

ja aprēķinus paredzēts veikt radiānos, vai sakarība

                                   

                                                                                                                             (14.22)

ja aprēķini tiks izdarīti grādos.

14.9.tabula

 

Sākotnējās informācijas sagatavošana sezonalitātes viļņa modelēšanai

un izlīdzināšanas rezultāti

 

Mēneši t

 

 

 

 

 

 

 

 

 

 

 

1

0.704

30

 0.5

 0.866

 0.3520

 0.6097

0.4956

0.25

0.75

0.628

2

0.743

60

 0.866

 0.5

 0.6434

 0.3715

0.5520

0.75

0.25

0.724

3

0.901

90

 1

 0

 0.9010

 0

0.8118

1

0

0.895

4

1.020

120

 0.866

-0.5

 0.8833

-0.5100

  1.0404

0.75

0.25

1.093

5

1.198

150

 0.5

-0.866

 0.5990

-1.0375

  1.4352

0.25

0.75

1.267

6

1.442

180

 0

-1

 0

-1.4420

  2.0794

0

1

1.369

7

1.399

210

-0.5

-0.866

-0.6995

-1.2115

  1.9572

0.25

0.75

1.372

8

1.314

240

-0.866

-0.5

-1.1379

-0.6570

  1.7266

0.75

0.25

1.276

9

1.105

270

-1

 0

-1.1050

 0

  1.2210

1

0

1.105

10

0.845

300

-0.866

 0.5

-0.7318

 0.4225

  0.7140

0.75

0.25

0.907

11

0.674

330

-0.5

 0.866

-0.3370

 0.5837

  0.4543

0.25

0.75

0.733

12

0.657

360

 0

 1

 0

 0.6570

  0.4316

0

1

0.631

12.003

X

 X

 X

-0.6325

-2.2136

12.9191

6

 6

 12.000

 

Laika arguments  t šajās formulās nozīmē mēnešus( t =1, 2, ............12), p  ir laika vienību skaits; analizējot sezonalitāti,  p ir  mēnešu skaits gadā, tātad p =12. Ņemot vērā šis norunas, formulas (14.21 un 14.22)  kļūst vienkāršākas:

 

                                      (radiānos)                                          (14.23)

vai                                            X =30t (grādos)                                                                       (14.24)

 

Modeļa (14.20) katrs loceklis , ,  utt. veido vienkāršu trigonometrisku vilni. Vairāku locekļu summa apvieno šos viļņus un izveidojas sarežģīta viļņveida līkne, kura var atspoguļot reālo parādības dinamiku.

Modeļa (14.20) daļu   sauc par  pirmo harmonisko komponenti, un tās vilnis aptver visu periodu (piemērā - gadu). Otrā harmoniskā komponente

  veido divas reizes īsāku vilni (piemērā šī viļņa garums ir seši mēneši) utt. Maksimāli var izdalīt p/ 2 (piemērā 12:2 =6) pilnas harmoniskās komponentes. Pēc modeļa, kurš satur pilnu skaitu harmonisko koponenšu, aprēķinātie jeb izlīdzinātie rindas līmeņi precīzi sakrīt ar faktiskajiem, tātad izlīdzināšana īstenībā vairs nenotiek. Tādēļ praksē aprēķina tikai dažas harmoniskās komponentes - tik daudz, kamēr aprēķinātā līkne atveido visas empīriskās līnijas galvenās īpatnības. Aproksimācijas (atbilstības) pakāpi var novērtēt ar dispersijas analīzi vai vienkāršāk - aprēķinot un novērtējot korelācijas indeksus kā jebkuram citam modelim, kurš izlīdzina dinamikas rindu.

Parametrus ,  aprēķina ar vismazāko kvadrātu metodi. Tā kā modeļa (14.20) locekļi ir ortogonāli  ( to savstarpējās korelācijas koeficienti ir nulles), var aprēķināt katru parametru atsevišķi, lietojot pāru analīzes tipveida algoritmu un programmu. Pēc tam aprēķinātos parametrus ievieto modelī (14.28).

Ja izmanto taustiņu skaitļošanas mašīnas, darbu var vienkāršot vēl tālāk, parametru  ,   aprēķināšanai izmantojot šādas formulas:

 

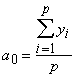                                                            ,                                                                (14.25)

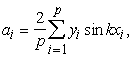                                                   (14.26)

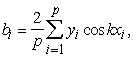                                                   (14.27)

 

kur  k - harmoniskās komponentes numurs ( piemērā  k - 1, 2, ... ,6).

 

Sākotnējās informācijas sagatavošana pirmās harmoniskās komponentes atrašanai ir parādīta 14.9. tabulā . Pēc šīs tabulas var datiem var aprēķināt, ka

 

                                          

                               

                             

Tādējādi izlīdzinošais vienādojums, kurš satur pirmo harmonisko komponenti ir šāds:

 

                                                                                  (14.28)

 

Tikai nedaudz darbietilpīgāka ir korelācijas un determinācijas indeksu aprēķināšana. Ievērojot modeļa (14.20) labās puses locekļu ortogonalitāti, arī korelācijas indeksus var aprēķināt katram loceklim atsevišķi, bet daudzfaktoru korelācijas indeksu atrast kā  kvadrātsakni no visu vienkāršo determinācijas indeksu summas.

Izdarot parastās ievietošanas korelācijas koeficienta formulā, atrodam, ka dinamikas rindas līmeņu un laika argumenta  trigonometrisko pārveidojumu korelācijas koeficientus var aprēķināt pēc formulām

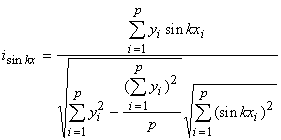 ,                                    (14.29)

 

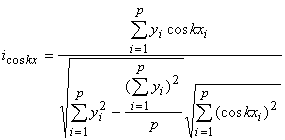  .                                  (14.30)

 

Lai lietotu šīs formulas, darba tabula 14.9. ir jāpapildina ar ailēm  8 - 10. Aprēķinot tālākās  harmoniskās komponentes, var ņemt vērā, ka daži aprēķinos jau izmantotie lielumi atkārtojas.

Bez tam var ievērot, ka  visiem  k, izņemot pēdējo  k  vērtību.

 

 

 

Turpinot piemēru, aprēķinām, ka

 

 ,                           

 

 

 ,                           

 

 

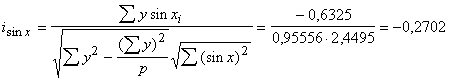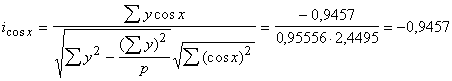Tā tad fomulas (14.28) pirmais loceklis izskaidro aptuveni 7 %, bet otrais loceklis - aptuveni 89 % no dinamikas rindas līmeņu dispersijas ( piemērā - no izslaukumu noviržu dispersijas).

Kopējo determinācijas indeksu aprēķina kā atsevišķo indeksu summu un kontrolē, kā šī summa tuvojas savai robežai - skaitlim 1. Piemērā  D = 0,0730+0,8944= 0,9674. Tātad pirmā harmoniskā komponente no izlīdzinātās rindas dispersijas izskaidro vairāk nekā 96 %, kas parasta uzdevuma ietvaros ir pilnīgi pietiekami. Attiecīgo korelācijas indeksu atrod kā kvadrātsakni no derminācijas indeksa :  Līdz ar to modeli (14.28) atzīstam par pabeigtu. Lai modelis būtu ērtāks izlīdzināto līmeņu aprēķināšanai ,  x vietā  ievieto tā vērtības no formulas (14.23), ja aprēķinus vēlamies veikt radiānos,  vai formulas (14.24), ja aprēķinus paredzēts izdarīt grādos. Tā kā vienkāršie skaitļotāji parasti trigonometriskās darbības izdara grādos, izmantojam variantu

                               

                                                                  (14.31)

kur  t  ir 1, ... , 12 (laika vienību secības numuri).

 

Izlīdzinātās izslaukumu novirzes, kuras aprēķinātas ar šo modeli, ir parādītas 14.9. tabulas pēdējā ailē. Praktiskos nolūkos no sezonalitātes indeksiem ir viegli pāriet atpakaļ uz izlīdzinātiem  rindas līmeņiem. Sākotnējie un izlīdzinātie sezonalitātes indeksi (procentos) parādīti 14.4. attēlā. Lai uzsvērtu, ka modelis (14.31) nav saistīts ar diskrētām  t  vērtībām, izlīdzinātajai rindai atbilstošie punkti ir savienoti ar līkni.

Sezonalitātes viļņa trigonometrisko modeli lieto interpolācijas uzdevumos, ja jānosaka izlīdzinātais parādības līmenis periodā, kas īsāks par vienu mēnesi, kā arī prognozēšanā.

 

 

 

 

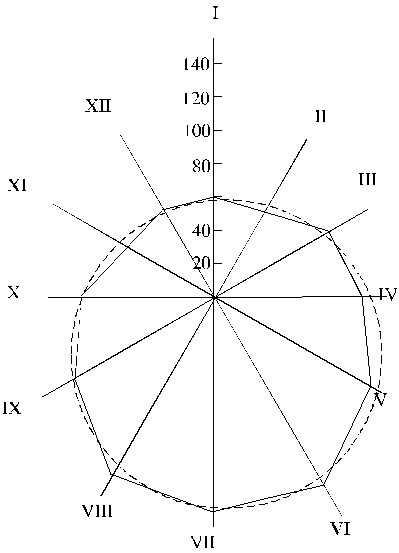
_______ sezonalitātes indeksi       - - - - - trigonometriskā līkne

 

14.4.att. Sezonalitātes indeksi un trigonometriskā līkne.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

14.4.  Vairākkomponentu  dinamikas  rindas modelēšana

 

14.4.1. Uzdevuma nostādne un lineāri trendi

 

Viens no ekonometrijas un statistikas pamatuzdevumiem ir atklāt un izpētīt dažādu parādību un procesu izmaiņas un šo izmaiņu tendences. Lielāko daļu statistikas datu sakārto dinamikas rindās. Tādēļ dinamikas rindu izpētei ir svarīga vieta statistikas teorijā un ekonometrijā.

Izpētot dinamikas rindas parasti cenšas izdalīt:

1)  izmaiņu pamattendenci jeb trendu; 2)  periodiskās svārstības, ja tādas ir; 3) sezonas svārstības, ja rindas līmeņi uzrādīti par gadu īsākos laika periodos vai momentos, un 4)  nejaušās novirzes jeb svārstības, kurām ir gadījuma raksturs. Bieži neizpēta visas uzrādītās dinamikas komponentes, bet tikai pirmo  vai pirmās, jo tās ir svarīgākās.

Dinamikas rindas modelēšanu ilustrēsim ar Latvijas lauksaimniecības uzņēmumos iegūtās graudaugu ražības dinamiku no 1950. līdz 1989.g.

Graudaugi ir Latvijas apstākļos vissvarīgākā zemkopības kultūra, un to ražībai vienmēr ir pievērsta prioritāra vērība gan zinātniskos pētījumos, gan lauksaimniecības praksē. Aptvertais laika periods - 40 gadi - ir pietiekami ilgs, lai varētu cerēt ieraudzīt un aprakstīt izmaiņu pamattendenci. Pagarināt šo periodu nav lietderīgi profesionālu apsvērumu dēļ. Pirms 1950. gada Latvijas lauksaimniecība vēl pārdzīvoja otrā pasaules kara sekas. Zemnieku saimniecības bija jau sagrautas, bet lielsaimniecības tikko izveidojās. Lauksaimniecības darba rezultāti tādos apstākļos nav uzskatāmi par raksturīgiem. Sākot ar 1990.g., lielsaimniecības nonāca krīzes apstākļos, un no jauna sāka izveidoties zemnieku saimniecības. Tādēļ sekojošie gadi ir raksturīgi ar vispārējai tendencei neatbilstošu graudaugu ražības samazināšanos. Pēdējo gadu datus uz iepriekšējo desmitgadu tendenču fona apspriedīsim nodaļas beigās.

Tātad kā sākotnējos datus izmantosim 14.10.tabulā parādīto dinamikas rindu 1950. - 1989. g. periodā.

Dinamikas rindas izvērtēšanu un apstrādi ir lietderīgi sākt ar grafisko attēlu, skat 14.5. attēlu

 

                                                                                                 14.10.tabula

Graudaugu ražība Latvijas visu kategoriju saimniecībās

 

Gads

1950

1951

1952

1953

1954

1955

1956

1957

1958

1959

1960

t        

1

2

3

4

5

6

7

8

9

10

11

Ražība

y

 

9.1

 

8.2

 

7.4

 

5.9

 

5.8

 

5.3

 

7.3

 

9.1

 

8.5

 

11.0

 

10.1

 

Gads

1961

1962

1963

1964

1965

1966

1967

1968

1969

1970

1971

t        

12

13

14

15

16

17

18

19

20

21

22

Ražība

y

8.6

7.3

7.2

11.9

15.2

11.9

16.3

18.0

20.8

23.1

26.3

 

Gads

1972

1973

1974

1975

1976

1977

1978

1979

1980

1981

1982

t        

23

24

25

26

27

28

29

30

31

32

33

Ražība

y

16.8

20.5

26.2

19.3

26.9

21.3

15.1

17.7

15.2

17.3

20.7

 

Gads

1983

1984

1985

1986

1987

1988

1989

t        

34

35

36

37

38

39

40

Ražība

y

20.7

26.7

22.1

25.1

29.9

21.5

28.1

 

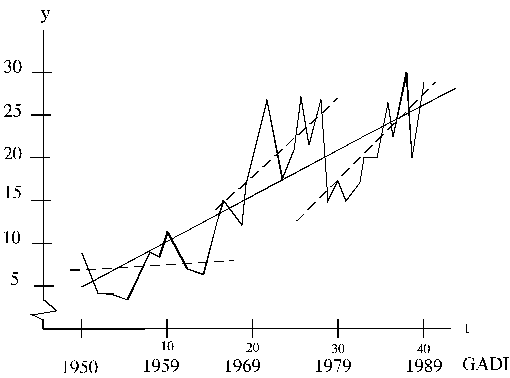
14.5. att. Graudaugu ražība Latvijas saimniecībās un lineāri trandi.

 

Pēc  14.5. attēla var vairāk vai mazāk pamatoti izvēlēties turpmākā darba metodes, paņēmienus un modeļus. Nesaistot aprēķinus ar grafisko analīzi, aprēķini lielā mērā kļūst formāli un viņu rezultāti mazcerīgi.

Jau pavirši aplūkojot attēlu, ir redzams, ka izmaiņas, šajā gadījumā - ražības pieaugums, neseko kādai vienai skaidri izteiktai tendencei. Bez tam ir vērojamas ļoti lielas svārstības gan ap vairāku gadu vidējiem, piemēram, iedomātiem slīdošajiem vidējiem, gan ap iedomātu trenda līniju.

Mēģinot visu 40 gadu periodu sadalīt raksturīgās daļās, veidojas šādi apakšperiodi.

Laika posms no 1950. līdz 1963. gadam. Ražība svārstās ap ļoti zemu vidējo līmeni; ražības pieaugums no gada uz gadu ir ļoti mazs. Lauksaimniecība tajā laikā atradās pilnīga panīkuma stāvoklī, jo bija citu tautsaimniecības nozaru neierobežotas ekspluatācijas objekts.

Laika posms no 1964. līdz 1972. gadam. Pateicoties lauksaimniecības produktu valsts iepirkuma cenu ievērojamam palielinājumam un valsts attieksmes pret lauksaimniecību būtiskām izmaiņām, vērojama vispārēja lauksaimniecības atveseļošanās, kas izpaudās arī ļoti straujā graudaugu ražības pieaugumā.

Tālākā laika posma periodizācija ir problemātiska. Ja aplūko visu 1973.- 1989.g. periodu vienkopus, tad to raksturo ļoti lielas ražības svārstības ap samērā augstu vidējo līmeni, kurš gan ievērojami atpaliek no attīstīto kaimiņvalstu (Zviedrijas, Dānijas, Somijas) rādītājiem.

Ja salīdzina savā starpā 1965.-1977. g. un 1978.-1989.g. periodus, abos ir novērojams gandrīz vienlīdz straujš ražības pieaugums. Bet neizskaidrots paliek lielais ražības kritums no 1976. g. līdz 1978.g. līmenim. Tikai šī atskaites bāzes samazināšanās rada šķietamību, ka ražības pieaugums rindas beigu daļā ir straujš; bez šī krituma pieaugums būtu niecīgs.

Tā kā apakšperiodu izdalīšana pēdējos 20 gados ir problemātiska un pārliecinoši to izdarīt nevar, turpmāk mēģināsim izdalīt visam 40 gadu periodam kopēju pamatizmaiņu trendu. Ja apakšperiodu izdalīšana būtu izdevusies pārliecinoša, kā pamatots altrernatīvs risinājums būtu pamattendences atklāšana un modelēšana katram apakšperiodam atsevišķi. Tādos gadījumos uzskata, ka visā dinamikas rindā nav vienas kopējas izmaiņu pamattendences, bet ir darbojušās dažādas tendences, jo ir bijuši atšķirīgi šīs tendences formējošie būtiskie faktori.

Ja izmaiņu pamattendences forma jeb veids nav skaidri izteikts un līdz ar to nav viegli noteikt, kāda matemātiska funkcija to vislabāk modelēs, darbu sāk ar lineāra trenda aprēķinu un taisnes iezīmēšanu diagrammā.

Izmantojot laika argumentus dabisko skaitļu veidā un vismazāko kvadrātu metodi pa visu dinamikas rindu iegūstam šādu lineāra trenda modeli:

 

                                                                                           (14.32)

 

Sakarības starp rindas līmeņiem un laika argumentu raksturo samērā  augsts korelācijas koeficients r =0,835. Pēc tā spriežot, varētu secināt, ka jau ir atrasts samērā labs trenda modelis. Atbilstošā taisne ir iezīmēta 14.5. attēlā; turpat ar pārtrauktām līnijām ir iezīmēti lineāri trendi pa trīs īsākiem periodiem atsevišķi. To lineāro trendu modeļi ir šādi.

 

1950.-1963.g. (t =1, ... , 14):                                              (14.33)

1964.-1976.g. (t=15, ..., 27):                                                  (14.34)

1977.-1989.g. (t=28, ..., 40):                                                  (14.35)

 

Spriežot pēc kopējā regresijas koeficienta, vidējais gada ražības pieaugums visa perioda ietvaros ir nedaudz vairāk kā 0,5 c/ha.

Ekonomikas rādītāju vispārēju uzlabošanos ilgstošā laika periodā pamato ar zinātniski tehnisko progresu. Runājot par graudaugu ražības pieaugumu, to nodrošina arvien uzlabota agrotehnika, ražīgāku šķirņu ieviešana, lielāku mēslojuma devu (līdz zināmai robežai) lietošana un citi pasākumi. Protams, zinātniski tehniskais progress nenoris vienmērīgi, tādēļ reālās dinamikas izpētei ir zinātniska un praktiska nozīme. Ražības novirzes no pamattendences rada galvenokārt atsevišķu gadu atšķirīgie meteoroloģiskie apstākļi. Ir iespējama arī īslaicīgu kā pozitīvu, tā negatīvu saimnieciska un kosmiska rakstura faktoru darbība.

Neskatoties uz samērā augstu sakarību ciešuma rādītāju, grafiskais attēls parāda, ka lineārs trends ļoti vienkāršo reālo ražības dinamiku, atspoguļojot vienīgi t.s.   ''gadsimta tendenci''. Tādēļ mēģināsim atrast citu modeli, kurš precīzāk aproksimētu faktisko dinamiku.

Ekonometrijā bieži ieteic izmantot funkcijas, kuras spēj aproksimēt izmaiņu īpatnības trīs dažādās dinamikas rindas daļās: pirmajā daļā - samērā mazus pieaugumus, kad notiek objekta jeb parādības sākotnēja formēšanās; otrajā daļā - strauju pieaugumu, kad notiek intensīva attīstība, bet trešajā daļā - dilstošus pieaugumus, kad objekts (parādība) tuvojas t.s. piesātinājuma stāvoklim. Runājot par ražību, šāds piesātinājuma stāvoklis šķiet ļoti loģisks, jo ražība kā sugu un šķirni raksturojoša īpašība nevar palielināties neierobežoti. Ja dinamikas rindai piemīt tādas īpašības (tās pamato ar profesionāliem apsvērumiem vai diagrammas vizuālu novērtēšanu), ekonometrijā kā piemērotu modeli ieteic loģistisko funkciju. Izdarot aprēķinus, šajā gadījumā loģistiskais modelis neattaisnojās¹.

 

 

 

 

 

________________________

1    Krastiņš O., Ciemiņa I. Dinamikas rindu modelēšana. R.: Latvijas statistikas institūts,
     1993 - 63 lpp.

14.4. 2. Ciklometriskais modelis

 

Par ciklometriskām sauc trigonometrisko funkciju  inversās funkcijas. Tās statistikas un ekonometrijas pētījumos līdz šim izmanto reti. Tomēr viņas sekmīgi var modelēt tāda pat rakstura dinamiku kā loģistiskā funkcija, turklāt ir daudz vienkāršāk  aprēķināmas.

Ja dinamikas rindas sākuma daļā ir vērojams mazs līmeņu pieaugums, vidusdaļā tas ir straujš, bet beigu daļā tuvojas piesātinājuma stāvoklim, tādu rindu var aproksimēt ar arktangensa funkciju, kura ir tangensa inversa funkcija:  Arktangensa funkcija eksistē visām reālām  x  vērtībām no  -līdz  . Funkcijas vērtības mainās no - 900 līdz + 900  jeb radiānos no - līdz . Funkcijas bezskalu grafiks parādīts 14.6. attēlā.

 

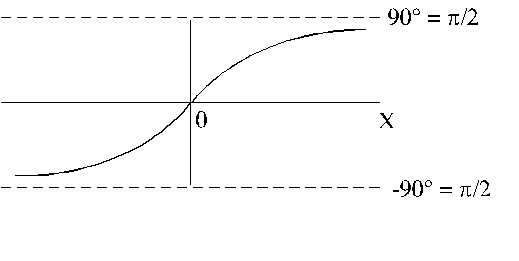
14.6. attēls. Arktangensa funkcijas bezskalu grafiks

 

14.11.tabula

Arktangensa funkcijas  vērtības

 

arc tgx

-¥

-1000

-5

-1

0

1

5

1000

¥

grādos

-90

-89,9

-79

-45

0

45

79

89,9

90

radiānos

-

-1,57

-1,37

-0,79

0

0,79

1,37

1,57

 

Lai arktangensa funkciju izmantotu dinamikas modelēšanā, modelī bez pašas šīs funkcijas ir vajadzīgi skaitliski parametri, kuri:

 

1) centrē līknes pārliekuma punktu  (x=o) pret to dinamikas rindas daļu, kur vērojams šāds izmaiņu raksturs: apzīmēsim šo parametru ar  l;

 

2) samēro arktangensa līknes trīs raksturīgās daļas (lēnu, strauju un atkal lēnu funkcijas augšanu) ar atbilstošām daļām dinamikas rindā; apzīmēsim šo parametru ar  k ;

 

3) samēro arktangensa līknes amplitūdu ar reālās rindas līmeņu amplitūdu; apzīmēsim šo parametru ar  b, jo to atradīsim kā regresijas koeficientu;

 

 4)  pārvieto arktangensa līkni pa vertikāli, paceļot to visā garumā pozitīvo y vērtību apgabalā, atbilstoši dinamikas rindas līmeņu vērtībām; apzīmēsim šo parametru ar  a, jo to atradīsm kā regresijas vienādojuma brīvo locekli.

 

Iestrādājot šos parametrus arktangensa funkcijā, iegūstam izmantojamo modeli vispārīgā veidā:

                                                y = a + b  arctg  k (t+ l).                                                         (14.36)

 

Parametrus  l un  k parasti nosaka kā apriorās konstantes ekspertīzes ceļā, bet  a un  b  aprēķina ar vismazāko kvadrātu metodi..

Kamēr uzkrājas vajadzīgā pieredze, aprioro konstanču noteikšanai ieteicams izgatavot arktangensa līknes skici, kurā ir parādītas vairākas savstarpēji atbilstošas abcisu ass skalas, skat. 14.7. att.

 

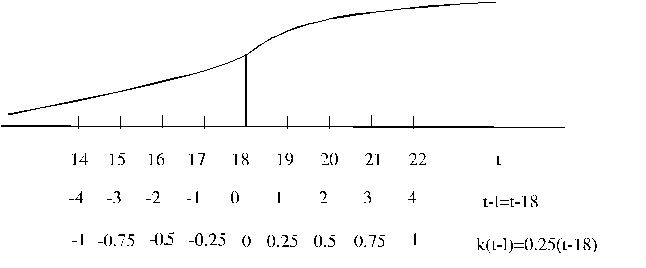
14.7.att. Arktangensa funkcijas argumentu pārveidojumi

 

Pēc apstrādājamo datu dinamikas rindas ekspertīzes ceļā nosakam, ka līknes pārliekuma punktam vajadzētu atbilst gadam ar kārtas skaitli  t =  18, līdz ar to konstante 1 = 18.

Arktangensa funkcija aug, argumentam  x  augot  no -1 līdz 1 ( pēc cita vērtējuma var teikt arī no - 1,5 līdz 1,5), tā tad divu vienību intervālā. Reālajā ražības dinamikā straujš pieaugums ir vērojams astoņu gadu laikā pa četriem gadiem abās pusēs no t = 18. Lai četras reizes izstieptu arktangensa līkni horizontālā virzienā, ir jāņem  k = 0,25. Pēdējo var aprēķināt arī kā attiecību starp to abcisu ass nogriezni uz  x  ass, kur līkne ir visvairāk izliekta, un gadu skaitu, kur ir noticis visstraujākais rindas līmeņu pieaugums.

 

Uzdevumā tas ir                       

 

Ievietojot apriori noteiktās konstantes arktangensa modelī, iegūstam               

                            

                                                 (14.37)

 

kuru linearizē, ņemot jaunu laika argumentu  z = arctg 0,25 ( t - 18 ).

 

 

 

Skaitļotāju var nostādīt darbam tiklab grādos, kā radiānos. Tikai šis pats nostādījums jāsaglabā, izmantojot modeli dinamikas rindas teorētisko līmeņu aprēķināšanai. Ir iespējams modelī paredzēt vēl vienu konstanti, ja notiek pāreja no grādiem uz radiāniem un otrādi, bet praksē tas nav vajadzīgs un sarežģī darbu. Turpmākie aprēķini ir izdarīti, uztverot arktangensa funkcijas argumentu grādos.

Izdarot aprēķinus ar vismazāko kvadrātu metodi pēc graudaugu ražības dinamikas rindas datiem 14.9. tabulas 2. un 3. rindas, iegūstam, ka b=0,1026; a=15,13; r = 0,886. Līdz ar to ciklometriskais ražības trenda modelis ir šāds:

                     

                                                                               (14.38)

 

Ar šo modeli izlīdzinātie ražības līmeņi ir parādīti 14.8. attēlā ar liektu, pārtrauktu līniju.

 

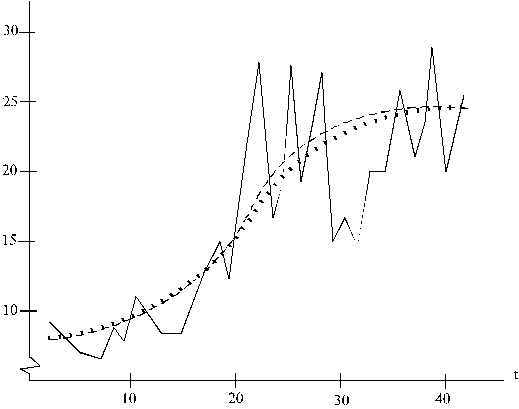
----- p=4; k= 0,25

 z  z  z  p=6; k= 0,1667

 

14.8.att. Graudaugu ražība un divi cikometriski trendi

 

Ciklometriskā līkne daudz labāk izlīdzina faktisko dinamiku nekā ar dažādiem  paņēmieniem aprēķinātas loģistiskās līknes, tāpat ir vērojamas priekšrocības, salīdzinot ar lineāru trendu.

Faktisko un izlīdzināto rindas līmeņu novirzes kompensējas (tuvojas nullei) atsevišķu apakšperiodu ietvaros. (skat. 12. tabulu), kas nozīmē, ka ciklometriskā līkne labi aproksimē faktiskos līmeņus visās rindas daļās. Noviržu kvadrātu summa gan lielākoties veidojas no pēdējo apakšperiodu saskaitāmajiem. To nevar vērtēt kā modeļa nepilnību, jo vienkārša vizuāla dinamikas rindas attēla apskate rāda, ka lielas, neregulāras ražības svārstības ir bijušas tieši pēdējā rindas daļā.

 

 

 

                                                                                             12. tabula

Faktiskās un ar ciklometrisko modeli izlīdzinātās graudaugu ražības novirzes un šo noviržu

kvadrāti pa dinamikas rindas daļām

 

Apakšperiodi

(gadu kārtas numuri)

 

 

 

  1. - 10.

- 0.1

23.6

11. - 20.

1.7

42.8

21. - 30.

1.6

          204.2

31. - 40.

- 2.7

          183.0

 

 

 

Pa visu dinamikas rindu

0.5

453.6

 

 

 

 

Atgriežoties pie apriorām konstantēm, var atzīmēt, ka parametru  l, kurš nosaka līknes novietojumu (centrējumu) laika skalā, parasti var noteikt samērā droši. Mazāk pārliecinošs ir parametra  k  vērtējums. Tiklab arktangensa līknes, kā arī reālās dinamikas rindas līknes galvenās (interesantākās, visvairāk izliektās) daļas jēdzieni ir izplūduši, un katrs izpildītājs tos var vērtēt citādi. Tādēļ, ja ir pieejams dators vai cits programmētās vadības skaitļotājs un līdz ar to atkārtoti aprēķini neprasa daudz pūļu, var izdarīt atkārtotu līknes parametru aprēķinu pie izmainītām  k  vērtībām.

 

Pieņemsim, ka ražības visstraujākais pieaugums ir bijis nevis 8, bet 12 gados, centrējot tos pret  t =18. Tādā gadījumā 

                                                  

 

Izdarot pārējo parametru aprēķinu ar vismazāko kvadrātu metodi, iegūstam  b = 0,116;
a =15,07;  r  = 0,880.

Tā kā abos gadījumos modeļiem ir viena un tā pati forma un minimizācijas nosacījumi ir saglabājušies, var salīdzināt abus korelācijas koeficientus. Pirmais no tiem ir lielāks. Izmainot parametru  k, aproksimācijas uzlabošanos neesam panākuši.

Pēc pēdējā modeļa aprēķinātās izlīdzinātās ražības ir ieskicētas 14.8. attēlā ar taisnstūrīšiem. Arī vizuāli vērtējot, šī līkne ražības izmaiņu tendenci neizsaka labāk kā agrāk aprēķinātā līkne, kura iezīmēta ar pārtrauktu līniju.

Var rasties jautājums, vai nav iespējams modelim (14.36) apriori noteikt parametrus  a un  b, lai tad ar vismazāko kvadrātu metodi aprēķinātu parametrus  k  un  l ? Sākonēji  šķiet, ka tas ir iespējams. Lai izdarītu vajadzīgo modeļa linearizāciju, parametri  a  un  b jāpārnes uz kreiso pusi un no abām pusēm jāņem tangensa funkcija 

 

                                                                                                               (14.39)

 

Apzīmējot   kl = A un  k= B, linearizācija ir pabeigta: z = A + Bt.

Tālāk seko grūtības, kuras konkrētajā gadījumā padara pārveidojumu neperspektīvu.

 

Tangensa funkcija pēc izliekuma rakstura atgādina arktangensa funkciju, pagrieztu par 90°, tai ir nevis horizontālas, bet vertikālas asimptotas. Apgabalā no  līdz     (pašos šajos punktos funkcijai ir asimptotas) tangensa funkcija strauji aug apgabala sākuma un beigu daļās, bet relatīvi lēni - centrālajā daļā. Tāda īpašība ir pilnīgi pretēja izlīdzināmās ražības dinamikas raksturam.

Bez tam, nosakot apriorās konstantes  a un b, bez visiem apsvērumiem jārūpējas,    lai       jo šajos punktos tangensa funkcija ir pārtraukta (tangensa argumentu interpretējot grādos).

 

Mēģinot izlīdzināt ražības dinamiku ar tangensa funkciju, ja apriorās konstantes būs noteiktas veiksmīgi, iegūsim modeli, kura grafiskais attēls ļoti tuvs taisnei. Tā kā arī lineārs modelis uzrādīja samērā augstu korelācijas koeficientu, tad samērā augstu korelācijas koeficientu uzrādīs arī tangensa modelis, radot ilūziju, ka tas samērā labi aproksimē faktisko dinamiku. Līdzīga aina vērojama daudzos gadījumos, ja izlīdzināšanai ir ņemta funkcija, kuras īpašības neatbilst faktisko datu dinamikas rindas raksturam.

Tādēļ modelis (14.38) ir jāatzīst par labāko savā grupā.

 

14.4.3. Periodisku  svārstību modelēšana

 

Otra dinamikas komponente (pēc pamattendences jeb trenda) ir periodiskas vai regulāras rindas līmeņu novirzes no trenda, ja konkrētajā dinamikas rindā tādas ir vērojamas. Periodiskās svārstības var atklāt vizuāli, aplūkojot dinamikas rindas un trenda līnijas grafisko attēlu.

Atgriežamies pie 14.5. attēla, kurā bija attēlota graudaugu ražības dinamika Latvijas saimniecībās un lineāri trendi. Viegli ievērot, ka faktiskā ražība nesvārstās ap trenda līniju haotiski, bet novirzes grupējas vairāk vai mazāk regulārās sērijās: vairākus gadus pēc kārtas novirzes no trenda ir vai nu pozitīvas vai negatīvas, pēc tam seko sērija ar pretēju zīmi. Ciklu garumu  un raksturu vieglāk novērtēt, izgatavojot jaunu grafisko attēlu, kur novirzes ir attēlotas, atliekot tās no horizontālās līnijas, skat. 14.9. attēlu. Brīvā interpretācijā var teikt, ka trenda taisne ( 14.5. att. ) ir pagriezta tā, lai viņa ieņem horizontālu stāvokli.

Ciklisko svārstību modelēšana vislabāk ir izpētīta, piemērojoties sezonālo svārstību pētīšanai. Šajā gadījumā plaši izmanto t.s.  harmonisko analīzi, ko aplūkojām iepriekš.

 

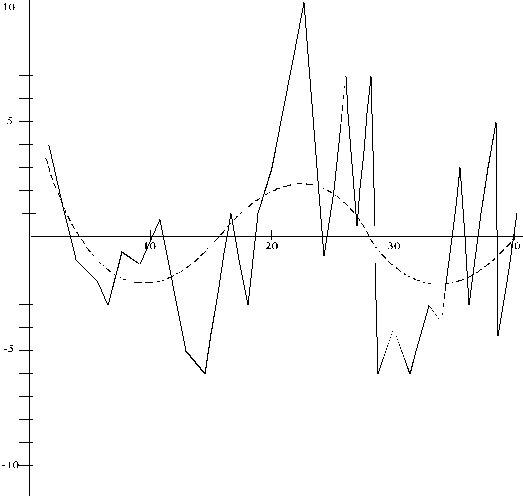
14.9. att. Faktiskās ražības novirzes no lineārā trenda un ciklisko svārstību sinusoīda

 

Pētījot un modelējot periodiskās svārstības, kurām nav sezonas raksturs un kuru vilnis  aptver vairākus gadus, universāls risinājums nav iespējams. Šajā gadījumā cikla garums ir  jāpamato patstāvīgi, un visvieglāk to izdarīt, izvērtējot grafisko attēlu.

Piemērojoties mūsu uzdevumam, modelēt graudaugu ražības noviržu no lineāra trenda periodiskās svārstības, izmantosim harmoniskās analīzes ( Furjē rindas ) pirmo sinusa komponenti. Tātad veidosim modeli;

 

                                                                                                   (14.40)

kur

       p -  cikla garums, piemērā - gados,  

       l -  cikla ekstremālās vērtības, piem., minimuma novirze no rindas sākuma,

      B -  koeficients, kurš raksturo viļņa aplitūdu,

      A -   modeļa brīvais loceklis, kurš, apstrādājot noviržu rindu, parasti ir tuvs

           nullei.                                                                                     

 

Parametrus  p  un  l  var noteikt kā aprioras konstantes, rūpīgi izvērtējot grafisko attēlu. Parametrus  A  un  B  aprēķina ar vismazāko kvadrātu metodi.

 

Lai novērtētu parametrus  p  un  l izstrādātajam graudaugu ražības noviržu no trenda modelim, atgriežamies pie 14.9. attēla. Mēģināsim vizuāli uzzīmēt sinusoīdu (nepretendējot uz pareizu amplitūdu), kura vislabāk aproksimētu reālo dinamiku. Šajā darbā svarīgi ievērot, lai visi viļņi (pozitīvie un negatīvie) būtu viena garuma un to ekstremālās vērtības visumā atbilstu vislielākajām faktiskās dinamikas novirzēm.

Šīs līknes īpašības turpmākie aprēķini precizēt nevarēs, tāpēc darbs jāveic ar maksimālu rūpību.

Pēc 14.9. attēla redzams, ka cikla pozitīvie un negatīvie viļņi tuvināti noslēdzas 12 gados. Tātad pilns cikla garums varētu būt 24 gadi. To pieņemam par parametru  p, līdz ar to varam aprēķināt parametru  k:

                                                   

 

Tālāk jāaprēķina parametrs  l,  kas nostāda sinusoīdas fāzi atbilstoši faktisko datu svārstību fāzei.

Līknes pirmais minimums ir jāvērtē starp 9. un 10. gadu, tātad  ja  t = 9,5. Zinot, ka  sinusa funkcijas minimums ir    var sastādīt un atrisināt vienādojumu

 

                              sin 15 (9,5 + l) = sin 270;

                                    15 (9,5 + l) =270 ;     

                                                     l = 8,5.

 

Līdz ar to esam ieguvuši modeli

 

                                                                                                     (14.41)

 

kura parametrus  A  un  B  var atrast ar vismazāko kvadrātu metodi, pieņemot, ka  z = sin 15 (t+8,5). Par sākotnējo informāciju jāizmanto novirzes   

Laika argumenta pārveidojumu izdara ar nelielu apkašprogrammu, kuru pievieno dinamikas rindas vai korelācijas regresijas tipveida programmai.

Izdarot vjadzīgos aprēķinus, iegūstam, ka  B = 3,629; A = 0,579;  r =0,633.

Modelis ir šāds: 

                                                                                          (14.42)

 

Parametrs 3,623, kā jau bija minēts, nosaka, sinusoīdas amplitūdas lielumu. Nedaudz gūtāka ir parametra 0,579 interpretācija. Formāli tas raksturo sinusoīdas vertikālo nobīdi pret abcisu asi. Piemērā sinusoīdas horizontālās simetrijas ass ir aptuveni  0,6  vienības virs abcisu ass. Parasti parametrs ir tuvs nullei. Vairāk no nulles tas atšķiras tad, ja faktisko datu novirzes no trenda sadalās tā, ka pa vienu pusi ir lielāks noviržu skaits, bet pa otru - novirzes ar lielāku absolūto vērtību.

Zīmējot sinusoīdu, parametru  0,579  var neņemt vērā. Tad līkne precīzi krustos abcisu asi ar apriorajām konstantēm noteiktajos punktos. Izdarot izlīdzināto noviržu aprēķināšanu, jāņem vērā abi parametri.

Trigonometriskais modelis (14.42) fiksē vidēji ciešas ražības noviržu no lineārā trenda sakarības ar modificēto laika argumentu ( r = 0,623). Katrā ziņā tas ir jāņem vērā, raksturojot reālās dinamikas īpatnības.

Ražības ciklisko svārstību cēloņi pagaidām nav pilnīgi noskaidroti. Literatūrā ir vairākkārt norādīts, ka visu dzīvo dabu ietekmē saules aktivitātes cikli, kuru garums ir 7 un 11 gadi. Saules aktivitāti parasti raksturo t.s. Volfa skaitļi. Mūsu mēģinājumi atrast korelatīvu sakaru starp ražības novirzēm no trenda un Volfa skaitļiem pagaidām pārliecinošus rezultātus nav devuši. Tomēr citi autori, izmantojot pagājušā gadsimta datus, tādas sakarības ir konstatējuši.

 

14.4.4. Lineāra trenda un periodisku svārstību modeļi

 

Ražības dinamikas precīzākai raksturošanai ir lietderīgi apvienot trenda modeli ar periodisko svārstību modeli. To var darīt tad, ja otrajā modelī par rezultatīvo pazīmi neņem pašus rindas līmeņus, bet gan to novirzes no trenda. Ja gadījumā būtu korelācija starp abu modeļu argumentiem, tad, šādi rīkojoties, abu argumentu kopietekme tiktu izsmelta ar pirmo modeli kā galveno. Uzdevuma ietvaros abu modeļu arguments ir līmeņu secības koeficients: pirmajā modelī tiešā veidā  t, otrajā kā trigonometrisks pārveidojums sin15 ( t+ 8,5 ).Garā dinamikas rindā, kura aptver daudzus trigonometriskās funkcijas viļņus, šie lielumi praktiski nekorelē. Īsā rindā, kurā ir tikai viens divi viļņi, vai to daļas, zināmu korelāciju izraisa tas, kāda cikla fāze ( pozitīvā vai negatīvā ) ir rindas sākumā un kāda - beigās. Tas iepriekš aprādīto apsvērumu dēļ nav šķērslis abu modeļu apvienošanai vienā, tos saskaitot. Tomēr nedrīkst saskaitīt abu modeļu determinācijas koeficientus, jo zināmas korelativitātes gadījumā summa var būt lielāka par vienu, kas jāvērtē kā loģiska kļūda. Apzīmējot    varam rakstīt, ka

 

Saskaitot brīvos locekļus un noapaļojot parametrus līdz sākotnējo datu precizitātei, iegūstam:

 

                                                                               (14.43)

 

Ar pēdējo modeli aprēķinātā (izlīdzinātā) līkne ir parādīta 14.10. grafiskajā atēlā kā augšupejoša sinusoidāla līkne. Ir redzams, ka šī līkne daudz labāk nekā taisne izlīdzina faktisko datu dinamiku (lauzto līniju).

 

 

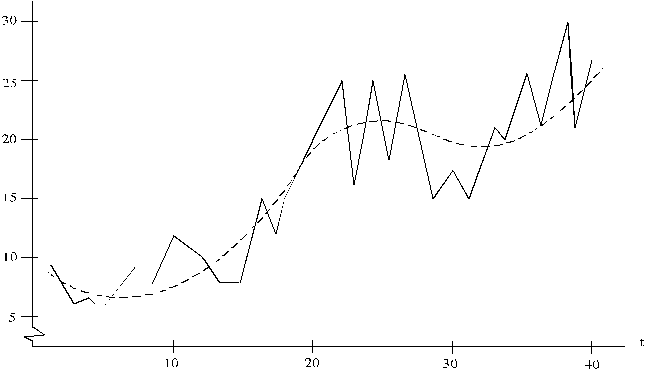
14.10.att. Graudaugu ražība Latvijā un kombinētā lineārā trenda un viena perioda
svārstību līnija 

 

Par pakāpenisku izlīdzināšanas kvalitātes uzlabošanos labi var spriest pēc tā, ka samazinās neizskaidrotā noviržu kvadrātu summa. Par bāzi jāizmanto kopējā noviržu kvarātu summa  Lineārā trenda modeļa neizskaidrotā noviržu kvadrātu summa ir   Kombinētā modeļa neizskaidrotā noviržu kvadrātu summa ir: 

Izejot no noviržu kvadrātu summām, var aprēķināt arī kombinētā modeļa korelācijas koeficientu (indeksu). Tas jāaprēķina, izmantojot korelācijas attiecības formulu:

 

                                        

 

Lineārā trenda korelācijas koeficients bija  0,853.  Tātad, pievienojot modelim ciklisko komponenti, ir diezgan ievērojami uzlabota reālās dinamikas aproksimācija.

Periodisko svārstību izpēti var turpināt, vēlreiz atkārtojot iepriekš veiktos darba soļus. Izskaitļo faktiskās ražības novirzes no aprēķinātās ar kombinēto trenda -  svārstību modeli. Tās ir attēlotas 14.11. attēlā

 

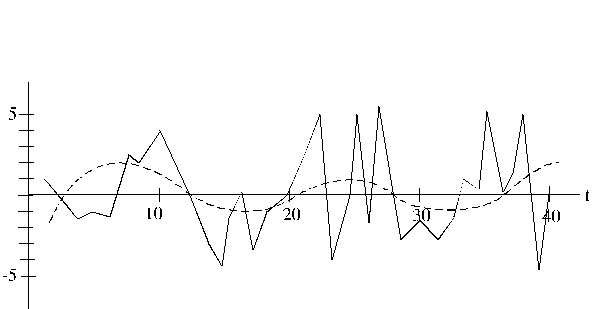
14.11.att. Faktiskās ražības novirzes no kombinētā lineārā un

viena perioda svārstību trenda.

Izdalīta otra īsāka perioda izlīdzinoša sinusoīda.

 

Pēc šī attēla var izdalīt īsāku svārstību vilni, kura viens vilnis aptver 8, bet viss cikls 16 gadus. Līdz ar to nākošajā svārstību modelī  p = 16. Pozitīvā viļņa virsotne jācentrē pret 8. gadu, kuram jāpiekārto , jo   un ir maksimāls. Tādējādi

 

                                                          ,

no kurienes  l = - 4. Līdz ar to, izmantojot vismazāko kvadrātu metodi,  ir jāaprēķina modeļa   parametri:

                                                                                                 (14.44)

 

Izdarot izskaitļojumus, iegūstam, ka  ,   un  r=0,338.

Modelis ar noapaļotām konstantēm būs šāds:

 

                                                 .                                   (14.45)

 

Pievienojot šo komponenti kombinētajam trenda - periodisko svārstību modelim (14.43), iegūstam

,               (14.46)

 

pēc kura atkal var aprēķināt teorētiskās jeb izlīdzinātās ražības un izgatavot jaunu grafisko attēlu (14.12. att.).  

 

Kombinētā lineārā trenda un divu periodu cikliska svārstību modeļa sakarību ciešuma rādītājs

 

 

norāda uz ļoti labu aproksimāciju. To apstiprina arī  14.12. grafiskais attēls.

 

 

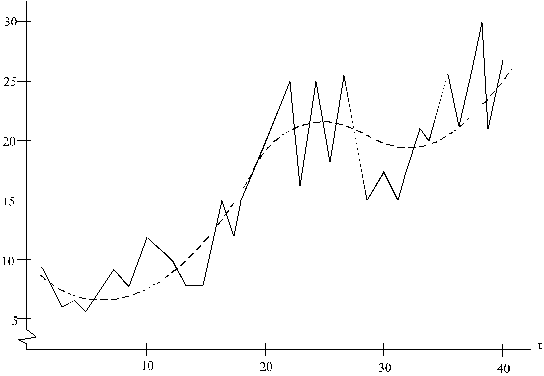
14.12.att. Graudaugu ražība Latvijā un kombinēta lineārā trenda un divu periodu svārstību līnija

 

 

 

 

 

 

 

 

14.4.5. Ciklometriska trenda un periodisku svārstību modelis

 

Ņemot vērā, ka lineārs trends izsaka ražības izmaiņas pamattendenci tikai pašā vispārīgākā veidā, var rasties vēlēšanās periodisko svārstību modeli apvienot ar kādu citu trendu. Iepriekš kā samērā pamatots bija novērtēts ciklometrisks trends, kuru aproksimēja paplašināta arktangensa funkcija. Tādēļ pārbaudīsim, kā reālo graudaugu ražības dinamiku apraksta ciklometriskais trenda modelis, ja to apvieno ar periodisko svārstību modeli. Pēdējam atkal izmantosim paplašinātu sīnusa funkciju.

Svārstību perioda ilgumu un viļņa centrējumu var ņemt tādus pašus kā iepriekš, bet var novērtēt un pamatot no jauna. Tā kā iepriekš noteiktajiem periodiem cēlonisks pamatojums vēl nav atrasts, aprioro konstanču noteikšanu izskatīsum no jauna.

Šajā nolūkā, izmantojot faktisko ražību novirzes no izlīdzinātajām saskaņā ar ciklometrisko trendu, ir jāizgatavo grafiskais attēls, skat. 13. attēla augšējo daļu. 

 

 

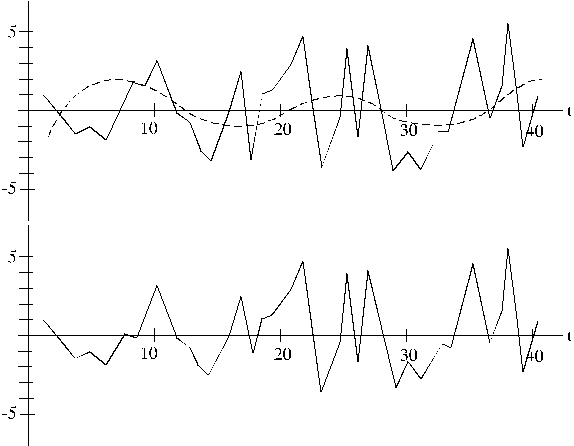
14.13.att. Ražības novirzes  no ciklometriskā trenda  un ciklisko svārstību līkne (augšējā
                diagramma);  ražības novirzes no kombinētā ciklometriskā trenda (apakšējā diagramma)

 

Vadoties galvenokārt pēc pēdējo 20 gadu datiem, kur novirzes ir vislielākās un kuras modelēt vajadzētu vispirms, var ievērot, ka pozitīvo noviržu vilni nomaina negatīvo noviržu vilnis pēc 9 gadiem. Līdz ar to pilna cikla ilgumu var pieņemt 18 gadi. Šāds periods un viņa fāze atbilst arī otrajam gadu desmitam izmantotajā laika posmā, bet svārstību fāze ir pretrunīga pirmā gadu desmita novirzēm.

Piemeklēt ciklu, kurš gan pēc garuma, gan fāzēm ideāli atbilstu visu 40 gadu ražības dinamikai, ir grūti. Tādēļ ņemot vērā, ka pirmajā gadu desmitā novirzes ir mazas un dinamikas pētījumos senākos gadus vērtē kā mazāk informatīvus kopējā tendeņču formēšanā, izmantosim 18 gadu periodu ar minimumiem 14. un 32. gados.

Vadoties no grafiskās analīzes, var noteikt periodisko svārstību modeļa apriorās konstantes:  p= 18;   20 (14+l)=270, no kā seko, ka l = -0,5.Ar vismazāko kvadrātu metodi ir jāaprēķina modeļa

 

                                                                                                     (14.47)

parametri  Aun B, izmantojot  kā sākotnējo informāciju faktiskās ražības novirzes no aprēķinātajām. Pēdējās aprēķina izmantojot ciklometrisko trendu.

 

Aprēķinu rezultātā iegūstam, ka  A=-0,1016 (sagaidāms tuvu nullei), B=1,918 (formē sinusoīdas amlitūdu) un  r = 0,399 (raksturo sakarību ciešumu). Iegūtais modelis ar noapaļotiem parametriem ir šāds:

                   

                                                                                      (14.48)

 

Izmantojot 24 gadu garu ciklu un centrējot to tāpat, kā modelējot noviržu un lineāra trenda dinamiku, iegūstam:

 

                                        (14.49)

 

Tā sakarību ciešuma rādītājs ar laika argumentu  r = 0,365 ir nedaudz zemāks nekā modelim (14.48).

 

Savukārt,  modelējot novirzes no lineāra trenda ar 18 gadu periodu, centrētu kā modelim (14.47),  iegūstam:

 

                                   (14.50)

 

kura sakarību ciešuma rādītājs  r = 0,501 ir ievērojami zemāks nekā modelim (14.42).

 

Tātad ciklisko svārstību periods un tā centrējums šķietami ir atkarīgs no tā, kādu trenda modeli profesionāli vērtējam kā pareizāku. Kamēr nav samērā droši noskaidrots ciklisko svārstību cēlonis, katru no trenda modeļiem var apvienot ar  to ciklisko svārstību modeli, kurš vislabāk apraksta atlikušo variāciju.

Apvienojot modeli (14.48) ar ciklometriskā trenda modeli (14.38), iegūstam:

 

                (14.51)

 

Ar pēdējo modeli aprēķinātās izlīdzinātās graudaugu ražības ir parādītas 14.13. tabulā, bet modeļa attēls (līkne) uz faktiskās ražības dinamikas fona - 14.14 attēlā. Līkne visumā labi seko faktisko rindas līmeņu  izmaiņu īpatnībām, ja neskaita pirmos 7 gadus, kur līkne un faktiskā dinamika ir '' pretfāzēs ''.

 

 

 

 

 

 

 

 

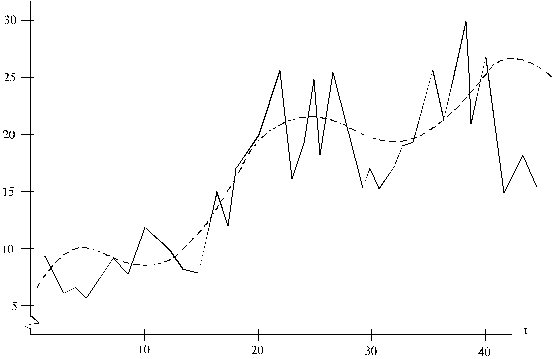
14.14.att. Graudaugu ražība Latvijā un kombinētā ciklometriskā trenda

un viena perioda svārstību līnija

     

 

Faktiskās ražības novirzes no izlīdzinātās ar kombinēto modeli ir parādītas 14.13. grafiskā attēla apakšējā daļā. Novērtējot šo attēlu kopumā, jāsecina, ka periodisko svārstību uztveršana modelī ir vienīgi samazinājusi atlikušās novirzes, bet nav izmainījusi to izmaiņu kopainu. Atsevišķos gados faktiskās ražības līmeņi ir tik lieli, bet citos tik mazi, ka tos acīmredzot nekādi nevar izskaidrot ar kādu visam 40 gadu periodam raksturīgu pamattendenci vai ar periodiskām svārstībām. Teikto vēl pastiprina minētā attēla salīdzinājums ar 14.12. attēlu, kur izlīdzināšanas pamatā bija lineārs trends.

                                                                                                     13. tabula

Faktiskā un ar kombinēto metodi aprēķinātā graudaugu ražība Latvijā

 

Gads

1950

1951

1952

1953

1954

1955

1956

1957

1958

1959

Faktiskā y

9,1

8,2

7,4

5,9

5,8

5,3

7,3

9,1

8,5

11,0

Izlīdzinātā 

7,5

8,2

8,8

9,2

9,5

9,5

9,3

9,0

8,6

8,2

1,6

0,0

-1,4

-3,3

-3,7

-4,2

-2,0

0,1

-0,1

2,8

 

Gads

1960

1961

1962

1963

1964

1965

1966

1967

1968

1969

1970

Faktiskā y

10,1

8,6

7,3

7,2

11,9

15,2

11,9

16,3

18,0

20,8

23,1

Izlīdzinātā 

7,9

7,8

8,0

8,5

9,4

10,8

12,6

14,7

16,8

18,7

20,3

2,2

0,8

-0,7

-1,3

2,5

4,4

-0,7

1,6

1,2

2,1

2,8

 

 

 

 

13. tabulas turpinājums

 

Faktiskā un ar kombinēto metodi aprēķinātā graudaugu ražība Latvijā

 

Gads

1971

1972

1973

1974

1975

1976

1977

1978

1979

1980

1981

Faktiskā y

26,3

16,8

20,5

26,2

19,3

26,9

21,3

15,1

17,7

15,2

17,3

Izlīdzinātā 

21,4

22,2

22,6

22,7

22,5

22,1

21,7

21,3

20,9

20,7

20,7

4,9

-5,4

-2,1

3,3

-3,2

4,8

-0,4

-6,2

-3,2

-5,5

-3,4

 

Gads

1982

1983

1984

1985

1986

1987

1988

1989

1990

1991

1992

Faktiskā y

20,7

20,7

26,7

22,1

25,1

29,9

21,5

28,1

23,6

20,3

16,4

Izlīdzinātā 

20,9

21,4

21,9

22,6

23,4

24,1

24,6

25,0

25,2

25,1

24,8

-0,2

-0,7

4,8

-0,5

1,7

5,8

-3,1

3,1

-1,6

-4,8

-8,4

 

Gads

1993

1994

1995

1996

1997

1998

1999

2000

2001

Faktiskā y

17,7

18,4

16,9

 

 

 

 

 

 

Izlīdzinātā 

24,3

23,7

23,1

22,5

22,0

21,7

21,6

21,8

22,1

-6,6

-5,3

-6,2

 

 

 

 

 

 

 

Rindas laika argumentu un graudaugu ražības sakarību ciešuma rādītāju, aproksimējot sakarības ar pēdējo kombinēto modeli (14.51), var aprēķināt pēc atlikušajām novirzēm un izmantojot korelācijas attiecības formulu

 

 

Atbilstošs sakarību ciešuma rādītājs, aproksimējot sakarības ar lineāru trendu un vienu trigonometrisku vilni, bija 0,915, bet, ņemot vērā divus trigonometriskus viļņus, - 0,926. Šie rādītāji ir savā starpā salīdzināmi, jo ir aprēķināti tieši pēc rindas faktisko un izlīdzināto līmeņu novirzēm, bet nevis pēc kādiem sākotnējo datu pārveidojumiem. Pēc sakarību ciešuma rādītājiem vērtējot, lineārs trends kopā ar ciklisko svārstību modeli sasniedz nedaudz labāku aproksimāciju.

Varētu mēģināt arī ciklometrisko trendu kombinēt nevis ar viena, bet divu trigonometrisko viļņu modeļiem. Tomēr tāda rīcība var novest jau pie diezgan formāliem rezultātiem, jo modeļa parametru un aprioro konstanču skaits kļūst liels. Pēdējā kombinētajā modelī to ir 7, bet kombinētajā lineāra trenda un divu trigonometrisko viļņu modelī (14.46) - 8. Pievienojot modelim (14.51) vēl vienu trigonometrisko komponenti, parametru un aprioro konstanču skaits būtu 9. Ir zināms, ka, šādu procesu turpinot tiktāl, kamēr modeļa parametru skaits sasniedz novērojumu skaitu, var panākt, ka modeļa līkne precīzi atkārto visus sākotnējo datu līmeņus. Tātad par kādu tendences vai periodisko svārstību izdalīšanu vairs nav runa. Tādēļ regresijas analīzē pieņem, ka novērojamu skaitam ir jābūt apmēram 10 reizes lielākam nekā izvēlētā modeļa parametru skaitam, un arī tad parasti novērojumu ir par maz, un parametru statistiskā nozīmība zema. Izlīdzinot dinamikas rindas, šī prasība nav tik stingra, jo laika arguments (vienīgā reālā faktora) matemātiskos pārveidojumus cenšas izvēlēties tā, lai tie maz korelē savā starpā. Un tomēr rindas līmeņu skaitam vajadzētu būt vismaz 5 reizes lielākam nekā modeļa parametru un aprioro konstanču skaitam.

 

Tādēļ graudaugu ražības dinamikas modeļu meklējumi ir jābeidz.Esam pilnīgāk vai virspusējāk raksturojuši izstrādāto modeļu priekšrocības un trūkumus. Galīgo izvēli atstājam tālākiem pētījumiem, jo mūsu mērķis nebija dot gatavas receptes, bet veicināt zinātniskās domāšanas procesu.

Nobeigumā varam izrēķināt, izmantojot (14.51) modeli, teorētiskās ražības arī ekstrapolācijas apgabalam - 1990. - 2001. gadu periodam. Tas ir izdarīts 14.13. tabulas beigās un daļa rezultātu parādīta arī 14.14. attēlā.

Kā jau tas bija sagaidāms, faktiskās ražības  1990. - 1995. g. periodā bija daudz zemākas. Trendu un ciklisko svārstību modeļi nespēj prognozēt katastrofas dabā un revolucionāras izmaiņas ekonomikā. Tie, aprakstot faktisko dinamiku, var dot zināmus prognožu vērtējumus tikai tad, ja izmaiņas ir evolucionāras.

Tātad modeļu izvērtēšana ir jāveic kompleksi, izmantojot gan matemātiskus, gan profesionālus (nematemātiskus) kritērijus un apsvērumus. Turklāt pēdējiem parasti ir izšķiroša nozīme.

Līdz ar to rodas nepieciešamība saskaņoti attīstīt matemātisko instrumentāriju un profesionālās argumentācijas metodiku. Novērtējot patreizējo zinātnes attīstības gaitu, ir redzams, ka matemātiskā instrumentārija attīstība strauji apsteidz loģiski profesionālo argumentāciju šī instrumentārija lietošanai.

Tādēļ apsteidzošos tempos ir jāattīsta robežzinātnes, kuras saista matemātiku, t.sk. matemātisko statistiku, ja to saprot kā matemātikas daļu, ar profesionālām zinātnēm, mūsu gadījumā, ar ekonomiku, kuru ietvaros matemātiku vajadzētu pielietot. To cenšas darīt robežzinātne ekonometrija.